Diapositiva 1 - Dipartimento di Scienze Matematiche, Fisiche e

UNIVERSITÀ
DEGLI STUDI
DI PARMA
Corso di laurea Magistrale in Fisica
Insegnamento: Materiali Nanostrutturati di Carbonio
Francesco Cugini
15 maggio 2012

introduzione
 perché studiare il magnetismo nel carbonio?


storia magneti molecolari
magnetismo nel carbonio
 evidenze sperimentali
▪ fullereni
▪ grafite
 modelli teorici
“If confirmed, carbon magnetism,
will be a breakthrough
in material science”
F.Palacio, Nature 2001

applicazioni tecnologiche
 magneti non metallici
▪
▪
▪
▪
leggeri
economici
isolanti elettrici
biocompatibili
 spintronica
▪ data storage
▪ comunicazioni e processi
veloci e a basso consumo
energetico

interesse accademico
 magnetismo orbitali p e s
 ampio dibattito
▪ previsioni teoriche
▪ poca riproducibilità
 nuove scoperte:
▪ grafene






fisica
chimica, biochimica
scienze materiali
geologia, cosmologia
ingegneria
medicina

fine anni ’60:
 prime ipotesi magnetismo composti organici

1972:
 primo ferromagnete molecolare

1986:
 scoperta ferromagnetismo p – electrons
 magneti metal-free → TC bassissime

anni ’90 :
 primi magneti organici a T ambiente
→ presenza atomi metallici

sfida: magneti molecolari
 composti solo da elementi leggeri
 alte Tc
M(TCNE)
J. M. Manriquez et al.
Science, 252 (1991) 1415

anni ’90 :
 primi magneti organici composti solo elementi leggeri
→ basse Tc
p- nitrophenyl
nitronyl nitroxide
tetrakis (dimethylamin)
ethylene – C60
Tc= 0.65K
Tc= 16,1 K
Takahashi et al, Phys. Rev. Let. 1991
P.M. Allemand, et al. Science, 1991.


difficoltà → metal-free + alte Tc
varie osservazioni di debole spontanea
magnetizzazione a T > ambiente
▪ segnali molto deboli e irriproducibili

1996
“Of many candidates of the magnets, carbon compounds will be the most
promising from the practical point of view, because the carbons exhibit a
spontaneous magnetization at room temperature and are cheap to make,
chemically and physically stable, and easy to process.”
K. Murata and H. Ushijima. J. of NIMC. 4 (1996) 1.

Modelli teorici
 prevedono ferromagnetismo legato a
difetti

anni 2000 → evidenze sperimentali in:
 Rh – C60 (Makarova et al., Nature, 2001)
 HOPG (Kopelevich, J.L. T. Phys. 2000)
 nanoschiume, film sottili, nanodiamanti

dubbi:
 segnali molto deboli
 impurezze
 poca riproducibilità

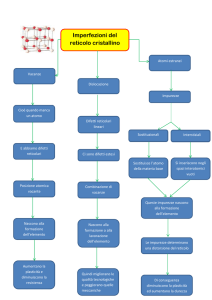
C60 Buckminster-fullerene

Cristallo: reticolo cubico fcc con alto
impacchettamento


forze Van der Walls
comportamento diamagnetico
Polimerizzazione in strutture 1D, 2D, 3D
meccanismi di polimerizzazione:


▪ [2+2] cicloaddizione
▪ C-C singolo legame covalente

Indotta da:
▪ alte T e alte P
▪ eccitazione con luce
▪ collisione con molecole

legami controllati con elementi intercalati

Rh-C60
C60 Romboedrico
 ottenuto con trattamenti ad alte T (1000K) e alte P (4GPa) di C60 puro
2001 : evidenze sperimentali:
“strong magnetic signals in rhombohedral C60”

(Makarova et al, Nature, 2001)

sintesi:
 6 Gpa
 ~ 1000 K

caratterizzazione della
struttura:
 spettroscopia Raman
 diffrazione raggi X
 SEM (scanning electron
Spettro Raman Rh-C60
microscope)
(Makarova et al, Nature, 2001)

SQUID (superconducting quantum interference device)
 magnetometro ad estrazione
 basato effetto Josephson quantistico
 sensibilità 10-7 emu

misure magnometria SQUID
 fase ferromagnetica
▪ ciclo isteresi
▪ magnetizzazione di saturazione
▪ Tc ~ 500K
Δ T=10K
• T=300K
(Makarova et al, Nature, 2001)

ipotesi per spiegare effetto:
 impurezze → non sono sufficienti
 cicloaddizione [2+2]
→ re-ibridizzazione sp2 -sp3
 difetti topologici → gap nella densità di stati

dubbi
 segnale debole
 impurezze
 riproducibilità → forte legame condizioni
sintesi
 vicinanza alla T di rottura della struttura
(Makarova et al, Nature, 2001)

2006
ritrattazione articolo
 FM creato dalla
cementite Fe3C
 C60 puro non è
ferromagnetico

anni seguenti tentati:
 vari metodi e condizioni sintesi
 intercalazione atomi leggeri
 Nessun Ferromagnetismo
stabile a T ambiente è stato
provato
Li4C60

Grafite




struttura planare esagonale
ibridizzazione orbitali sp2
delocalizzazione legame π lungo l’anello
impacchettamento piani
▪ esagonale
▪ rombroedrico
 non esiste cristallo monocristallino
macroscopico

HOPG (Highly Ordered Pyrolytic Graphite)

deposizione pirolitica
 alto grado orientazione preferenziale piani

materiale DIAMAGNETICO

elettroni p delocalizzati
 elevato lungo c

previsioni teoriche:

Ferromagnetismo e Superconduttività nei pressi di difetti topologici dei piani di grafite
 Ferrimagnetismo negli stati di bordo dei piani di grafene

2000: prime evidenze sperimentali FM e SC
cicli di isteresi con H parallelo ai piani
indipendente V proprietà bulk
 ruolo impurezze?
cicli di isteresi con H perpendicolare piani
(Kopelevich et al, J.L. T. Phys. 2000)

Verifica correlazione magnetizzazione – impurezze in:
 HOPG varia provenienza
 Grafite Kish
 Grafite Naturale



misure magnetiche → SQUID
cristallinità campioni → diffrazione raggi X
concentrazione impurezze → PIXE
(Esquinazi, Phys. Rev. B, 2002)

PIXE (Particle-induced X-ray emission)

fascio di protoni 2 MeV
interazione atomica
emissione raggi X caratteristici elemento



ciclo d’isteresi anche a T ambiente

no correlazione tra magnetizzazione
(e campo coercitivo) e quantità di
impuerezze

impurezze non sono causa
ferromagnetismo in HOPG e Kish
(Esquinazi, Phys. Rev. B, 2002)
•
•

controllo
impurezze PIXE
durante
irraggiamento
caratterizzati da
AFM e MFM dopo
irraggiamento
HOPG IRRAGGIATA
▪ impurezze < 1 ppm
▪ irraggiata fascio protoni 2.25 MeV
▪ 4 stage
1.
2.
3.
4.
(Esquinazi, Phys. Rev. Let., 2003)
omogenea , carica totale 2.93 μC
spot al centro, carica totale 8 μC
4 spot, carica totale 600 μC
uguale a 3 ma con corrente di protoni
minore

magnetic moment (10-6 emu)

carattere FM aumenta con carica irraggiata
ms ~ Ct1/2
(Esquinazi, Phys. Rev. Let., 2003)

conclusioni lavoro HOPG irraggiata:
 ordine FM stabile a T ambiente
▪ possibilità creazione spot micrometrici FM attivi
 bassa anisotropia (tra H parall e perpend piani)
 carattere FM cresce con carica irraggiata
 bombardamento con He no carattere FM
▪ importanza H nella struttura grafite
(Esquinazi, Phys. Rev. Let., 2003)
Negli anni seguenti…

Conferme sperimentali…  Spiegazioni teoriche…
 in HOPG pura
 in HOPG irraggiata
▪
▪
▪
▪
▪
misure SQUID
AMR
AFM, MFM e EFM
XMCD
LEμSR
▪
▪
▪
▪
difetti
bordi
bordi di grano
ruolo idrogeno

Andamento lineare della magnetizzazione di
un HOPG irraggiata
 accordo con modello
Heisemberg 2D
 stesso comportamento
lineare nella grafite
vergine
 esclusa causa impurezze
 sottratto contributo
prima dell’irraggiamento
(Barzola-Quiquia, Phys. Rev. B, 2007)

Magnetoresistenza

variazione R in funzione del campo applicato

magnetoresistenza anisotropa

utile per campioni sottili

nella grafite irraggiata:
▪
▪
anisotropia
isteresi FM



AFM (Atomic Force Microscopy)
MFM (Magnetic Force Microscopy)
EFM (Electric Force Microscopy)

indagine microscopica
 AFM (a)
 MFM (b,c)
 EFM (d)
▪ A no segnale magnetico
▪ B,C no segno topologico
▪ carattere FM
(Cervenka, Nature, 2009)

Bordi di grano
 legati crescita cristallo
 array 2D difetti
 STS si creano stati
localizzati
• possibile causa FM?
(Cervenka, Nature, 2009)

X-Ray Magnetic Circular
Dichroism
 dicroismo circolare: diverso
assorbimento della luce polarizzata
circolarmente
 STXM microscopio a trasmissione
 cambiando energia raggi X
▪ picco risonanza dipende
▪ composizione
▪ struttura elettronica
 variando polarizzazione
▪ informazioni magnetiche
▪ intensità trasmessa
▪ angolo tra momento magnetico e segno
polarizzazione
(immagini STXM con diverse polarizzazioni
raggi X e diverse orientazioni del campo)
(Spettro assorbimento di 2
campioni preparata T diverse)
(Ohldag, Phys. Rev. Let., 2007)

XMCD
 con irraggiamento si crea ordine ferromagnetico
 originato dalla polarizzazione degli spin degli
elettroni π del carbonio
 campioni ri-grafitizzati
▪ momento magnetico maggiore
(Ohldag, Phys. Rev. Let., 2007)

sonda locale magnetica (sensibilità momenti: 10-4μb)

muoni polarizzati impiantati nel campione
 creati dal decadimento di π+
 precedono attorno campo esterno o campo locale
 decadono β
μ+ → e+ + ν’e + νμ
▪ emissione più intensa nella direzione di polarizzazione istantanea

informazioni su
 direzione, intensità, dinamica campo locale

vantaggi




sonda locale
selezione profondità
analisi a campo esterno nullo
senza problemi a basse T

μ spin relaxation
 detector longitudinale
prima e dopo campione
 possibiltà campo parallelo
polarizzazione
 spin μ congelato
N=N0e-t/τ(1+Acosθ)

μ spin Rotation
 campo direzione
diversa polarizzazione
 detector in direzione
trasversa
 μ impiantati precedono
N=N0e-t/τ(1+Acosωt)

μSR e grafite magnetica
 tecnica bulk
 bulk grafite magnetica non prodotto
 μ intrappolati nei difetti
 sonda selettiva

LEμSR Low Energy μ Spin Rotation
 adatta per studiare magnetismo in film sottili
 E> 5 keV no rilassamento
 E< 5 keV rilassamento

risultato uguale HOPG irraggiata e no

campo magnetico sotto gli 30nm dalla
superficie

concentrazione difetti aumenta vicino
alla superficie

μ maggiori energie per sondare
profondità e magnetismo indotto da
irraggiamento (profondità>100nm)
(Dubman, J. Mag. Mat., 2010)

riassumendo le evidenze sperimentali:
 ferromagnetismo stabile a T ambiente
▪ non dovuto alle impurezze metalliche
▪ momento magnetico aumenta con irraggiamento protoni
▪ carattere 2D
 strato magnetico superficiale
 legato elettroni π
 aumenta con struttura grafite più ordinata
 legato a:
▪ difetti
▪ bordi di grano
▪ idrogeno

perché e come???
da prima 2000:
→ previsioni teoriche
ordine magnetico grafite

 dovuto a:
▪ misto di orbitali sp2 e sp3
▪ edge zigzag
▪ bordi di grano
▪ difetti
▪ stati localizzati all’energia di fermi
▪ polarizzati mediante interazione e – e
▪ lungo range dato dall’interazione con
densità di spin del reticolo bipartito
Modello semplice per grafene: → Yazyev
One orbital mean field Hubbard model

 considera solo
▪ stati elettronici π
▪ interazioni primi vicini
▪ applica approssimazione campo medio

Hamiltoniana:
 Tight binding:
▪ modello tight-binding, primi vicini
▪ descrive bene proprietà elettroniche grafene
▪ non descrive proprietà magnetiche
(Ohldag, Phys. Rev. Let., 2007)

descrizione magnetismo
 interazione repulsiva elettrone–elettrone
 in 1 sito (corto raggio)

approssimazione campo medio:
 interazione spin-popolazione media spin sullo
stesso sito

soluzione auto-consistente del problema:
 momento magnetico locale:
 spin totale:
 dipendono entrambi da U/t

conseguenze modello:
 reticolo bipartito
 approccio matematico: benzenoid graph theory
▪ numero stati energia zero:
▪ α n° max siti non adiacenti
▪ N n° totale siti

come sono polarizzati questi stati:
 teorema di Lieb
▪ sistema bipartito
▪ modello Hubbard
▪ int. repulsiva e-e
▪ banda mezza piena
 stato fondamentale ha un momento di spin:

regole di conteggio:

studio magnetismo in frammenti di grafene
 nanoflakes, nanoislads, nanodisk

Frammenti di grafene
 esagonale
▪ NA=NB=N/2
▪ n° max siti non adiacenti
atomi appartengono ad uno dei
2 sottoreticoli α=NA
▪ η=S=0
 no magnetismo

Frammenti di grafene
 triangolare
▪ NA=12 NB=10
▪ n° max siti non adiacenti
atomi sottoreticolo dominante
α=NA
▪ η=2 stati a energia 0 nel
sublattice A
▪ S=1 stato tripletto
▪ polarizzazione toglie
degenerazione
▪ densità spin localizzata reticolo A
▪ momento magnetico indotto
▪ interazione di scambio stati pieni con
2 elettroni disaccoppiati

Frammenti di grafene
▪
▪
▪
▪
▪
NA=NB
η=2 stati a energia 0
S=0 stato singoletto
spin opposti
accoppiamento
antiferromagnetico

studio andamento Stot con dimensione
frammenti

dimensione critica oltre la quale c’è
transizione stato antiferromagnetico

Grandi layer grafene → difficile applicare
regole conteggio
 studio effetti bordo
▪ modello: strisce 1D di grafene: graphene nanoribbons
 bordi:
▪ armchair
▪ zigzag

Nanoribbons:
 modello tight_binding 1° vicini:
▪ armchair:
▪ metallici o semiconduttori
▪ dipende dallo spessore
▪ gap diminuisce con aumento spessore
▪ zigzag
▪
▪
▪
▪
metallici
andamento banda piatto
stato a E bassa localizzato sul bordo
decade velocemente nel bulk

Hubbard campo medio:
 momenti localizzati sui
bordi
 accoppiamento
▪ ferro lungo bordi
▪ antiferro tra i bordi

no prove sperimentali
magnetismo legato ai bordi

ma curve STS ai bordi zigzag
mostrano picchi di stati a
energia 0

Magnetismo nel grafene
 difetti:
▪ vacanze
▪ interstiziali
▪ chemiasorbimento idrogeno

modello 1 orbitale
 vacanza = assorbimento
H
 rimozione di un orbitale
pz
 effetti sulla struttura
elettronica
 creazione supercelle

si forma uno stato a E=0
e un momento sul reticolo
complementare
 decadimento legge a potenza
 DOS calcolata per vacanze e
assorbimento H
▪ H: stati localizzati
▪ Vacanza: stati localizzati + stati
complementari dovuti ai legami
rotti

distribuzione random
difetti
 Teorema Lieb:
 accoppiamento
▪ ferro sullo stesso sottoreticolo
▪ antiferro tra i 2 sotto-reticoli

Magnetismo nella grafite
 aumenta con irraggiamento

cause?
 difetti nei piani di grafene
 impacchettamento piani


sottoreticoli popolati differentemente dai difetti
ordine ferrimagnetico

ordine magnetico HOPG
confermato
 ma ancora segnali deboli

spiegazioni teoriche:
 ipotesi e calcoli teorici
▪ difetti

ancora molto lavoro da fare
 per una teoria verificata e
complessiva
▪ nuova teoria magnetismo?
Takahashi et al 1991 Phys. Rev. Lett. 67 746
Makarova et al 2001 Nature 413 716
 Esquinazi et al 2002 Phys. Rev. B 66, 024429
 Esquinazi et al. 2003 Phys. Rev. Lett. 91 227201
 Cervenka et al. 2009 NaturePhys. 5 840–4
Kopelevich et al. 2000 J. Low Temp. Phys 119 691
 Barzola-Quiquia et al. 2007 Phys. Rev. B 76 161403
 Hohne, Esquinazi 2002 Adv. Matter 14 753
 Ohldag et al. 2007 Phys. Rev. Lett. 98 187204
Palacio, 2001 Nature 413 690
 Yazyev O. et al. 2007 Phys. Rev. B 75 125408
 Yazyev O. V 2008 Phys. Rev. Lett. 101 037203
 Yazyev O. Rep.2009 Prog. Phys. 73 056501
Dubman et al. 2010 J.Mag. Mag. Mat. 322 1228–1231
Final Report “Ferrocarbon” Project 2008
Makarova, “Magnetism Of Carbon-based Materials”, Review, 2002
