Master di II° livello in Didattica delle Scienze
Corsista: Paola Favaron
Erica Strani
Report:
Il magnetismo
Quando un magnete viene avvicinato ad altri oggetti determina in alcuni di essi dei
comportamenti evidenti: spostamento, rotazione e attacco, che fanno ipotizzare che nello
spazio circostante qualcosa sia cambiato e supporre la possibile presenza di “sottili fili invisibili”
che fanno muovere a attirano a sé alcuni tipi di oggetti.
Per incominciare a indagare lo spazio attorno ad un magnete, si è fatto uso di un materiale
sensibile alla presenza del magnete.
LO SPAZIO INTORNO AI MAGNETI
Nodo concettuale: visualizzare il campo magnetico di un magnete.
Obiettivo generale: visualizzare l’esistenza delle linee di campo utilizzando materiale
ferromagnetico.
Obiettivo specifico: verificare che lo spazio circostante un magnete acquista la proprietà di
orientare aghi di acciaio ferromagnetici.
Materiale:
Lana d’acciaio tagliata finemente;
Lastra di vetro;
Magnete ricurvo.
Modalità operativa: si taglia finemente la lana d’acciaio, si appoggia la lastra di vetro sopra i
poli del magnete e vi si sparge sopra la lana d’acciaio.
Ipotesi: la lana d’acciaio dovrebbe disporsi lungo le linee del campo magnetico, rendendo di
converso evidente l’andamento del campo stesso.
Nella foto si vede chiaramente la
disposizione dei pezzetti d’acciaio.
Osservazione: per quest’esperienza di fatto si evidenziano bene le linee del campo sul piano
dato dalla lastra di vetro, tuttavia si può supporre che la proprietà del campo si estenda allo
spazio intorno, come si può dedurre dalla foto successiva dove si vede che la lana d’acciaio si
accumula su se stessa.
1
L’AGO DELLA BUSSOLA SI DISPONE LUNGO LE LINEE DEL CAMPO
Nodo concettuale: Visualizzare le linee del campo
Obiettivo generale: “Mappare” lo spazio attorno ad un magnete, utilizzando le interazioni
bussola – magnete.
Obiettivo specifico: Utilizzare una bussola per evidenziare le linee del campo del magnete;
Materiali:
Una bussola;
1 magnete a barra;
Foglio di carta;
Matita.
Metodo:
Posizionare il magnete sul foglio e tenerlo fermo. Avvicinare la bussola e con la
matita segnare le posizioni delle punte dell’ago. Spostare la bussola in modo che i
punti formino delle sequenze continue. Ripetere le operazioni allontanandosi un po’
alla volta dal magnete quindi congiungere i punti ordinatamente.
Ipotesi: Le posizioni che assume l’ago della bussola indicano che lo spazio attorno al magnete
ha delle proprietà che si esplicano attraverso delle linee particolari.
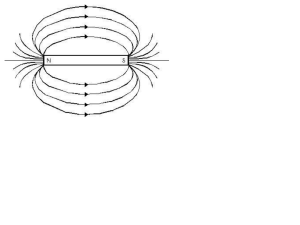
Conclusione: La bussola ha permesso di evidenziare delle linee che escono da un polo ed
entrano nell’altro. Questo comportamento è reso evidente dalla rotazione dell’ago e permette
di ipotizzare che le linee uscenti quasi verticalmente dai poli appartengano a linee di campo via
via più grandi e che anche all’interno del magnete esistano queste linee.
2
INTERAZIONI TRA DUE MAGNETI: UNO VINCOLATO L’ALTRO LIBERO
Nodo concettuale: l’interazione tra due magneti
Obiettivo generale: riconoscere che due magneti interagiscono l’uno con l’altro
Obiettivo specifico: individuare i comportamenti di un magnete libero di muoversi rispetto ad
uno fisso.
Materiali:
Un magnete appeso ad un filo;
Un magnete libero.
Metodo:
Osservazione
Modalità operativa:
Avvicinare il magnete libero a quello sospeso e osservare;
Ipotesi: il magnete libero tende a ruotare in modo da posizionarsi con il polo opposto rispetto
all’altro, tra i due si esercita così una forza attrattiva.
Osservazioni: se vengono avvicinati i poli opposti dei
due magneti, tra quello libero di muoversi e l’altro si
esercita una F attrattiva.
Quando vengono avvicinati poli dello stesso tipo, il
magnete appeso assume la posizione più lontana,
spinto dalla forza repulsiva. Quando si avvicina
ulteriormente
il
magnete
libero
all’altro,
quest’ultimo compie una rotazione opponendo il
polo opposto e si attacca all’altro.
Conclusioni: il comportamento osservato conferma l’ipotesi iniziale.
3
PORTATA DI UN MAGNETE
Obiettivo generale: Studiare le caratteristiche delle interazioni magnetiche.
Obiettivo specifico: Riconoscere l’importanza delle condizioni di interazione;
Misurare la portata di un magnete.
Materiali:
Due magneti;
Alcune biglie d’acciaio (abbiamo a disposizione solo 8 biglie);
Metodo:
Tenendo in mano un magnete, avvicinarlo alle biglie per farle attaccare
una dopo l’altra. Ripetere più volte l’operazione per assicurarsi che il magnete agisca
affettivamente sempre nello stesso modo.
La Forza Peso rappresentata dal numero di biglie è
equilibrata dalla Forza Attrattiva del magnete.
Un singolo magnete è in grado di attrarre 5 biglie.
Proviamo a unire per i poli opposti due magneti uguali e
ripetiamo
l’esperimento:
Il risultato non è cambiato, quindi possiamo affermare che la forza attrattiva di due magneti in
serie è la stessa del magnete singolo.
Proviamo ora ad unire i due magneti, accostandoli per gli stessi poli e vediamo quante biglie
vengono attratte.
Tutte le 8 biglie sono state attratte.
Due magneti in parallelo manifestano una forza attrattiva
molto superiore a quelli in serie.
CONCLUSIONI:
Possiamo misurare la forza peso che viene equilibrata da quella attrattiva di un magnete, cioè
la sua portata. Possiamo affermare che condizioni diverse di interazione producono risultati
diversi. Non possiamo affermare che vi sia una proporzionalità diretta fra posizione reciproca
dei magneti e la loro portata, in quanto non disponevamo di biglie sufficienti (10) per
verificarlo.
4
DISTANZA TRA MAGNETI
Nodo concettuale: le interazioni magnetiche sono in funzione della distanza
DEVIAZIONE DELL’AGO DI UNA BUSSOLA IN PROSSIMITÀ DI UN CAMPO MAGNETICO
SUPPLEMENTARE A QUELLO TERRESTRE
Obiettivo generale: riconoscere che l’ago di una bussola, disposto lungo la direzione del campo
magnetico terrestre, subisce una deviazione quando la bussola viene
avvicinata ad un magnete.
Obiettivo specifico: determinare, misurando gli spostamenti dell’ago della bussola dalla
posizione iniziale, come le interazioni magnetiche dipendano dalla distanza.
Materiali:
Un foglio di carta centimetrata;
un magnete;
una bussola;
Modalità d’esecuzione:
si ricerca una zona lontana da materiali ferromagnetici, in modo da evitare
il formarsi di campi magnetici aggiuntivi a quello del magnete utilizzato;
si traccia lungo un lato del foglio una linea, che dovrà coincidere con la
direzione dell’ago della bussola, inizialmente lungo la direzione N-S;
centralmente e perpendicolarmente ad essa, si traccia un’altra linea alla cui
estremità verrà posizionato il magnete;
lungo la linea centrale si tracciano delle tacche a intervalli regolari, dove
viene via via posizionata la bussola avvicinandola al magnete;
si sposta la bussola e si segnano le diverse posizione assunte dal suo ago.
Dell’esperienza si sono prodotte tre versioni.
Prima esperienza
In questo caso si sono usati intervalli di 8 cm a cominciare da una distanza di 80 cm; a
distanza > 80 l’influenza del campo magnetico del geomag è così debole da non consentire
rilevazioni apprezzabili, da 72 cm si osserva la prima deviazione dell’ago.
Il vettore B (vettore di campo magnetico) alla posizione iniziale della bussola è dato
dalla posizione N-S dell’ago della bussola, ovvero come segmento normale (lunghezza 1 cm)
5
alla direzione della linea di spostamento della bussola; per le misurazioni successive si è
segnata la posizione dell’ago della bussola e misurata la sua proiezione sulla retta graduata
(degli spostamenti), ovvero si è considerato il senα dove α è l’angolo formato dal vettore B
rispetto alla posizione iniziale sotto l’influenza del campo magnetico prodotto dal magnete.
Nella posizione di partenza, la bussola risente solamente del campo magnetico terrestre
e la direzione indicata dal suo ago non risente della vicinanza del magnete.
Quando si avvicina la bussola al magnete, lungo la retta perpendicolare, si osserva lo
spostamento dell’ago; la nuova direzione è la risultante dell’azione del campo magnetico
terrestre e del magnete e, dal momento che l’azione del campo terrestre non varia, è plausibile
affermare che il cambiamento sia attribuibile all’influenza del magnete.
Si osserva che, avvicinando la bussola al magnete, l’ago della bussola dalla direzione NS si sposta verso E- O. Si nota, leggendo i dati in tabella, che le deviazioni di B, date dalle
proiezioni Bx su Bi, inizialmente sono minime, ma aumentano poi considerevolmente, fino a
raggiungere un valore prossimo all’∞ che qui non è stato riportato.
B
0,2
0,3
0,46
0,64
0,9
1,4
2,5
5,62
distanza in cm
72
64
56
48
40
32
24
16
Secondo le ipotesi, l’influenza del campo magnetico dovrebbe essere inizialmente quella
propria di un polo magnetico poi, avvicinando la bussola al geomag, si esplicherebbe come
propria di un dipolo magnetico, sicché la variazione di B nelle prime misurazioni dovrebbe
crescere con il quadrato della distanza magnete-bussola e poi, nelle successive misurazioni,
crescere con il cubo della medesima distanza. Secondo l’ipotesi B·d2 e poi B·d3 dovrebbero dare
una relazione lineare per gli intervalli considerati.
B*d*d
B*d*d*d
1036,8 74649,6
1228,8 78643,2
1442,56 80783,36
1474,56 70778,88
1440
57600
1433,6 45875,2
1440
34560
1438,72 23019,52
Dalla tabella e dai grafici si evince che per le prime misure il coefficiente di
regressione lineare della relazione quadratica è 0,93 (quasi cioè prossimo a 1), mentre per
le seconde misure, secondo la relazione cubica, è addirittura =1.
Se invece si prende in considerazione il grafico di tutti i valori B*d2, si nota che mentre
nel caso della relazione cubica è addirittura 1.
6
d*d
distanze 72-64-56-48
1800
1600
1400
1200
1000
800
600
400
200
0
R2 = 0,9323
Serie1
Lineare (Serie1)
0
1
2
3
4
5
B
distanze 40-32-24-16
d*d*d
R2 = 1
70000
60000
50000
40000
30000
20000
10000
0
Serie1
Lineare (Serie1)
0
1
2
3
4
5
B
Se invece prendiamo in considerazione R ottenuto su tutti i valori ricavati dalla relazione
Bm·d2, si nota che esso scende a 0,5211,
1800
2
R = 0,5211
1600
1400
1200
1000
800
600
400
Serie1
200
Lineare (Serie1)
0
0
2
4
6
8
10
mentre il coefficiente di correlazione del grafico di tutti i valori B*d 3 scende a 0, 88.
7
100000
R2 = 0,8817
90000
80000
70000
60000
Serie1
Lineare (Serie1)
50000
40000
30000
20000
10000
0
0
2
4
6
8
10
In ogni caso è un valore più alto del precedente, tale che parrebbe la natura di dipolo
magnetico propria del magnete considerato, sia prioritaria rispetto all’influenza dell’unico polo
più prossimo alla bussola, il che potrebbe trovare una spiegazione nel magnete usato, non
troppo lungo, tale cioè che distanza tra i due poli N-S non sia rilevante rispetto alla forza
magnetica esercitabile dai due poli considerati singolarmente.
Seconda esperienza
Eseguita per avvalorare la tesi riscontrata nel primo esperimento.
Si riporta come sopra la tabella dei dati registrati e dei calcoli effettuati.
Bm (cm)
d (cm)
non registrabile
0,2
0,4
0,7
2,6
5,3
15
Bm*d*d
24
21
18
15
12
9
6
Bm*d*d*d
88,2
129,6
157,5
374,4
429,3
540
1852,3
2332,8
2362,5
4492,8
3863,7
3240
Si analizzano prima i grafici riferiti all’intera serie di dati e poi solo quelli relativi agli
intervalli evidenziati dai colori:
8
d2·Bm
2
R = 0,7493
700
600
500
400
d*d
300
200
100
0
0
2
4
6
8
10
12
14
16
14
16
Bm
Bmd^3
R2 = 0,1311
5000
4500
4000
3500
d*d*d
3000
2500
2000
1500
1000
500
0
0
2
4
6
8
Bm
9
10
12
Come si osserva i valori di R2 sono bassi in entrambi i casi, specie nel caso della
relazione cubica.
Si prova quindi a spezzare i dati in due serie e a farne il relativo diagramma.
distanza 21-18-15
2
R = 0,9494
180
160
140
120
d*d
100
80
60
40
20
0
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
14
16
Bm
distanza 12 - 9-6
R2 = 0,9025
5000
4500
4000
3500
d*d*d
3000
2500
2000
1500
1000
500
0
0
2
4
6
8
10
12
Bm
Si trova che per le prime tre misure R2 è 0,9872, mentre per le successive è addirittura
uguale a 1, ciò che pare confermare le osservazioni esposte sopra.
10
Terza esperienza
La modalità operativa è quella descritta in precedenza, ma si prova a variare la
regolarità degli intervalli di posizionamento della bussola per vedere se cambia qualcosa.
Nella tabella sono riportate la varie distanze ed i valori di Bm, inoltre in foto si riporta il
grafico di rilevamento delle misure di Bm.
Distanza (cm)
26
24,7
22
19,5
17
15
13
10
Bm
1,2
1,5
1,7
1,9
2,5
3,3
7,8
9,0
Il grafico relativo ai dati rilevati è il seguente:
Deviazione dell'ago della bussola
2
R = 0,7666
10
9
8
7
6
5
4
3
2
1
0
30
27
24
21
18
15
distanza
11
12
9
6
3
0
Bm
distanza
Bm
(cm)
(cm)
26
1,2
24,7
1,5
22
1,7
19,5
1,9
17
2,5
15
3,3
13
7,8
10
9
Nel grafico la linea di tendenza e R2 (coefficiente di regressione che indica quanto è
buona l’approssimazione che avvicina la curva alla retta) indicano che non si tratta di una
relazione lineare.
Come sopra si calcola il quadrato della distanza per il vettore Bm (d 2 ·Bm) e si guarda
all’andamento dei valori.
2
d
676
610,09
484
380,25
289
225
169
100
R2 = 0,671
Bm (cm)
1,2
1,5
1,7
1,9
2,5
3,3
7,8
9
D · Bm
811,2
915,135
822,8
722,475
722,5
742,5
1318,2
900
2
Deviazione dell'ago della bussola
10
9
8
7
6
5
4
3
2
1
800
700
600
500
400
300
200
100
0
0 -1
Anche in questo caso il coefficiente di regressione lineare è basso (0,671); visti gli
esperimenti precedenti, dove si era evidenziata una prima relazione quadratica tra le misure
rilevate ed una cubica per i valori segnati all’avvicinare la bussola al magnete, si prova a
vedere se anche in questo caso non ci sia un analogo andamento dei valori. In effetti, dalle
tabelle dei dati si vede che le prime misurazioni rispondono più regolarmente ad una relazione
di tipo quadratico, mentre le successive ad una relazione di tipo cubico.
particolare relativo alle distanze al quadrato: 19,5 - 17
- 15
380,25
1,9
722,475
289
2,5
722,5
225
3,3
742,5
12
distanze: 19,5 - 17 -15
3,5
3
2,5
2
R = 0,9668
2
1,5
1
0,5
0
400
350
300
250
200
150
100
50
0
Si nota che R2 sale a 0,9668.
Elevando al cubo la distanza e calcolando il prodotto d3 ·Bm si ottiene:
3
d
17576
15069,223
10648
7414,875
4913
3375
2197
1000
Bm (cm) d · Bm
1,2
21091,2
1,5
22603,83
1,7
18101,6
1,9
14088,26
2,5
12282,5
3,3
11137,5
7,8
17136,6
9
9000
3
e rappresentando graficamente i dati evidenziati in giallo si ricava un valore di R2=0,9272.
particolare distanza al cubo: 26 - 24,7 - 22
17575
15069,223
10648
d^3 (26- 24,7 - 22)
1,2
1,5
1,7
R2 = 0,9272
2
1,8
1,6
1,4
1,2
1
0,8
0,6
0,4
0,2
0
20000
15000
10000
5000
13
0
Si verificano degli andamenti dei valori quasi lineari, secondo le leggi evidenziate nei
due precedenti esperimenti.
Conclusione
Si conferma il medesimo comportamento dell’ago della bussola, il quale viene deviato
dalla propria direzione N-S (direzione del campo magnetico terrestre), sotto l’azione di un
magnete che eserciti un campo magnetico supplementare. Eventuali variazioni nello
spostamento dell’ago della bussola si potrebbero supporre in rapporto al tipo di magnete
impiegato.
MISURA DELLA VARIAZIONE DELLA FORZA MAGNETICA REPULSIVA TRA DUE MAGNETI, IN
INTERAZIONE CON UNA FORZA PESO VARIABILE CRESCENTE IN MODO DISCRETO
Si sono effettuati due esperimenti.
Nel secondo caso ci si è attenuti a verificare la legge di correlazione tra la forza e la
distanza come inversamente quadratica, cubica e alla quarta potenza.
Nel primo esperimento si è provato anche a scorporare i dati, come per l’esperienza
sulla deviazione dell’ago di una bussola, con l’intenzione di verificare se avvicinandosi i
magneti una delle tre leggi fosse più congruente delle altre. Si è voluto porre un problema,
consapevoli che occorrerebbero ben altre prove empiriche a sostegno di un’eventuale tesi di
questo tipo.
Nodo concettuale: la forze repulsiva fra poli magnetici uguali e vincolati è in relazione alla
distanza tra gli stessi.
Obiettivo generale: riconoscere che l’azione esercitata da dei pesetti interagisce con la forza
repulsiva tra i magneti.
Obiettivo specifico: individuare se esiste una relazione fra la variazione della forza peso (Fp)
esercitata dai pesetti e la forza repulsiva magnetica agente tra i magneti.
Materiali:
due geomag, un tubo in plexiglas chiuso ad un estremo da un tappo di
plastica;
7 pezzi di materiale non ferromagnetico, tali cioè da valere solo come
produttori di campo gravitazionale e non anche magnetico.
Modalità di esecuzione:
si posizionano dentro il tubo i due geomag, di modo che si affaccino
ciascuno verso l’altro con il medesimo polo, si rileva su una scala graduata
millimetrata lungo il tubo la distanza tra i due magneti;
si inizia a mettere i 7 pesetti, uno a uno effettuando di volta in volta la
misura della distanza tra i due geomag.
Ipotesi:
la forza gravitazionale esercitata dai pesi dovrebbe agire su quella repulsiva
magnetica, avvicinando mano a mano i due geomag, all’aumentare della
Fp.
In questo caso si sono effettuati due esperimenti.
Prima esperienza
Dalle misure effettuate si rileva e si osserva che
c’è avvicinamento tra i due geomag
14
Si sa che la forza magnetica aumenta secondo l’inverso del quadrato, come d’altronde la
gravitazionale, ci si chiede se la Fm segua la medesima legge o se non vi sia interazione tra le
due.
Dai dati rilevati e dai grafici relativi si nota che
peso
1
2
3
4
5
6
7
d in mm
17
14
12,5
11,5
11
10
9,5
all’aumentare del numero di pesi diminuisce la distanza tra i due geomag; si procede
quindi a verificare matematicamente se il variare dei valori risponda meglio ad una legge
inversamente quadratica o cubica o addirittura alla quarta potenza.
p*100/d*d
p*1000/d*d*d p*10000/d*d*d*d
0,35
0,20
0,12
1,02
0,73
0,52
1,92
1,54
1,23
3,02
2,63
2,29
4,13
3,76
3,42
6,00
6,00
6,00
7,76
8,16
8,59
Dai grafici completi dei valori si evince che tra le tre relazioni, la relazione inversamente
quadratica è quella che nell’insieme dei valori presenta un coefficiente di regressione più vicino
a 1.
1/d*d
interazione
9,00
8,00
7,00
6,00
5,00
4,00
3,00
2,00
1,00
0,00
-1,00 0
2
R = 0,9701
Serie1
Lineare (Serie1)
2
4
6
8
p
15
interazione
10,00
1/d*d*d
8,00
R2 = 0,9419
6,00
Serie1
4,00
Lineare (Serie1)
2,00
0,00
-2,00 0
2
4
6
8
p
interazione
10,00
1/d*d*d*d
8,00
2
R = 0,9103
6,00
Serie1
4,00
Lineare (Serie1)
2,00
0,00
-2,00
0
2
4
6
8
P
Tuttavia, esaminando più nel particolare la curva dei valori, si trova che
intervallo 1-4
3,50
3,00
R2 = 0,9885
1/d*d
2,50
2,00
Serie1
1,50
Lineare (Serie1)
1,00
0,50
0,00
0
1
2
3
4
5
p
16
1/d*d*d
intervallo 5-7
9,00
8,00
7,00
6,00
5,00
4,00
3,00
2,00
1,00
0,00
2
R = 0,9999
Serie1
Lineare (Serie1)
0
1
2
3
4
B
intervallo 5-7
10,00
R2 = 1
1/d*d*d*d
8,00
6,00
Serie1
4,00
Lineare (Serie1)
2,00
0,00
0
1
2
3
4
p
il coefficiente della relazione quadratica considerato solo per le prime quattro misure
diventa 0,988 invece che 0,970, mentre per le successive 3 misure il coefficiente della
relazione cubica da 0,942 sale a 0,999 e quello della relazione alla quarta potenza addirittura
cresce da 0,930 a 1.
Si sono considerati gli intervalli 1-4 e 5-7, in quanto dalla tabella di misura delle
distanze rilevate si nota che l’avvicinamento tra i due magneti nelle ultime tre misure procede
per intervalli più piccoli che non nelle prime 4 misurazioni.
Parrebbe che, avvicinandosi i magneti, la forza repulsiva tra gli stessi divenisse più
intensa tale che anche la forza peso a contrasto debba essere maggiore. Inoltre, quando i due
magneti si avvicinano sotto l’effetto dell’aumento della Fp, si può supporre che la forza
magnetica repulsiva tra i due geomag non sia solo quella dei due poli interessati, ma sia
dovuta più propriamente alla caratteristica dipolare dei due magneti stessi. Perciò la risultante
dell’azione delle forze in gioco potrebbe essere tale da venir meglio interpretata con una legge
inversamente cubica, se non addirittura alla quarta potenza.
Nell’esperimento effettuato si segnala la difficoltà di ottenere delle misure ripetibili, dal
momento che i pesi non sono tutti eguali, cosicché cambiando il loro ordine di entrata si
avvertono della variazioni di misura di circa 1-2 mm, il che non è poco date le distanze in
esame; occorrerebbe dunque numerare i pesi di modo che i diversi misuratori, di volta in volta,
abbiano una stessa sequenza di misure. Si ridurrebbe così almeno la possibilità degli errori, per
quanto concerne l’aspetto della riproducibilità di una misura.
17
Seconda esperienza
Materiali:
2 magneti;
un tubicino in vetro;
12 pesetti in vetro.
Modalità operativa: si è operato come nel caso precedente, ricavando la seguente tabella dati:
n° pesi
0
1
2
3
4
5
6
d
(mm)
22,5
21
19
18
17
16,5
16
1/d^2
1/d^3
1/d^4
0,001975309
8,77915E-05
3,90184E-06
0,002267574
0,00010798
5,14189E-06
0,002770083
0,000145794
7,67336E-06
0,00308642
0,000171468
9,52599E-06
0,003460208
0,000203542
1,1973E-05
0,003673095
0,000222612
1,34916E-05
0,00390625
0,000244141
1,52588E-05
da cui, come nel caso precedente si ricavano i tre grafici complessivi
18
forza di repulsione e d^2
2
R = 0,9856
0,0045
0,004
0,0035
0,003
1/d^2
0,0025
0,002
0,0015
0,001
0,0005
0
0
1
2
3
4
5
6
7
n° pesi
forza di repulsione e d^3
R2 = 0,9922
0,0003
0,00025
1/d*d*d
0,0002
0,00015
0,0001
0,00005
0
0
1
2
3
4
n° pesi
19
5
6
7
forza di repulsione e d^4
2
R = 0,995
0,000018
0,000016
0,000014
0,000012
1/d^4
0,00001
0,000008
0,000006
0,000004
0,000002
0
0
1
2
3
4
5
6
7
n° pesi
I risultati ottenuti non richiedono ulteriori elaborazioni, come nelle esperienze precedenti, in
quanto il valore di R via via crescente dimostra che la forza di tipo repulsivo necessaria ed
equilibrare la forza peso esercitata sul magnete è inversamente proporzionale alla quarta
potenza della distanza. In questo seconda esperienza, è ipotizzabile che i pesetti di vetro e il
materiale usato abbiano consentito misurazioni più attendibili.
20