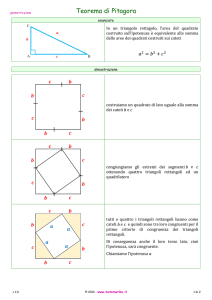
I TRIANGOLI RETTANGOLI
IN QUESTA ATTIVITÀ PARLEREMO DI TRIANGOLI RETTANGOLI, PERTANTO RICORDA CHE I LATI DI TALI TRIANGOLI HANNO NOMI
PARTICOLARI:
SI CHIAMANO CATETI DI UN TRIANGOLO RETTANGOLO ABC I DUE LATI AB E
AC CHE SONO TRA LORO PERPENDICOLARI
(FORMANO UN ANGOLO DI 90°)
IL TERZO LATO BC, OPPOSTO ALL’ANGOLO RETTO, SI CHIAMA IPOTENUSA.
RIPASSA IN ROSSO I CATETI E IN VERDE L’IPOTENUSA DEI TRIANGOLI RETTANGOLI DELLA FIGURA
SEGUENTE.
LA LEGENDA
SECONDO
DEL TEOREMA
LA LEGGENDA
PITAGORA
SCOPRÌ IL SUO TEOREMA MENTRE ERA IN ATTESA DI ESSERE RICEVUTO DAL
TIRANNO DELLA CITTÀ GRECA DI SAMO.
IL PAVIMENTO DELLA
SALA DI RICEVIMENTO SI PRESENTAVA PIASTRELLATO COME IN FIGURA, DOVE IN GIALLO È
EVIDENZIATO QUANTO
PITAGORA OSSERVÒ, A PARTIRE DAL TRIANGOLO OTTENUTO DIVIDENDO UNA PIASTRELLA
LUNGO LA SUA DIAGONALE.
SCRIVI COSA OSSERVI RELATIVAMENTE AI QUADRATI COSTRUITI SUI CATETI
.............................................................................................................
.............................................................................................................
.............................................................................................................
.............................................................................................................
LA DIMOSTRAZIONE DI PERIGAL
TRA
LE TANTE DIMOSTRAZIONI DEL TEOREMA DI
PITAGORA,
VI PROPONGO
PERIGAL CON LA PASSIONE PER LA MATEMATICA.
PROVIAMOCI ANCHE NOI.
RITAGLIA I QUADRILATERI A, B, C, D, E
INCOLLA IL TRIANGOLO E IL QUADRATO GRANDE SUL QUADERNO
RIEMPI IL QUADRATO GRANDE CON I 5 QUADRILATERI
QUELLA DELL'AGENTE DI CAMBIO
HENRY
IN PRATICA, SI DIMOSTRA CHE:
Q1
+
=
Q2
QUINDI LA SOMMA DI Q1 + Q2 È EQUIVALENTE A
Q3
Q3
OVVERO:
LA SOMMA DELLE AREE DEI QUADRATI Q1 E
Q2 È EQUIVALENTE ALL’AREA DEL QUADRATO Q3
FORMALIZZIAMO:
Q1 + Q2 = Q3
OSSERVIAMO LA FIGURA INIZIALE
Q1
Q3
C1
i
C2
Q2
CI RENDIAMO CONTO CHE:
AB = C2 =CATETO MAGGIORE DEL TRIANGOLO = LATO DEL QUADRATO Q1
AC= C1= CATETO MINORE DEL TRIANGOLO = LATO DEL QUADRATO Q2
BC= i =
IPOTENUSA DEL TRIANGOLO = LATO DEL QUADRATO
Q3
QUINDI:
Q1= QUADRATO COSTRUITO SUL CATETO MAGGIORE
Q2= QUADRATO COSTRUITO SUL CATETO MINORE
Q3= QUADRATO COSTRUITO SULL’IPOTENUSA
A QUESTO PUNTO HAI TUTTI GLI ELEMENTI PER SCRIVERE L’ENUNCIATO DEL TEOREMA DI PITAGORA:
.............................................................................................................
.............................................................................................................
.............................................................................................................
.............................................................................................................
APPLICAZIONE DEL TEOREMA DI PITAGORA
i
C2
C1
POICHE’
Q1= QUADRATO COSTRUITO SUL CATETO MAGGIORE
Q2= QUADRATO COSTRUITO SUL CATETO MINORE
C1
C2
Q3= QUADRATO COSTRUITO SULL’IPOTENUSA i
SAPENDO CHE L’AREA DEL QUADRATO E UGUALE A:
A= l2
POSSIAMO AFFERMARE CHE:
Q1= C12
Q2= C22
Q3= i2
RICORDANDO CHE:
Q1 + Q2 = Q3
POSSIAMO SCRIVERE:
i2 = C12 + C22
ABBIAMO TROVATO UNA FORMULA CHE CI PERMETTE DI TROVARE L’IPOTENUSA, CONOISCENDO I
CATETI.
GRAZIE ALLE FORMULE INVERSE È POSSIBILE TROVARE UN CATETO.
C12= i2 - C22
C22 = i2 - C12
ESEMPIO 1
C1 = 6 cm
C2 = 8 cm
i=?
i 2 = C1 2 + C2 2
i2 = 62+82
i2 = 36 + 64 = 100
ATTRAVERSO QUESTO CALCOLO TROVO L’IPOTENUSA AL QUADRATO;
COME FARE PER TROVARE LA SOLUZIONE?
SE
ALLORA
i2 = 100
i = 100 = 10
cm
ESEMPIO 2
i = 15 cm
C1 = 12 cm
C2 = ?
C22 = i2 - C12
C22 = 152 - 122
C22 = 225 -144 = 81
ANCHE IN QUESTO CASO:
SE C22 = 81
ALLORA C2=
81 9
cm
PER PROVARE SE HAI CAPITO ESEGUI I SEGUENTI ESERCIZI
1. Calcolo della misura della diagonale di un rettangolo.
DISEGNA UN RETTANGOLO ABCD
TRACCIA LA DIAGONALE AC.
a. CHE TIPO DI TRIANGOLI SONO ABC E CDA? ..................................
b. COME SONO FRA LORO QUESTI TRIANGOLI? ..................................
c. CALCOLA LA MISURA DELLA DIAGONALE AC DI UN RETTANGOLO CON I LATI DI 40 CM E 30 CM.
AC 2 = ....
AC = .....
2. Calcolo della misura dell’altezza di un triangolo isoscele.
DISEGNA UN TRIANGOLO ISOSCELE ABC.
TRACCIA L’ALTEZZA
CH RELATIVA AL LATO AB.
a. CHE TIPO DI TRIANGOLI SONO ACH E BCH? ..................................
b. COME SONO FRA LORO QUESTI TRIANGOLI? ..................................
c. CALCOLA LA MISURA DELL’ALTEZZA RELATIVA ALLA BASE DI UN TRIANGOLO ISOSCELE SAPENDO CHE LA BASE
MISURA
2
CH
80 CM E CIASCUNO DEI LATI CONGRUENTI È 58 CM.
=
CH =
3. Applicazioni del Teorema di pitagora ai rettangoli
ABCD E EFGH SONO RETTANGOLI.
SAPENDO CHE:
-
AD = AE = 8 CM
-
EB = 5 CM
-
IL TRIANGOLO EBF E IL TRIANGOLO FCG SONO
RETTANGOLI ISOSCELI
CALCOLA IL PERIMETRO E L'AREA DEL RETTANGOLO EFGH.
4. Applicazioni del Teorema di pitagora in situazioni reali
4.1. QUANTO DOVRÀ ESSERE LUNGO IL CAVO DI ACCIAIO CHE TRATTIENE
L’ANTENNA TELEVISIVA?
4.2. QUANTO È ALTA LA PARETE CENTRALE DEL SOLAIO?
4.3. QUANTO È LUNGO IL CORRIMANO?
4.4. A CHE ALTEZZA POGGERÀ SULLA PARETE DELLA CASA UNA SCALA
LUNGA
15 M, SE IL PIEDE È A 5 M DALLA PARETE?
4.5. DI QUANTI CENTIMETRI FUORIESCE UNA CANNUCCIA LUNGA 20 CM DAL
FORO DI UNA LATTINA CILINDRICA DI ALTEZZA 11 CM CON IL DIAMETRO DI
BASE DI 6 CM, SE LA SI IMMERGE IL PIÙ POSSIBILE SENZA PIEGARLA?
4.6.
LA MISURA DEL LATO DI OGNI QUADRATO DELLA GRIGLIA È DI 2 CM,
CALCOLA L’AREA E IL PERIMETRO DEL POLIGONO A
4.7.
4.8.
UNA SCALA A PIOLI LUNGA 3 M È APPOGGIATA AL MURO
LA BASE DISTA DAL MURO 1M.
A QUALE ALTEZZA DAL SUOLO È APPOGGIATA L’ALTRA ESTREMITÀ DELLA
SCALA?
IN UNA TAVOLETTA BABILOMESE DEL 1800 A.C. SI LEGGE IL SEGUENTE QUESITO:
“UN BASTONE LUNGO 10 UNITÀ È APPOGGIATO AD UN MURO (FIGURA A). POI SCIVOLA DI 2 UNITÀ (FIGURA B).
DI QUANTE UNITÀ IL PIEDE DEL BASTONE SI È ALLONTANATO DALLA BASE DEL MURO?”
□ A. 6 UNITÀ
□ B. 8 UNITÀ
□ C. 10 UNITÀ
□ D.12 UNITÀ
4.9.
NEL DISEGNO VEDI UN CAMPO DA CALCETTO DI FORMA
RETTANGOLARE, ROBERTO E CARLO SI SFIDANO A UNA GARA DI
CORSA: PARTENDO DALL’ANGOLO INDICATO CON
A DEVONO
ARRIVARE ALL’ANGOLO B.
ROBERTO CORRE LUNGO IL BORDO DEL CAMPO, INVECE CARLO
CORRE LUNGO LA DIAGONALE DEL CAMPO
a.
QUANTI METRI IN PIÙ DEVE PERCORRERE ROBERTO?
□ A. 50
□ B. 70
□ C. 20
□ D. 30
b. SCRIVI IL PROCEDIMENTO CHE HAI SEGUITO
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
4.10.
IL SIGNOR GIOVANNI SCENDE DAL TRAM ALL’INCROCIO DI VIA PIETRO MICCA CON VIA ANTONIO GIUSEPPE
BERTOLA
(NELLA MAPPA CHE VEDI UQI SOTTO IL PUNTO È CONTRASSEGNATO DA UN ASTERISCO)
200 METRI DI VIA
PERCORRE
BERTOLA E ALL’INCROCIO CON VIA
20 SETTEMBRE SVOLTA A SINISTRA;
DOPO AVER CAMMINATO PER 150 METRI, RAGGIUNGE L’INCROCIO CON VIA PIETRO MICCA.
DA LÌ DECIDE DI TORNARE AL PUNTO DI PARTENZA LUNGO LA VIA PIETRO MICCA.
QUANTI METRI ALL’INCIRCA PERCORRE AL RITORNO?
□ A. 200 M
□ B. 250 M
□ C. 350 M
□ D. 600 M