Studio di una funzione razionale fratta

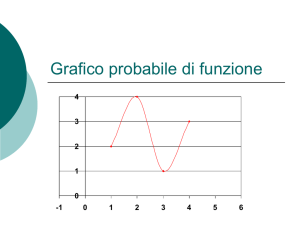
Studio di una funzione razionale fratta
Nella figura è rappresentata la funzione
1. Quale tra gli insiemi proposti è il suo CDE?
a)
b)
c)
d) nessuno dei precedenti
2. La funzione presenta un asintoto verticale di equazione ...
a)
b) x = 0
c)
x=1
d) nessuno dei precedenti
3. La funzione ...
a) interseca l'asse x nel punto (-1/2,0)
b) interseca l'asse x nel punto (1/2,0)
c)
interseca l'asse x nel punto (0,0)
d) non interseca l'asse x
4. In quale tra gli insiemi proposti, la funzione risulta positiva?
a)
b)
c)
d) nessuno dei precedenti
Nella figura è rappresentata la funzione
1. Quale tra gli insiemi proposti è il suo Dominio?
a)
b)
c)
d)
nessuno dei precedenti
2. La funzione presenta un asintoto verticale di equazione ...
a)
x=0
b)
x = -1
c)
d)
nessuno dei precedenti
3. La funzione ...
a)
interseca l'asse x solo nel punto (1/2,0)
b)
interseca l'asse x nei punti (1,0) e (3/2,0)
c)
interseca l'asse x nel punto (0,0)
d)
non interseca l'asse x
4. In quale tra gli insiemi proposti, la funzione risulta positiva?
a)
b)
c)
d)
nessuno dei precedenti
Nella figura è rappresentata la funzione
1. Quale tra gli insiemi proposti è il suo dominio?
a)
b)
c)
d)
nessuno dei precedenti
2. La funzione presenta un asintoto verticale nel punto x=0
a)
VERO
b)
FALSO
3. La funzione ...
a)
interseca l'asse x nel punto (0,0)
b)
interseca l'asse x nel punto (1,0)
c)
interseca l'asse x nel punto (-1,0)
d)
non interseca l'asse x
4. In quale tra gli intervalli proposti, la funzione risulta positiva?
a)
b)
c)
d)
nessuno dei precedenti
5. A quale valore corrisponde il limite infinito della funzione:
a)
0
b)
c)
d)
nessuno dei precedenti
Nella figura è rappresentata la funzione
1. Quale tra gli insiemi proposti è il suo dominio?
a)
b)
c)
d)
nessuno dei precedenti
2. La funzione presenta un asintoto verticale nel punto x = - 5
a)
VERO
b)
FALSO
3. La funzione ...
a)
interseca l'asse x nel punto (- 4,0)
b)
interseca l'asse x nel punto (4,0)
c)
interseca l'asse x nel punto (- 4,0) e (4,0)
d)
non ínterseca l'asse x
4. In quale tra gli insiemi proposti, la funzione risulta positiva?
a)
b)
c)
nessuno dei precedenti
d)
5. A quale valore corrisponde il limite destro della funzione:
a)
0
b)
nessuno dei precedenti
c)
d)
Nella figura è rappresentato un ramo della funzione
1. Quale tra gli insiemi proposti è il suo dominio?
a)
b)
c)
d)
2. La funzione presenta un asintoto verticale nel punto x = 3
a)
VERO
b)
FALSO
3. La funzione ...
a)
interseca l'asse x nel punto (- 3,0)
b)
interseca l'asse x nel punto (3,0)
c)
interseca l'asse x nel punto (- 3,0) e (3,0)
d)
non interseca l'asse x
4. In quale tra gli insiemi proposti, la funzione risulta negativa?
a)
b)
mai
c)
sempre
d)
nessuno dei precedenti
5. A quale valore corrisponde il limite sinistro della funzione:
a)
3
b)
c)
d)
nessuno dei precedenti
STUDIO DI FUNZIONE RAZIONALE FRATTA
Passo dopo passo
y=
f ( x)
g ( x)
CALCOLO CAMPO D’ESISTENZA
Il campo di esistenza è sempre ∀x ∈ R − { g ( x) = 0}
Quindi la prima cosa da fare è porre g ( x) ≠ 0 e trovare le soluzioni che non si annullano. Queste
soluzioni vanno inserite nella parentesi graffa
POSITIVITA’ DELLA FUNZIONE ( y >0)
f ( x)
>0.
g ( x)
Poiché è una fratta, allora bisogna applicare la regola del segno e cioè
f ( x) > 0
Bisogna porre tutta la funzione y =
g ( x) > 0
Conosciute le soluzioni delle due singoli funzioni, si mettono insieme tali soluzioni e si vede dove la
f ( x)
ha segno positivo (positività della funzione) e dove invece ha segno meno
funzione y =
g ( x)
(funzione che passa per il campo negativo)
LIMITI
Bisogna calcolare i seguenti limiti:
1.
2.
lim y = ...
x →+∞
lim y = ...
x →−∞
Ricorda che per x → ±∞ devo vedere il grado delle funzioni f ( x) e g ( x)
• Se il grado della funz. f è maggiore del grado della funz. g allora il limite è ±∞
• Se il grado della funz. f è minore della funz. g allora il limite è 0
• Se i gradi delle funzioni sono uguali allora si prende il coefficiente (numero) che sta
davanti alla x di grado maggiore (della funz. f) e quello che sta davanti alla x di grado
maggiore (della funz. g). Il risultato è il numero che è rapporto dei due coefficienti.
3.
Ricorda che:
+n
= +∞
0+
lim
x → punti _ discontinuità
−n
= +∞
0−
y = ...
−n
= −∞
0+
+n
= −∞
0−
ASINTOTI
1. Se il limite lim y = n (cioè la x va a ± ∞ mentre il risultato è un numero)
x →±∞
Allora la funzione ha un ASINTOTO ORIZZONTALE (la retta orizzontale y=n)
2. Se il limite lim y = ±∞ (cioè la x -> numero n mentre il risultato è ± ∞ )
x→n
Allora la funzione ha un ASINTOTO VERTICALE (x= n)
3. Se non esiste asintoto orizzontale, dobbiamo cercare un eventuale ASINTOTO
OBLIQUO. Se il limite:
lim
x →±∞
f ( x)
f ( x)
= m e lim
− mx = q (con m finito ≠ 0 e q finito)
x
→±∞
x ⋅ g ( x)
g ( x)
Allora la retta y = mx + q è un asintoto obliquo
MASSIMI E MINIMI ( y ' >0)
(crescenza e decrescenza)
f ( x)
(derivata del rapporto) e si pone il
g ( x)
risultato >0. Con la regola del segno, si vede dove la funzione y ' è positiva (crescenza
)e
dove è negativa (decrescenza
). Il punto valle è il minimo, il punto monte è il max.
Si calcola la derivata prima della funzione fratta
FLESSI ( y '' >0)
(concavità e convessità)
f ( x)
(derivata del rapporto) e si pone il
g ( x)
risultato >0. Con la regola del segno, si vede dove la funzione y '' è positiva (convessità
)
e dove è negativa (concavità
). Il punto valle o il punto monte è il flesso.
Si calcola la derivata seconda della funzione fratta