UNIVERSITÀ DEL SALENTO
FACOLTÀ DI SCIENZE MMFFNN
Corso di Laurea in Fisica
CORSO DI LABORATORIO I
a.a. 2015/2016
MISURA DELLA DENSITÀ DI UN SOLIDO GEOMETRICO
Scopo dell’esperienza
Misura della densità media alcuni corpi solidi di forma regolare tramite la misura del volume e
della massa.
Che cosa si intende per densità?
In che modo è possibile determinare la densità di un corpo solido?
Cenni teorici
La densità di un solido è definita dalla relazione:
ρ=
dM
dV
ovvero è la derivata della massa fatta rispetto al volume. Se il solido è omogeneo la relazione
precedente può essere scritta, più semplicemente come:
ρ=
M
V
L'esperienza consiste nel determinare separatamente la massa M dei campioni a disposizione e il
loro volume V.
Saranno inoltre eseguite le prime elaborazioni di dati sperimentali applicando la teoria degli errori
di misura e saranno discusse l'entità delle incertezze e le possibili cause.
Che tipo di incertezze si hanno nelle misure dirette?
Come si propagano le incertezze nelle misure indirette (volume e densità)?
Strumenti e materiale a disposizione
• Elencare la strumentazione ed il materiale a disposizione per eseguire la misura scopo
dell’esperienza.
In che modo si misura la massa? Che strumento si ha a disposizione? È adatto allo scopo? Che
caratteristiche ha?
In che modo si misura il volume? Che caratteristiche hanno i campioni? La forma geometrica è
regolare? La densità è omogenea? Si può determinare il volume mediante la misura delle dimensioni
lineari?
Che strumenti sono a disposizione? Sono tutti adatti allo scopo? Che caratteristiche hanno?
• Determinare l’intervallo di funzionamento, l’incertezza di sensibilità e l’unità di misura degli
strumenti a vostra disposizione
• Verificare con cura l’azzeramento. Se esso non è perfetto, prendere nota di questa “lettura
di zero” (essa, presa col suo segno algebrico, andrà sottratta a tutte le letture effettuate
con lo stesso strumento).
Misure dirette
• Misurare le diverse dimensioni lineari dei campioni a disposizione utilizzando per ogni
dimensione, in successione, tutti gli strumenti di misura nell’ordine dell’incertezza di
sensibilità decrescente.
• Annotare i valori misurati nelle tabelle con le relative incertezze.
I valori sono fra loro compatibili?
• Misurate la massa ed indicate la corrispondente incertezza.
Determinazione del volume e della densità (misure indirette)
• Determinare il volume dei campioni utilizzando di volta in volta le misure ottenute con lo
stesso strumento di misura (se una delle lunghezze risultasse al di fuori dell’intervallo di
funzionamento di uno degli strumenti, utilizzate per quella lunghezza la migliore delle
stime ottenute con uno degli altri strumenti).
• Stimare l’incertezza sul volume facendo ricorso alla teoria della propagazione delle
incertezze.
• Scrivere il valore del volume con il numero corretto di cifre significative.
• Determinare quindi il valore della densità del campione a vostra disposizione.
• Stimare l’incertezza sulla densità facendo ricorso alla teoria della propagazione delle
incertezze.
• Scrivete il risultato della misura con il numero corretto di cifre significative.
Commenti e discussione
1. Confrontando i valori ottenuti di densità con i valori riportati in tabella, è possibile fare
delle ipotesi sul materiale di cui sono costituiti i campioni?
2. I risultati sperimentali sono compatibili entro le incertezze di misura con i valori tabulati?
UNIVERSITÀ DEL SALENTO
FACOLTÀ DI SCIENZE MMFFNN
Corso di Laurea in Fisica
CORSO DI LABORATORIO I
a.a. 2015/2016
MISURA DEL PERIODO DI OSCILLAZIONE DI UN
PENDOLO SEMPLICE E STIMA DEL VALORE DI g
Scopo dell’esperienza
Misura del periodo di oscillazione di un pendolo semplice, studio della dipendenza del periodo di
oscillazione dalla lunghezza del filo e stima del valore dell’accelerazione di gravità.
Che cosa si intende per pendolo semplice?
L’azione di quali forze determina il moto di un pendolo?
Che tipo di moto è?
Da che cosa dipende il periodo di oscillazione?
Cenni teorici
Il pendolo semplice consiste di una piccola sfera appesa ad un centro di sospensione O mediante un
filo inestensibile di massa trascurabile. La configurazione di equilibrio del pendolo è quella nella
quale il centro di sospensione O, il filo teso ed il centro della sferetta sono allineati lungo la
verticale (volgarmente configurazione del filo a piombo). Se al filo teso allontaniamo la sferetta
dalla posizione di equilibrio, lasciandola libera essa inizia ad oscillare attorno a questa posizione in
un piano verticale. L’ampiezza delle oscillazioni è individuata dall’angolo α compreso tra la
verticale ed il filo.
Nel limite delle piccole oscillazioni (α≤5°) il moto del pendolo semplice è un moto armonico di
periodo indipendente dall'ampiezza α (legge dell'isocronismo delle piccole oscillazioni) e dalla
massa del pendolo. Il periodo di oscillazione dipende invece dalla lunghezza l del pendolo con una
legge data dalla relazione:
T = 2π
l
g
dove g rappresenta l’accelerazione di gravità.
L'esperienza consiste nella misura di T al variare della lunghezza del pendolo, l, e nella
determinazione di g sfruttando la relazione che lega T ad l.
Strumenti e materiale a disposizione
• Elencare la strumentazione ed il materiale a disposizione per eseguire la misura scopo
dell’esperienza.
In che modo si realizza un pendolo semplice? Che caratteristiche ha?
In che modo si misura il periodo di oscillazione? E la lunghezza del pendolo?
Che strumenti sono a disposizione? Sono adatti allo scopo? Che caratteristiche hanno?
• Determinare l’intervallo di funzionamento, l’incertezza di sensibilità e l’unità di misura degli
strumenti a vostra disposizione.
Operazioni preliminari
• Posizionare l’asta in modo tale che possa servirvi da riferimento per rilasciare il pendolo
sempre con il medesimo scostamento angolare di circa 5°.
Il periodo di oscillazione del pendolo dipende dallo scostamento iniziale?
Ha senso fissare lo scostamento angolare a circa 5°? Perché?
Determinazione del valore dell’accelerazione di gravità
• Sospendere il pendolo al telaio in modo tale che esso abbia una lunghezza iniziale di circa
50 cm.
• Effettuare accuratamente la misura della lunghezza stessa.
• Mettere in oscillazione il pendolo e misurare il tempo τ che impiega per compiere n = 10
oscillazioni complete.
• Scrivere il valore di τ con l’incertezza associata.
• Determinare T e scriverne il valore con la rispettiva incertezza (calcolata usando la
propagazione delle incertezze).
Perché è consigliabile determinare T tramite la misura di τ?
• Ripetere la misura 5 volte.
• Determinare la media aritmetica e l’incertezza associata al valor medio di T.
Perché è consigliabile ripetere più volte la misura di T?
• Variare la lunghezza del pendolo e ripetere le misure del periodo di oscillazione.
• Annotare in una tabella i valori di l e di Tmedio con le relative incertezze.
• Riportare i dati sperimentali (con le barre d’errore) in un grafico con l sull’asse x e Tmedio
sull’asse y.
La relazione fra T ed l sembra essere lineare?
Sulla base delle informazioni teoriche che tipo di relazione esiste fra T ed l? È possibile linearizzare
la funzione che descrive la relazione fra T ed l?
• Calcolare T2 e la relativa incertezza (mediante la propagazione delle incertezze).
• Annotare in una tabella i valori di l e di (Tmedio)2 con le relative incertezze.
• Riportare i dati sperimentali (con le barre d’errore) in un grafico con l sull’asse x e (Tmedio)2
sull’asse y.
La relazione fra T 2 ed l sembra essere lineare?
• Determinare la retta che meglio approssima i dati sperimentali (retta di BEST FIT) mediante
il metodo della massima e minima pendenza.
Qual è il valore del coefficiente angolare della retta di BEST FIT?
Qual è il valore dell’incertezza sul coefficiente angolare della retta di BEST FIT?
• Scrivere il coefficiente angolare della retta di BEST FIT con l’incertezza associata e con il
corretto numero di cifre significative.
La retta passa per l’origine?
Esiste una relazione che lega il coefficiente angolare della retta trovata al valore dell’accelerazione
di gravità locale g?
• Determinare il valore di g dal valore del coefficiente angolare della retta di BEST FIT.
• Determinare l’incertezza associata a g mediante la propagazione delle incertezze.
• Scrivere il valore finale di g con l’incertezza associata ed il numero corretto di cifre
significative.
Il valore sperimentale è compatibile con il valore atteso di g = (9.81±0.01) m/s 2 ?
•
Provare ad eseguire il FIT utilizzando il programma Root.
Il coefficiente angolare ottenuto con Root è compatibile con quello ottenuto graficamente (metodo
della massima e minima pendenza)?
Misure ripetute
• Fissare la lunghezza del pendolo ad un valore a scelta fra quelli utilizzati nella prima parte
dell’esperienza.
• Mettere in oscillazione il pendolo e misurare il tempo τ che impiega per compiere n = 10
oscillazioni complete.
• Scrivere il valore di τ con l’incertezza associata.
• Determinare T e scriverne il valore con la rispettiva incertezza (calcolata usando la
propagazione delle incertezze).
• Ripetere la misura in modo da ottenere un totale di circa 80 misure.
Qual è la migliore stima del periodo?
Ha senso calcolare la semi dispersione massima?
Che incertezza va associata?
Che tipo di incertezza è?
• Calcolare il valore medio, la deviazione standard, la deviazione standard della media e
scrivere il valore del periodo con l’incertezza statistica associata (con il corretto numero di
cifre significative).
Commenti e discussione
È stato raggiunto lo scopo dell’esperienza?
È stata verificata la legge teorica che lega lunghezza e periodo di un pendolo semplice?
È stato determinato il valore dell’accelerazione di gravità?
Il risultato ottenuto è compatibile con il valore atteso entro gli errori sperimentali?
Ha senso aumentare il numero di misure? Perché?
UNIVERSITÀ DEL SALENTO
FACOLTÀ DI SCIENZE MMFFNN
Corso di Laurea in Fisica
CORSO DI LABORATORIO I
a.a. 2015/2016
MISURA DELLA COSTANTE ELASTICA DI UNA MOLLA E
VERIFICA DELLA LEGGE DI HOOKE
Scopo dell’esperienza
Misura della costante elastica di una o più molle e verifica della legge di Hooke.
Che cosa stabilisce e in quali condizioni vale la legge di Hooke?
Che cos’è la costante elastica di una molla?
In che modo è possibile determinare sperimentalmente la costante elastica di una molla?
Cenni teorici
Applicando ad un corpo una forza, esso si deforma. Se il corpo ritorna alla forma iniziale quando
l’azione della forza cessa, le deformazioni sono dette elastiche e vale la legge di Hooke, secondo la
quale la deformazione è proporzionale alla forza applicata.
La legge di Hooke vale per piccole deformazioni fino al limite di elasticità della molla, oltre il quale
le deformazioni divengono permanenti.
Indicando con ∆l = l – l0 la variazione di lunghezza della molla dovuta ad una forza F (con l0
lunghezza a riposo ed l lunghezza della molla sottoposta a sollecitazione), entro la regione di
elasticità della molla si ha:
F = k ∆l (legge di Hooke)
La costante di proporzionalità k è detta costante elastica della molla e dipende dal materiale di cui
è costituita, dal diametro e dal numero di spire.
Nell’esperienza si studierà la deformazione di una o più molle elicoidali allo scopo di verificare la
validità della legge di Hooke e di determinare la costante elastica mediante due metodi (statico e
dinamico).
Infatti la costante elastica di una molla può essere determinata sperimentalmente misurando le
elongazioni ∆l al variare delle forze applicate. Se all’estremità inferiore di una molla sospesa
verticalmente è appesa una massa m, la forza applicata coincide con la forza peso della massa e la
legge di Hooke si riscrive nel seguente modo:
mg = k ∆l = k (l – l0)
Che tipo di misure è opportuno eseguire per determinare la costante elastica di una molla mediante
la legge di Hooke?
Come è possibile valutare la dipendenza dell’allungamento della molla dalla forza ad essa applicata?
Inoltre, se la massa m viene spostata dalla sua posizione di equilibrio di una distanza x, su di essa
agirà una forza di richiamo della molla pari a F’ = -kx.
L’equazione del moto sarà del tipo:
m
d 2x
= −kx
dt 2
e descriverà un moto armonico di periodo
T = 2π
m
k
Dalla misura della massa appesa e del periodo di oscillazione è possibile determinare k.
In effetti, questa soluzione vale nel caso di molle ideali, ossia di molle di massa nulla. Nel caso
reale, detta M la massa della molla, il periodo risulterà pari a:
T = 2π
m+
M
3
k
Che tipo di misure è opportuno eseguire per determinare la costante elastica di una molla mediante
il metodo delle oscillazioni?
Strumenti e materiale a disposizione
• Riflettendo sul tipo di misure da eseguire, elencare la strumentazione ed il materiale a
disposizione.
• Determinare l’intervallo di funzionamento, l’incertezza di sensibilità e l’unità di misura degli
strumenti a vostra disposizione
In che modo si misura la forza applicata (massa)? Che strumento si ha a disposizione? È adatto allo
scopo? Che caratteristiche ha?
In che modo si misura l’allungamento? Che strumento si ha a disposizione? È adatto allo scopo? Che
caratteristiche ha?
In che modo si misura il periodo? Che strumento si ha a disposizione? È adatto allo scopo? Che
caratteristiche ha?
Oltre alla strumentazione, quale altro materiale è necessario per effettuare le misure?
Misure
Metodo statico
• Per ogni molla annotare inizialmente la lunghezza a riposo (con l’incertezza associata).
• Misurare l’allungamento per almeno 5 valori della massa sospesa (di cui sia stato annotato
il valore misurato con la rispettiva incertezza) all’estremità libera, avendo l’accortezza di
rispettare il carico massimo ammissibile.
• Riportare in una tabella i dati di m ed l con le rispettive incertezze.
• Riportare i dati sperimentali su un grafico di l in funzione di m con le barre di errore.
I dati sperimentali sembrano legati da una legge di tipo lineare (vale la legge di Hooke)?
• Determinare la retta che meglio approssima i dati sperimentali (retta di BEST FIT) mediante
il metodo della massima e minima pendenza.
Qual è il valore del coefficiente angolare della retta di BEST FIT?
Qual è il valore dell’incertezza sul coefficiente angolare della retta di BEST FIT?
• Scrivere il coefficiente angolare della retta di BEST FIT con l’incertezza associata e con il
corretto numero di cifre significative.
La retta passa per l’origine?
Che cosa rappresenta l’intercetta? È compatibile con il valore misurato della lunghezza a riposo l 0 ?
• Confrontare i valori della lunghezza a riposo della molla e dell’intercetta con le rispettive
incertezze e dire se i valori sono compatibili.
Esiste una relazione che lega il coefficiente angolare della retta trovata con la costante elastica
della molla?
• Determinare la costante elastica della molla dal valore del coefficiente angolare assumendo
come valore dell’accelerazione di gravità locale g = (9.81±0.01) m/s2.
• Determinare l’incertezza associata alla costante elastica mediante la propagazione delle
incertezze.
• Scrivere il valore finale della costante elastica della molla con l’incertezza associata ed il
numero corretto di cifre significative.
•
Provare ad eseguire il FIT utilizzando il programma Root.
Il coefficiente angolare ottenuto con Root è compatibile con quello ottenuto graficamente (metodo
della massima e minima pendenza)?
Metodo dinamico
• Appendere ad una molla una massa (di cui sia stato annotato il valore misurato con la
rispettiva incertezza).
• Spostare la massa dalla sua posizione di equilibrio ed osservare le modalità con cui oscilla la
molla.
• Se le oscillazioni sono sufficientemente regolari, misurare il tempo necessario a compiere
una decina di oscillazioni (con la rispettiva incertezza).
• Determinare il valore del periodo (con la rispettiva incertezza).
• Ripetere la misura 5 volte.
• Determinare il valor medio del periodo e l’incertezza associata.
• Determinare la costante elastica della molla dalla relazione che la lega al periodo di
oscillazione.
• Valutare mediante la propagazione delle incertezze, l’indeterminazione da associare alla
costante elastica.
• Confrontare i valori (con le rispettive incertezze) delle costanti elastiche valutati per la
stessa molla e verificare se sono compatibili.
Commenti e discussione
È stato raggiunto lo scopo dell’esperienza?
È stata verificata la legge di Hooke?
Sono state determinate le costanti elastiche delle molle a disposizione?
I risultati ottenuti con i diversi metodi per ogni singola molla sono compatibili?
UNIVERSITÀ DEL SALENTO
FACOLTÀ DI SCIENZE MMFFNN
Corso di Laurea in Fisica
CORSO DI LABORATORIO I
a.a. 2015/2016
VERIFICA DELLE LEGGI DEL MOTO RETTILINEO
UNIFORMEMENTE ACCELERATO
Scopo dell’esperienza
Analisi del moto di un corpo sottoposto a forze costanti e misura dell’accelerazione.
Che cosa è il moto uniformemente accelerato?
In che modo si può realizzare in laboratorio un esperimento per studiare il moto uniformemente
accelerato?
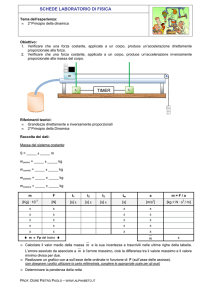
L’esperienza si propone di studiare il moto di un carrello in movimento su una rotaia, trascinato da
alcuni pesi in caduta vincolata.
L'apparato sperimentale, schematizzato in figura, è composto da un supporto che regge la rotaia,
sulla quale si muove il carrello, M, e la carrucola, nella cui gola viene fatto passare il filo che
applica la forza di trazione al carrello mediante alcune masse tarate, m.
L’apparato sperimentale è corredato di due fotocellule collegate ad un cronometro digitale e di un
elettromagnete con interruttore, che comanda lo sganciamento del carrello.
La misura consiste nella determinazione del tempo che il carrello impiega a percorrere distanze
prefissate, s, e nella verifica che i punti sperimentali ottenuti siano in accordo con la dipendenza
dello spazio dal tempo che, secondo la cinematica, è di moto uniformemente accelerato (legge
oraria del moto):
1
s (t ) = s0 + v0t + at 2
2
dove s(t) rappresenta la posizione del carrello all’istante t, s0 la posizione iniziale, v0 la velocità
iniziale ed a l’accelerazione, che, in un moto uniformemente accelerato, è costante.
Quali sono le forze che agiscono sul carrello?
Quali sono le forze che agiscono sulle masse appese al filo?
In che modo è possibile determinare l’accelerazione del carrello?
Cenni teorici
Un semplice modello, apparentemente appropriato a descrivere il moto del carrello, lo si ottiene
assimilando il carrello ad un punto materiale di massa M, libero di muoversi senza attrito lungo un
asse orizzontale, trascurando l'attrito agente sul perno della carrucola ed il momento di inerzia
della stessa, considerando il filo privo di massa, perfettamente flessibile ed inestensibile, e
trascurando la resistenza opposta al moto dall'aria.
Se il modello fosse adeguato, sospendendo all'estremità del tratto verticale del filo una massa m,
dall’analisi delle forze in gioco sull’intero sistema, risulterebbe che il carrello dovrebbe muoversi di
moto uniformemente accelerato con accelerazione data da:
a=
m
g
M +m
dove g = (9.81±0.01) m/s2 indica l'accelerazione di gravità.
Strumenti e materiale a disposizione
• Elencare la strumentazione ed il materiale a disposizione per eseguire la misura scopo
dell’esperienza.
Che caratteristiche ha l’apparato sperimentale?
Che tipo di misure si devono eseguire?
Di quali strumenti si ha bisogno?
In che modo si misura lo spazio s?
E i tempi di percorrenza?
È necessario misurare le masse dei campioni sospesi e del carrello?
Che strumenti sono stati messi a disposizione? Sono adatti allo scopo? Che caratteristiche hanno?
• Determinare l’intervallo di funzionamento, l’incertezza di sensibilità e l’unità di misura degli
strumenti a vostra disposizione.
Operazioni preliminari
• Verificare l'orizzontalità della rotaia.
Perché è importante verificare l’orizzontalità della rotaia?
Misure
• Posizionare la prima fotocellula proprio a ridosso del carrello bloccato dall'elettromagnete.
Perché si fissa il carrello a ridosso della fotocellula?
• Collegare il carrello al filo e far passare il filo nella gola della carrucola, facendo attenzione
che il filo in tensione sia orizzontale e che il carrello si possa muovere liberamente senza
impedimenti.
• Appendere al gancio legato all'altra estremità del filo i campioni dopo averne misurato la
massa.
• Posizionare la seconda fotocellula ad una data distanza.
• Misurare il tempo di percorrenza della distanza fissata.
• Ripetere la misura 5 volte.
I valori misurati del tempo sono compatibili entro le incertezze sperimentali?
Ha senso effettuare più misure?
Qual è la migliore stima del tempo di percorrenza di una data distanza? E quale incertezza va ed
essa associata?
Possiamo fare lo stesso discorso per le masse dei campioni sospesi?
Che tipo di incertezza va associata alla massa?
• Determinare la media dei tempi misurati e l’errore associato.
• Ripetere la misura cambiando per almeno 5 volte la distanza.
• Riportare in una tabella i valori misurati delle masse, delle distanze percorse e i tempi medi
(con le rispettive incertezze associate).
• Riportare i dati sperimentali (con le barre d’errore) in un grafico con s sull’asse x e Tmedio
sull’asse y.
La relazione fra T ed s sembra essere lineare?
Sulla base delle informazioni teoriche che tipo di relazione ci si aspetta fra T ed s?
È possibile linearizzare la funzione che descrive la relazione fra T ed s?
• Calcolare T2 e la relativa incertezza (mediante la propagazione delle incertezze)
• Annotare in una tabella i valori di s e di (Tmedio)2 con le relative incertezze.
• Riportare i dati sperimentali (con le barre d’errore) in un grafico con s sull’asse x e (Tmedio)2
sull’asse y.
La relazione fra T 2 ed sl sembra essere lineare?
I dati ottenuti sono in accordo con la dipendenza spazio-temporale del moto uniformemente
accelerato nel caso particolare in cui s 0 e v o sono nulli?
• Determinare la retta che meglio approssima i dati sperimentali (retta di BEST FIT) mediante
il metodo della massima e minima pendenza.
Qual è il valore del coefficiente angolare della retta di BEST FIT?
Qual è il valore dell’incertezza sul coefficiente angolare della retta di BEST FIT?
• Scrivere il coefficiente angolare della retta di BEST FIT con l’incertezza associata e con il
corretto numero di cifre significative.
La retta passa per l’origine?
Il valore dell’incertezza è compatibile con 0?
Esiste una relazione che lega il coefficiente angolare della retta trovata il valore dell’accelerazione
del carrello?
• Determinare il valore di dell’accelerazione del carrello dal valore del coefficiente angolare
della retta di BEST FIT.
• Determinare l’incertezza associata all’accelerazione mediante la propagazione delle
incertezze.
• Scrivere il valore finale dell’accelerazione con l’incertezza associata ed il numero corretto di
cifre significative.
• Determinare il valore dell’accelerazione mediante la relazione
a=
m
g
M +m
• Determinare il valore dell’incertezza mediante la propagazione delle incertezze.
Il valore sperimentale ottenuto dalla retta di BEST FIT è compatibile con quello ricavato usando il
modello semplificato del moto del carrello?
• Confrontare i due valori ottenuti dell’accelerazione del carrello e dire se entro le incertezze
sperimentali sono compatibili.
• Provare ad eseguire il FIT utilizzando il programma Root.
Il coefficiente angolare ottenuto con Root è compatibile con quello ottenuto graficamente (metodo
della massima e minima pendenza)?
• Provare a ripetere le misure con una massa sospesa diversa.
Il modello teorico semplificato si adatta meglio al sistema nel caso in cui la massa sospesa è
maggiore? Perché?
Commenti e discussione
È stato raggiunto lo scopo dell’esperienza?
È stata verificata la legge oraria del moto uniformante accelerato?
È stato determinato il valore dell’accelerazione del carrello sottoposto a forza costante?
Il valore ottenuto sperimentale è compatibile con il valore atteso secondo il modello proposto?
UNIVERSITÀ DEL SALENTO
FACOLTÀ DI SCIENZE MMFFNN
Corso di Laurea in Fisica
CORSO DI LABORATORIO I
a.a. 2015/2016
MISURA DI LUNGHEZZE ED ANALISI STATISTICA
Scopo dell’esperienza
Determinazione della migliore stima dello spessore di un campione di dadi per bulloni.
Premessa
Si suppone che i dadi per bulloni, di cui si vuole determinare lo spessore, siano stati prodotti dalla
stessa macchina impostata con parametri prefissati; ossia che gli elementi di ciascun gruppo di
dadi abbiano nominalmente tutti lo stesso spessore. Eseguendo le misurazioni dello spessore x dei
dadi (sulla superficie piana delle corone circolari) con un calibro Palmer è possibile evidenziare
eventuali fluttuazioni.
L’esperienza ha l’obiettivo di determinare la migliore stima dello spessore dei dadi mediante la
rappresentazione grafica dei dati, il calcolo dell’incertezza nelle misure ripetute e il confronto dei
valori sperimentali con quelli nominali.
Come è possibile valutare la migliore stima dello spessore dei dadi?
Quale incertezza attribuire?
Il valore ottenuto sperimentalmente può essere accettato senza riserve?
Strumenti e materiale a disposizione
• Riflettendo sul tipo di misure da eseguire, elencare la strumentazione ed il materiale a
disposizione.
• Determinare l’intervallo di funzionamento, l’incertezza di sensibilità e l’unità di misura degli
strumenti a vostra disposizione.
In che modo si misura lo spessore dei dadi? Che strumento si ha a disposizione? È adatto allo
scopo? Che caratteristiche ha?
Esecuzione dell’esperienza
• Utilizzare un campione di n = 30 dadi di un unico tipo ed annotare il tipo di dadi usato (serie
1, serie 2, serie 3).
• Misurare con lo strumento a disposizione gli spessori xi, effettuando tre misure per ogni
dado su differenti punti della superficie
• Riportare in una tabella gli N = 3n i valori misurati (indicando l’incertezza associata).
Mediante quali parametri è conveniente caratterizzare la serie di dati a disposizione?
• Calcolare e scrivere (con le corrette unità di misura): 1) la media aritmetica, 2) la varianza
empirica, 3) la deviazione standard empirica (s) e 4) la deviazione standard empirica della
media relativa agli N valori registrati.
Che informazioni forniscono la media e le deviazioni standard?
Come è possibile rappresentare graficamente i dati sperimentali?
La variabile-spessore è discreta o continua?
Conviene usare un diagramma a barre o un istogramma?
.
Cenni teorici
La distribuzione degli N valori ottenuti può essere rappresentata graficamente mediante un
istogramma riportando in ascisse i valori di x suddivisi in K intervalli di ampiezza opportuna tali che
∆xk ≥ 2∆x
con ∆x incertezza di sensibilità dello strumento e disegnando rettangoli di base ∆xk e altezza
uguale al numero Fk delle misure il cui valore è compreso nell’intervallo k-esimo (frequenza
assoluta) (prendere ∆xk = costante) o alla frequenza relativa
f rk =
Fk
N
o ancora alla densità di frequenza
fk =
f rk
Fk
=
∆xk N∆xk
• Ordinare i dati sperimentali in ordine crescente di spessore.
• Individuare l’intervallo in cui cadono i dati sperimentali.
• Dividere l’intervallo totale in K intervalli di ampiezza ∆xk .
•
Riportare in una tabella gli intervalli scelti (classi) ed in corrispondenza di ogni classe il
numero di dati che cadono nella suddetta classe (frequenza assoluta, Fk), la frequenza
relativa, frk, e la densità di frequenza, fk.
• Costruire l’istogramma dei risultati ottenuti rappresentando sull’asse delle ascisse le classi
ed in ordinata le densità di frequenza.
Che andamento presenta l’istogramma?
Ha la tipica forma a campana?
La scelta della classi è stata opportuna? Oppure conviene diminuire o aumentare il numero di
classi?
Supponendo che i dadi utilizzati per le misure possono essere pensati costituire un campione della
popolazione di tutti i dadi prodotti dalla macchina e che la distribuzione sia descrivibile da una
distribuzione Gaussiana
−
1
f X ,σ ( x ) =
e
2π σ
( x − X )2
2σ 2
X= x e σ=s
con
•
Calcolare la probabilità che una misurazione dia luogo a un valore x tale che
x − 0.01mm ≤ x ≤ x + 0.01mm
In che modo è possibile valutare la probabilità che il valore di una misura cada in un intervallo
prestabilito?
Conviene utilizzare la variabile standardizzata z?
Come si definisce la variabile standardizzata z?
Come si ridefinisce il problema di valutare la probabilità che il valore di una misura cada in un
intervallo se si utilizza la variabile standardizzata z?
•
Scrivere la variabile standardizzata z relativa alla variabile x = spessore dei dadi.
•
Calcolare i valori di z (za e zb) in corrispondenza degli estremi dell’intervallo
[ x − 0.01mm, x + 0.01mm]
•
Calcolare la probabilità che
z a ≤ z ≤ zb
Come si calcola la probabilità z a ≤ z ≤ z b ?
•
Utilizzando la tabella con valori della distribuzione normale standard cumulativa, calcolare
la probabilità richiesta.
È possibile sfruttare le proprietà di simmetria della funzione f(z)?
Infine supponendo che il valore medio della popolazione dei dadi sia:
X = 7.81 mm (per i dadi tipo 1),
X = 11.75 mm (per i dadi tipo 2),
X = 15.49 mm (per i dadi tipo 3)
•
Determinare la compatibilità del valore medio del campione di laboratorio con il valore
medio della popolazione dei dadi a cui il campione appartiene.
In che modo è possibile valutare la compatibilità del valore della media misurato con quello della
popolazione?
•
Valutare la discrepanza fra valore misurato e valore atteso, normalizzata alla deviazione
standard della media.
•
Utilizzando la tabella con valori della distribuzione normale standard cumulativa, valutare
la probabilità che la discrepanza sia maggiore della discrepanza calcolata.
•
Fissare un livello di significatività e dire se il risultato è accettabile (ovvero se la probabilità
che la discrepanza sia maggiore della discrepanza calcolata è al di sopra del valore di
significatività stabilito).
Commenti e discussione
È stato raggiunto lo scopo dell’esperienza?
La rappresentazione grafica dei dati è un modo adeguato per interpretare con immediatezza i dati
sperimentali?
La distribuzione sperimentale è interpretabile con una funzione Gaussiana?
Il valor medio misurato è compatibile con quello atteso?