Schemi a blocchi Sistema in serie

Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Schemi a blocchi
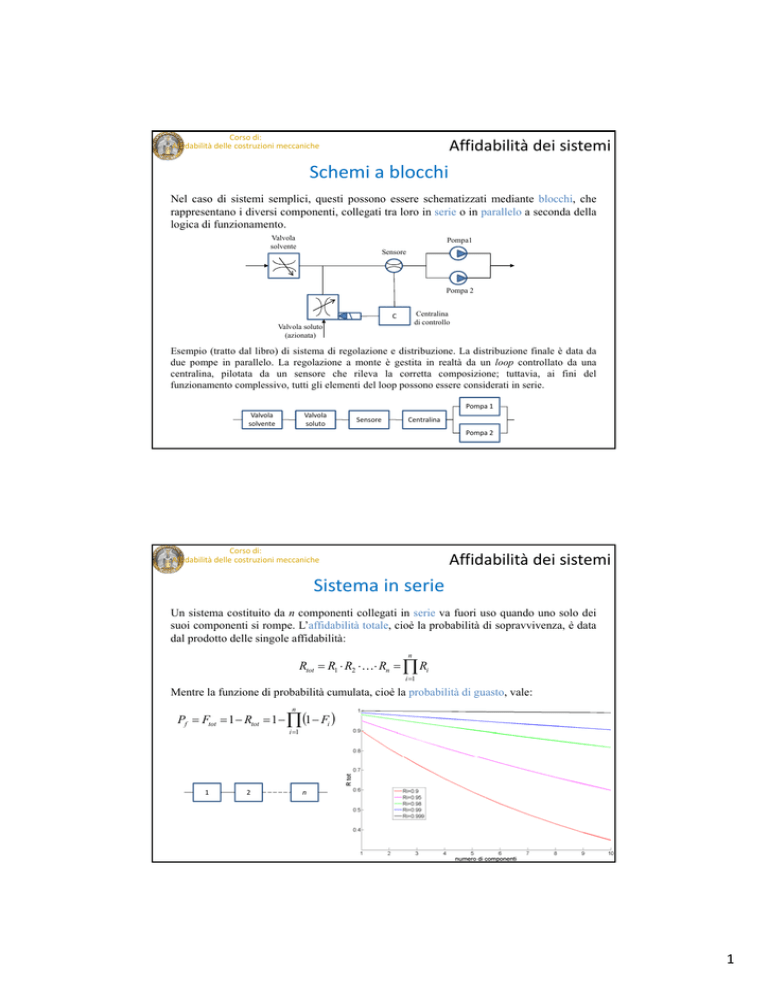
Nel caso di sistemi semplici, questi possono essere schematizzati mediante blocchi, che
rappresentano i diversi componenti, collegati tra loro in serie o in parallelo a seconda della
logica di funzionamento.
Vl l
Valvola
solvente
Pompa1
Sensore
Pompa 2
Centralina
di controllo
C
Valvola soluto
(azionata)
Esempio (tratto dal libro) di sistema di regolazione e distribuzione. La distribuzione finale è data da
due pompe in parallelo. La regolazione a monte è gestita in realtà da un loop controllato da una
centralina, pilotata da un sensore che rileva la corretta composizione; tuttavia, ai fini del
funzionamento complessivo, tutti gli elementi del loop possono essere considerati in serie.
Pompa 1
Valvola solvente
Valvola soluto
Sensore
Centralina
Pompa 2
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Sistema in serie
Un sistema costituito da n componenti collegati in serie va fuori uso quando uno solo dei
suoi componenti si rompe. L’affidabilità totale, cioè la probabilità di sopravvivenza, è data
dal prodotto delle singole affidabilità:
n
Rtot  R1  R2  Rn   Ri
i 1
Mentre la funzione di probabilità cumulata, cioè la probabilità di guasto, vale:
n
Pf  Ftot  1  Rtot  1   1  Fi 
i 1
1
2
n
1
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Sistema in serie
Se tutti i componenti sono descritti da distribuzioni esponenziali negative, con parametri λi,
allora il sistema complessivo è descritto ancora da una esponenziale negativa:
n
Rtot  R1  R2  Rn   Ri
n
t 
Rtot   eit  e  i
i 1
Ri  eit
i 1
…con parametro λtot pari alla somma dei vari λi
h  tot   i   hi
Il tasso di guasto sarà dunque:
Il MTTF sarà dunque:


0
0
MTTF   Rtot dt  
..cioè
 R dt  
i

0
et  i dt 
1
 i
e 
t 
0

1
 i

1
tot
1
1

MTTFtot
MTTFi
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Sistema in serie
Se invece i componenti sono descritti da distribuzioni generiche (non exp. neg.),
l’affidabilità complessiva è ancora data per definizione da:
n
Rtot  R1  R2  Rn   Ri
i 1
Questa volta però il MTTF non è esplicitabile in forma semplice:

MTTF   Rtot dt
0
ad esempio
Il tasso di guasto medio per un sistema costituito da
elementi in serie può essere calcolato come la somma
dei singoli tassi di guasto medi
htot   hi
1 exp
2 weib
htot  1  h2
Per componenti descritti da distribuzioni dei Weibull, il tasso di guasto medio durante
un periodo di durata t è calcolabile come:
h
1 t
1 t   
h d    

0
t
t 0   
 1

1 t
t  1
d      
t  

2
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Sistema in parallelo
Un sistema costituito da n componenti collegati in parallelo va fuori uso quando tutti i suoi
componenti si rompono. La probabilità di cedimento del sistema è data dal prodotto delle
singole probabilità di rottura (in quanto eventi indipendenti) :
n
Pf  Ftot  F1  F2  Fn   Fi
i 1
n
1  Rtot  1  R1   1  R2   1  Rn    1  Ri 
i 1
Mentre la funzione di affidabilità, vale:
n
n
i 1
i 1
Rtot  1   Fi  1   1  Ri 
1
2
n
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Sistema in parallelo
Si nota come aumentando il numero di
componenti in parallelo, l’affidabilità
cresce rapidamente.
Purtroppo però aumentano anche i costi
del sistema.
Una configurazione tipica è quella di
avere due componenti uguali di cui uno in
stand-by.
stand-by
1
switch
2
Svantaggi:
-Occorrono ispezioni periodiche del componente in stand-by
-L’affidabilità complessiva è fortemente condizionata da quella dello switch
3
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Sistema in parallelo
Il MTTF è espresso da: MTTF 


0
dove Rtot  1 
Rtot dt
n
n
i 1
i 1
 Fi  1   1  Ri 
Nel caso n componenti in parallelo descritti da distribuzioni esponenziali negative, con
parametri λi, il MTTF complessivo si calcola nel seguente modo:


n
 

MTTF   1   1  eit  dt
0
 i 1

Ri  eit
Nel caso di 2 soli componenti in parallelo descritti da distribuzioni esponenziali negative,
si ha:

 


MTTF   1  1  e1t  1  e2t dt 
0
1

1
1 2
Corso di:
Affidabilità delle costruzioni meccaniche

1
1  2
Affidabilità dei sistemi
Esercizio
Calcolare l’affidabilità complessiva dei due sistemi rappresentati
A
B
C
RA  0.9
RB  0.4
A
B
C
RC  0.75
Calcolare l’affidabilità complessiva dei due sistemi rappresentati considerando un aumento
del 5% dell’affidabilità degli elementi A e B (alternativamente)
4
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Calcolo del tasso di guasto
Ricordando la definizione
f t  
ht  
f t 
Rt 
ht   
d
d
F t    Rt 
dt
dt
1 d
Rt 
Rt  dt
Nel caso di 2 componenti in serie si ha: Rtot t   R1 t   R2 t 
d
dR t 
dR t 
Rtot t   1 R2 t   2 R1 t    f1 t R2 t   f 2 t R1 t 
dt
dt
dt
htot t   
d
f t R2 t   f 2 t R1 t  f1 t  f 2 t 
Rtot t   1


 h1 t   h2 t 
Rtot t  dt
R1 t R2 t 
R1 t  R2 t 
1
I tassi di guasto si sommano
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Calcolo del tasso di guasto
Ricordando la definizione
f t  
ht  
f t 
Rt 
d
d
F t    Rt 
dt
dt
ht   
1 d
Rt 
Rt  dt
Nel caso di 2 componenti in parallelo si ha: Rtot t   1  F1 t   F2 t 
d
dF t 
dF t 
Rtot t    1 F2 t   2 F1 t    f1 t F2 t   f 2 t F1 t 
dt
dt
dt
htot t   
f t F t   f 2 t F1 t 
1 d
Rtot t   1 2
Rtot t  dt
1  F1 t F2 t 
I tassi di guasto non si moltiplicano
5
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Calcolo del tasso di guasto
Esempio con 2 componenti distribuiti secondo esponenziali negative
λ1 = 1/200 [h], λ2 = 1/100 [h] -> MTTF 1 = 200 [h], MMTF 2 = 100 [h]
MTTF S ≈ 67.2 [h], MMTF P ≈ 232.5 [h]
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Calcolo del tasso di guasto
Esempio con 2 componenti distribuiti secondo Weibull
α1 = 100 [h], β1 = 0.8, α 2 = 400 [h], β 2 = 2.5 -> MTTF 1 = 113.4 [h], MMTF 2 = 355.4 [h]
MTTF S ≈ 97.6 [h], MMTF P ≈ 371.3 [h]
6
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Esercizio
Calcolare l’affidabilità ed il tasso di guasto del sistema rappresentato per l’istante di tempo
t = 1500 h
f A  N 1000,400
A
f B  W 800,2.3
C
fC  E0.0005
B
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
FMEA
La tecnica FMEA (Failure Mode & Effect Analysis) è stata sviluppata per evidenziare i
modi di guasto, classificandoli in base a 3 indici da 1 a 10:
1) Severità: indica la gravità del guasto
2) Occorrenza: indica la probabilità o frequenza di accadimento
3) Rilevabilità: indica la possibilità di rilevare il (potenziale) guasto prima che accada
Il prodotto dei 3 indici prende il nome di Risk Priority Number (RPN) e rappresenta
l’ordine di priorità con il quale cercare di rimediare ai guasti.
Si arriva quindi a tabelle di questo tipo:
Nome e/o
Nome e/o
numero parte
Funzione
Modo o causa Modo
o causa
di guasto
Severità
Occorrenza
Rilevabilità
RPN
Azioni
correttive
1
2
…
7
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
FMEA
Nome
parte
Funzione
Piastra
Azionamento
tramite piede
Molla
Stelo
Richiamo verso
posizione chiusa
posizione
chiusa
Collegamento,
riduzione forza piede
Modo
di guasto
Causa
Effetto
Severità
Occorrenza
Rilevabilità
RPN
Esempio di FMEA per il pedale di acceleratore
Allentamento
Errato
dimensionamento
Rumore
1
1
2
2
Rottura
Materiale
difettoso
Disagio
2
1
1
2
Allentamento
Montaggio
difettoso
Disagio
3
3
2
18
Rottura
Fatica
Bloccaggio
8
1
9
72
Deformazione
Materiale
difettoso
Corso di:
Affidabilità delle costruzioni meccaniche
Bloccaggio
9
1
3
27
Disagio
2
2
2
8
Affidabilità dei sistemi
Albero dei Guasti
L’albero dei guasti (o Fault Tree Analysis FTA) è un particolare flow-chart atto a indicare le
probabilità di guasto e come sono associate tra loro, mettendo in evidenza le relazioni
causa-effetto. Andrebbe preceduto da un FMEA per conoscere tutti i componenti.
Si parte dal Top event, in cascata, fino a considerare tutti i possibili guasti
8
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Albero dei Guasti
L’albero dei guasti (o Fault Tree Analysis FTA) è un particolare flow-chart atto a indicare le
probabilità di guasto e come sono associate tra loro, mettendo in evidenza le relazioni
causa-effetto.
Si possono distinguere i seguenti componenti in un albero dei guasti:
1) Evento principale (Top Event)
Top Event
Evento base
2) Evento base, causato da un componente per il quale si può stabilire una
probabilità
3) Evento intermedio, causato da una combinazione di eventi base (tramite
porte logiche)
….
4) Evento non spiegato o non sviluppato in eventi base (soprattutto per
mancanza di info)
….
5) Porta AND, l’evento in uscita accade se accadono tutti gli eventi in input
6) Porta OR, l’evento in uscita accade se accade almeno uno degli input
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Albero dei Guasti
Valvola
solvente
Schema a blocchi
Pompa1
Sensore
Pompa 2
C
Valvola soluto
(azionata)
TOP EVENT
no erogazione
Centralina
di controllo
FTA
No solvente in circuito
Guasto valvola
Mancanza solvente
No soluto in circuito
Mancanza soluto
Guasto valvola
Guasto sensore
Blocco mandata
Guasto centralina
Guasto pompa 1
Guasto pompa 2
9
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Albero dei Guasti
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Esercizio
Ricavare lo schema a blocchi corrispondente ai seguenti FTA
Top Event
Top Event
<
Top Event
Top Event
A
1
B
2
3
A
4
1
B
2
3
4
10
Corso di:
Affidabilità delle costruzioni meccaniche
Affidabilità dei sistemi
Esercizio
Calcolare la probabilità di accadimento del Top Event
R1 = 0.95
R2 = 0.96
R3 = 0.7
R4 = 0.8
R5 = 0.9
R6 = 0.92
RB = 0.7
RD = 0.9
Top Event
H
A
1
K
2
3
E
D
C
B
5
4
Corso di:
Affidabilità delle costruzioni meccaniche
6
Affidabilità dei sistemi
RA = 0.86
RB = 0.92
RC = 0.85
RD = 0.9
RE = 0.95
RF = 0.96
RG = 0.97
RH = 0.98
Top Event
H
E
A
B
C
F
G
D
11