MATEMATICA - SECONDA LSA

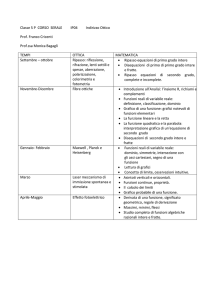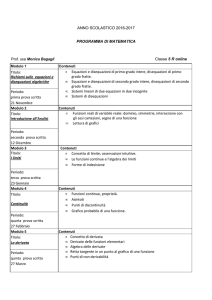
MATEMATICA - SECONDA LSA
CONTENUTI















Primi elementi di calcolo matriciale:
matrici quadrate di ordine 2
(facoltativamente: di ordine 3) a
entrate reali: somma, prodotto,
moltiplicazione per un numero reale;
determinante.
Semplici sistemi lineari 2×2 o 3×3 a
coefficienti costanti.
Proprietà fondamentali dei numeri
reali.
Radicali.
Equazioni e sistemi di secondo
grado.
Disequazioni algebriche intere e
fratte di primo e secondo grado.
Equazioni e disequazioni di grado
superiore al secondo binomie e
trinomie.
Sistemi di disequazioni algebriche
intere e fratte.
Elementi di geometria euclidea
piana: teoremi di Pitagora e di
Euclide; rotazioni;
teorema
di
Talete; similitudini.
Elementi di geometria analitica:
punti; punto medio; distanza fra
punti;
rette;
condizioni
di
parallelismo e perpendicolarità;
intersezione fra rette; distanza
punto-retta;
parabola;
rappresentazione di particolari
funzioni.
Teorema dei seni, teorema del
coseno. Funzioni circolari inverse:
definizione, uso applicativo.
Complementi sui vettori nel piano e
nello spazio: componente di un
vettore lungo un asse; componenti
rispetto alla base standard; prodotto
scalare e vettoriale.
Primi elementi di probabilità e
statistica.
Il concetto di modello matematico.
Introduzione a Cabri Géomètre,
Derive e Geogebra.
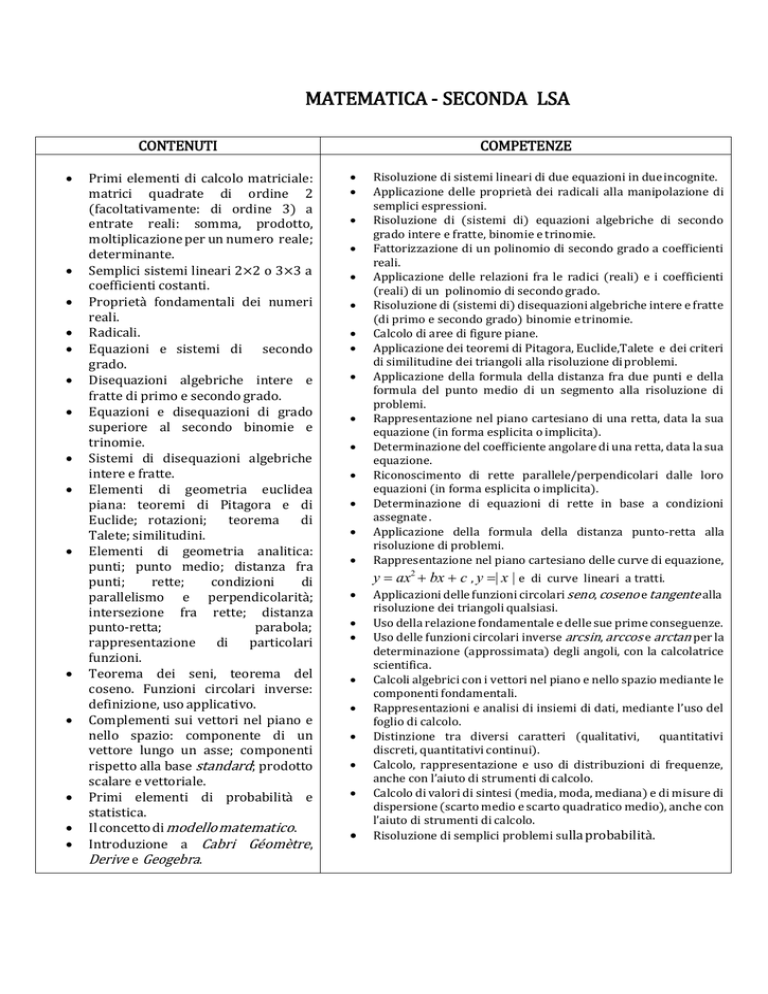
COMPETENZE















Risoluzione di sistemi lineari di due equazioni in due incognite.
Applicazione delle proprietà dei radicali alla manipolazione di
semplici espressioni.
Risoluzione di (sistemi di) equazioni algebriche di secondo
grado intere e fratte, binomie e trinomie.
Fattorizzazione di un polinomio di secondo grado a coefficienti
reali.
Applicazione delle relazioni fra le radici (reali) e i coefficienti
(reali) di un polinomio di secondo grado.
Risoluzione di (sistemi di) disequazioni algebriche intere e fratte
(di primo e secondo grado) binomie e trinomie.
Calcolo di aree di figure piane.
Applicazione dei teoremi di Pitagora, Euclide,Talete e dei criteri
di similitudine dei triangoli alla risoluzione di problemi.
Applicazione della formula della distanza fra due punti e della
formula del punto medio di un segmento alla risoluzione di
problemi.
Rappresentazione nel piano cartesiano di una retta, data la sua
equazione (in forma esplicita o implicita).
Determinazione del coefficiente angolare di una retta, data la sua
equazione.
Riconoscimento di rette parallele/perpendicolari dalle loro
equazioni (in forma esplicita o implicita).
Determinazione di equazioni di rette in base a condizioni
assegnate .
Applicazione della formula della distanza punto-retta alla
risoluzione di problemi.
Rappresentazione nel piano cartesiano delle curve di equazione,
y  ax2  bx  c , y | x | e di curve lineari a tratti.









Applicazioni delle funzioni circolari seno, coseno e tangente alla
risoluzione dei triangoli qualsiasi.
Uso della relazione fondamentale e delle sue prime conseguenze.
Uso delle funzioni circolari inverse arcsin, arccos e arctan per la
determinazione (approssimata) degli angoli, con la calcolatrice
scientifica.
Calcoli algebrici con i vettori nel piano e nello spazio mediante le
componenti fondamentali.
Rappresentazioni e analisi di insiemi di dati, mediante l’uso del
foglio di calcolo.
Distinzione tra diversi caratteri (qualitativi,
quantitativi
discreti, quantitativi continui).
Calcolo, rappresentazione e uso di distribuzioni di frequenze,
anche con l’aiuto di strumenti di calcolo.
Calcolo di valori di sintesi (media, moda, mediana) e di misure di
dispersione (scarto medio e scarto quadratico medio), anche con
l’aiuto di strumenti di calcolo.
Risoluzione di semplici problemi sulla probabilità.