FISICA SPERIMENTALE II!
ì Corso di laurea in Chimica (6CFU, 48 ORE)!
Docente: Claudio Melis, Ricercatore a tempo determinato presso
il Dipartimento di Fisica!
Email: [email protected]!
!
Telefono Ufficio :070 675 4929!
!
Pagina web: http://people.unica.it/claudiomelis/!
!
Orario di Ricevimento:Venerdì dalle ore 15:00 alle ore 17:00!
Presso il Dipartimento di Fisica, secondo piano torre C ufficio 24!
!
!
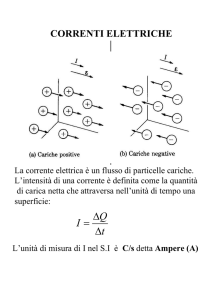
Corrente Elettrica !
Finora abbiamo considerato le cariche elettriche fisse: Elettrostatica
Consideriamole adesso in movimento !
La carica in moto forma una corrente elettrica.
L intensità di corrente è uguale al tasso (rapidità) con cui le cariche si
muovono attraverso una ipotetica sezione di un conduttore!
dq
i!
dt
La direzione della corrente è definita come la direzione in cui si muovono le
particelle cariche positivamente. Comunue, la corrente è uno scalare.!
ΔQ
ΔQ = n ⋅V ⋅ q = n ⋅ A ⋅ Δxl ⋅ q = n ⋅ A ⋅ vd ⋅ Δt ⋅ q ⇒ I =
= n ⋅ q ⋅ vd ⋅ A
Δt
Corrente Stazionaria (o continua) !
Una corrente elettrica la cui intensità non varia nel tempo.!
Una volta raggiunto lo stato stazionario, la corrente è la stessa
attraverso una qualunque sezione di un conduttore (continuità).!
La carica totale che passa attraverso una sezione in un intervallo di
tempo t è data da!
t
q = ∫ dq = ∫ idt = it
0
Unità SI : Ampere (A)!
1 A = 1 C/s!
Densità di Corrente!
La densità di corrente è un vettore.!
La direzione della densità di corrente in un
dato punto è la direzione in cui si
muove una carica positiva.!
L intensità della densità di corrente è tale
che la corrente totale attraverso una
sezione è data da!
! !
i = " J ! dA
!
se la corrente è uniforme e parallela a dA
i=
" J dA = J " dA = JA
#
Linee di flusso del
campo di corrente!
J =i A
Aspetti Microscopici!
Quanti elettroni mobili che ci sono in un conduttore ?!
Esempio – Il rame è utilizzato comunemente nell impianto elettrico delle
abitazioni. Quanti sono gli elettroni mobili che troviamo in un filo di rame ?!
La densità del rame è 8.95 g/cm3 ed il suo peso molecolare 63.5 g/mole (in
una mole di qualunque sostanza contiene un numero di atomi pari al numero
di Avogadro 6.02×1023 atomi. !
Nell ipotesi che vi sia un solo elettrone mobile per ciascun un atomo di rame:!
m
63.5 g
3
V = =
=
7.09
cm
! 8.95 g cm 3
N Av 6.02 !1023 elettroni
22 elettroni
28 elettroni
n=
=
=
8.49
!10
=
8.49
!10
V
7.09 cm 3
cm 3
m3
Aspetti Microscopici!
Le cariche mobili, cioè gli elettroni, si trovano nei conduttori con una densità, ne
(ne ≅ 1029 m-3)!
Il campo elettrico E mette in moto gli elettroni:!
– tutte le cariche si muovono con una
velocità, ve!
– gran parte del moto è di tipo
casuale (in tutte le direzioni on media
nulla) con una piccola velocità media
eguale a vd!
velocità di deriva
La velocità dovuta al moto casuale è
dell ordine di 106 m/s. Mentre, la velocità
di deriva è solo ≈10 -5 m/s.
Aspetti Microscopici!
Densità di Corrente, J, è data da J = qenevd!
– unità di J è C/m2sec ovvero Ampere/m2!
– la corrente, I, è J moltiplicato lʼarea della sezione,
p.es. I = J πr2 se circolare.!
Il campo E in un conduttore è generato da una batteria!
Le cariche sono messe in movimento, ma vengono diffuse
molto brevi da oggetti sul loro cammino!
– c è un grande affollamento all interno del metallo!
– difetti, vibrazioni reticolari, ecc.!
in tempi
Tipico tempo di diffusione τ = 10-14 sec!
le cariche sono accelerate durante questo tempo e, successivamente,!
diffuse casualmente!
Aspetti Microscopici!
A che velocità si muovono gli elettroni mobili ?!
Esempio – Un filo di rame ha una sezione di circa 5 mm2, se è attraversato
da una corrente di 10 A a che velocità media si muovono gli elettroni ?!
Noto il numero di elettroni liberi nel rame (vedi es. precedente), la velocità di
deriva vale: !
J
I
vd =
=
=
ne neA
=
10 C s
elettroni
−19
−6
2
8.49 × 10
×
1.6
×
10
C
×
5
×
10
m
m3
28
= 1.46 × 10
−4
m
s
Non sembra particolarmente elevata: ci vogliono circa 15000 sec per percorrere
1 metro (4 ore !!!).
Aspetti Microscopici!
la velocità media raggiunta in questo tempo è !
[ eE=forza, forza/m = a, v=at ]!
eEτ
F = ma ⇒ vd =
m
la densità di corrente è J = nevd , quindi la corrente è proporzionale
ad E che è proporzionale alla d.d.p.!
I ∝ J ∝ v ∝ E ∝ ΔV ⇒ ΔV = I ⋅ R
ΔV
1V
R=
resistenza ( unità di misura ohm , Ω ) 1Ω =
I
1A
In diversi casi R=cost al variare di V ⇒ Legge di OHM!
Legge di OHM non è una legge fondamentale della natura !!
Piuttosto è una relazione empirica valida soltanto per certi materiali e/o
dispositivi, in un campo limitato di condizioni !!
p.es. i semiconduttori, ed i dispositivi (diodo, transistor) sono non-ohmici!
Validità della legge di Ohm!
Un materiale conduttore obbedisce alla legge di Ohm quando la resistenza del
materiale è indipendente dall intensità e direzione del campo elettrico
applicato.!
ohmico!
Non-ohmico!
Aspetti Microscopici (definizioni)!
Sulla base delle relazioni precedenti possiamo riscrivere la legge
di OHM in forma microscopica (prescindendo dalla forma e
dimensioni del conduttore):!
! ! ne 2! $ !
!
!
J =#
& E ovvero J = ! E
" m %
Conducibilità
2
ne !
!=
m
Resistività
!
!
1
! = ! E = !J
!
Resistenza!
La resistenza è definita come il rapporto tra la d.d.p. applicata e la corrente che la a5raversa. V
R !
I
I
R
I
V
Unità: OHM = Ω
Effetto delle dimensioni
All
aumentare della lunghezza, R =!
L
A
il flusso di ele4roni è limitato All
aumentare dell
E j area della sezione il flusso è favorito Analogia (macroscopica) con il flusso di acqua in una condu4ura A L INTERPRETAZIONE MICROSCOPICA
DI R!
Microsc. una carica è ostacolata nel suo moto entro conduttore
1) Dalle altre cariche
2) Dai protoni dei nuclei
URTI dei portatori
di corrente contro
il reticolo cristallino
del conduttore!
DA COSA DIPENDE TALE
DIFFICOLTA ?!
E
misurata da R!
1) Caratt.fisiche del conduttore (tipo e
disposizione dei legami, dislocazione
dei nuclei)!
2) Lunghezza
l del conduttore (l ↑, R ↑)!
3) Sezione S del conduttore (S ↑, R↓)!
SECONDA LEGGE DI OHM!
l
R=ρ
S
ρ = RESISTIVITA del materiale (rende conto della
dip. di R dal materiale e dalla sua T)!
ρ dipende da T!
Resistività e coefficienti termici della
resistività per alcuni materiali:
!
Dipendenza di ρ da T Se T è alta, il materiale ha par?celle con grande agitazione termica à più difficile moto cariche all interno e quindi ρ deve aumentare ρ = ρ0(1+αT) URTI difficoltà nel moto à CAUSATA DA URTI fra le cariche e le particelle del
materiale!
URTO = DISSIPAZIONE DI ENERGIA (cfr. attrito!)!
Ecin_1 < Ecin_0!
Ecin_0!
prima!
Sezione cond.!
COSA IMPLICANO LE PERDITE DI ENERGIA? dopo!
URTI Necessità di ripris?nare con?nuamente ddp (un generatore SI SCARICA!) DISSIPAZIONI (ΔU < 0) EFFETTI TERMICI (macroscopici) dovu? a URTI (microscopici) EFFETTO JOULE DELLA CORRENTE!
L energia dissipata dalle cariche a causa degli urti, viene data alle particelle
del conduttore !
La carica perde
energia!
Sezione cond.!
Le partic. del mezzo sono
state urtate e hanno
RICEVUTO ENERGIA!
Le partic. del conduttore hanno ricevuto energia, incrementando U interna e
quindi T!
EFFETTO JOULE DELLA CORRENTE!
EFFETTO JOULE = effetto di
riscaldamento di un conduttore
percorso da corrente!
Macrosc. è dato dagli urti microscopici tra cariche in moto e
partic. del conduttore!
Un conduttore attraversato da corrente subisce un
incremento di T proporzionale alla sua resistenza R !
Funzionamento di phon, stufe elettriche…!
EFFETTO JOULE DELLA CORRENTE!
Per effetto Joule, alcuni conduttori, scaldandosi,
EMETTONO ANCHE RADIAZIONE VISIBILE!
Es. lampadina!!
EFFETTO JOULE DELLA CORRENTE!
Come MISURARE le dissipazioni?!
Calcolo il LAVORO DISSIPATO nell
di resistenza R dalla corrente I!
L = q·V!
L q ⋅V
P= =
t
t
attraversamento di un conduttore
Se ora divido per
t, ho POTENZA!
Ma q/t = I!
P = I ⋅V
EFFETTO JOULE DELLA CORRENTE!
P = V·I!
Se ora vale la prima legge di Ohm:!
V = R·I!
P =R ⋅ I
E
2
la potenza dissipata attraversando la resistenza R!
EFFETTO JOULE DELLA CORRENTE!
t
Se poi conosco il tempo di attraversamento , si ha:!
L = P·t = RI2 t!
Es. 1KWh = 3.600.000 J di energia elettrica in 1h di utilizzazione!!
Conoscendo la potenza in kW di un elettrodomestico, se conosco il
tempo di utilizzo, posso risalire al consumo in energia!!
esercizio!
esercizio!