visione stereoscopica

La percezione dello spazio:
visione stereoscopica
Corso di Principi e Modelli della Percezione
Prof. Giuseppe Boccignone
Dipartimento di Scienze dell’Informazione
Università di Milano
[email protected]
http://homes.dsi.unimi.it/~boccignone/GiuseppeBoccignone_webpage/Modelli_Percezione.html
La percezione dello spazio
//indizi binoculari
• Per ricostruire gli aspetti tridimensionali dell’ambiente il sistema visivo fa uso
di una serie di indizi di profondità.
• informazioni contenute nell’ambiente circostante.
• Distinguiamo fra:
• Indizi di profondità monoculari.
• Indizi di profondità binoculari.
• Tali indizi si combinano per fornire una rappresentazione coerente dello
spazio.
La percezione dello spazio
//indizi binoculari
• Avere due occhi invece comporta molti vantaggi:
1. un campo visivo più esteso
2. un sistema ridondante capace di permettere la visione anche nel caso che uno
dei due occhi venga gravemente danneggiato
3. poter ottenere sommazione binoculare
• Uno dei modi per ottenere indici di profondità dalle informazioni provenienti
dai due occhi è quello di considerare la geometria delle piccole differenze
nelle immagini retiniche (disparità binoculari) prodotte da gli stimoli visivi ad
una certa distanza dall’osservatore. Ciò permette la visione della profondità
tramite stereopsi
La percezione dello spazio
//indizi binoculari: visione stereoscopica
• Sommazione binoculare: vantaggio nel percepire gli oggetti fornito dal fatto di
avere due occhi invece di uno
• Disparità binoculare: differenza fra le immagini retiniche dei due occhi della
stessa immagine visiva.
• Stereopsi: una vivida impressione della tridimensionalità del mondo che non è
acquisibile attraverso la visione monoculare.
• dipende in parte dalla disparità binoculare
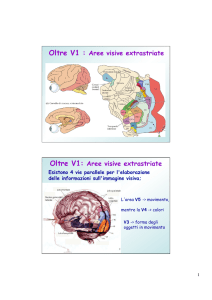
Visione stereoscopica:
// disparità binoculare
• Le immagini retiniche dei due occhi del mondo esterno non sono esattamente
le stesse!
immagine retinica destra
immagine retinica sinistra
Visione stereoscopica:
// disparità binoculare
• Il sistema visivo percepisce contemporaneamente due immagini retiniche
diverse
• Il risultato è che noi vediamo le due dita e il punto di fissazione a differenti
profondità nella spazio
• La disparità binoculare ha molto in comune con la parallasse di movimento:
• la parallasse di movimento confronta due diverse immagini retiniche in modo
sequenziale.
• la disparità binoculare due diverse immagini retiniche contemporanemente.
• Direzione e grandezza della disparità ci dicono quali punti sono vicini e quali
lontani
Visione stereoscopica:
// disparità binoculare: la corrispondenza
• Posizioni corrispondenti sulla retina:
• Posizioni sulla retina che coincidono se le due fovee sono sovrapposte.
• La disparità binoculare emerge quando un dato punto nell’ambiente esterno
proietta su punti differenti sulle due retine.
Visione stereoscopica:
// disparità binoculare: la corrispondenza
punto di fissazione
(centro fovea)
Visione stereoscopica:
// disparità binoculare: la corrispondenza
punto di fissazione
(centro fovea)
immagine retinica sinistra
punto di fissazione
(centro fovea)
immagine retinica destra
Visione stereoscopica:
// disparità binoculare: la corrispondenza
disparità = 0
punti retinici
corrispondenti
disparità non nulla
immagine retinica sinistra
immagine retinica destra
Visione stereoscopica:
// disparità binoculare: l’oroptere
• Non tutti i punti nell’ambiente producono disparità sulle retine destra e
sinistra.
immagine retinica sinistra
immagine retinica destra
• L’insieme dei punti che stimolano posizioni corrispondenti sulle due retine si
dice Oroptere.
• Dal punto di vista geometrico l’oroptere coincinde con il circolo di Vieth-Muller
Visione stereoscopica:
// disparità binoculare: l’oroptere
• Non tutti i punti nell’ambiente producono disparità sulle retine destra e
sinistra.
oroptere
• L’insieme dei punti che stimolano posizioni corrispondenti sulle due retine si
dice Oroptere.
• Dal punto di vista geometrico l’oroptere coincinde con il circolo di Vieth-Muller
Visione stereoscopica:
// disparità binoculare: l’oroptere
• L’insieme dei punti che stimolano posizioni corrispondenti sulle due retine si
dice Oroptere.
• Dal punto di vista geometrico l’oroptere coincinde con il circolo di Vieth-Muller
• Diplopia:
• Gli oggetti sull’oroptere vengono percepiti come oggetti singoli.
• Quelli sensibilmente più vicini o più lontani sono percepiti doppi.
Visione stereoscopica:
// disparità binoculare: diplopia
immagine
retinica
sinistra
immagine
retinica
sinistra
immagine
retinica
destra
immagine
retinica
destra
Visione stereoscopica:
// disparità binoculare: diplopia
Sx e Dx
disparità
nulla
Dx
Sx
disparità
grande
Sx e Dx
disparità
nulla
Dx
Sx
disparità
piccola
Visione stereoscopica:
// disparità binoculare: area di fusione di Panum
• L’insieme dei punti che stimolano posizioni corrispondenti sulle due retine si
dice Oroptere.
• Dal punto di vista geometrico l’oroptere coincinde con il circolo di Vieth-Muller
• Diplopia:
• Gli oggetti sull’oroptere vengono percepiti come oggetti singoli.
• Quelli sensibilmente più vicini o più lontani sono percepiti doppi.
• Gli oggetti che sono in prossimità dell’oroptere, tuttavia, possono essere
percepiti come unici.
• L’area dello spazio in cui è possibile la visione singola binoculare, ma che non
coincide geometricamentecon l’oroptere si dice Area di Fusione di Panum (Peter
Ludvig Panum 1820-1885)
Visione stereoscopica:
// disparità binoculare: segno
• La direzione della profondità è data dal segno della disparità
Disparità incrociata
occhio sx
punto a dx
occhio dx
punto a sx
Disparità non incrociata
occhio sx
punto a sx
occhio dx
punto a dx
Visione stereoscopica:
//stereoscopio
• Un macchinario per presentare due immagini diverse ai due occhi in modo da
ottenere una sola ed unica immagine tridimensionale (Sir Charles
Wheatstone)
Visione stereoscopica:
//stereoscopio
• Un macchinario per presentare due immagini diverse ai due occhi in modo da
ottenere una sola ed unica immagine tridimensionale (Sir Charles
Wheatstone)
Visione stereoscopica:
//stereoscopio
• Un macchinario per presentare due immagini diverse ai due occhi in modo da
ottenere una sola ed unica immagine tridimensionale (Sir Charles
Wheatstone)
Visione stereoscopica:
//stereogrammi
• Gli stereogrammi furono inventati sempre
da Charles Wheatstone nel 1838.
• Coppie di immagini che differiscono per il
posizionamento laterale relativo degli
elementi.
• Quando vengono viste
stereoscopicamente producono
un’illusione di profondità
• Gli stereogrammi “Random dot” possono
solo essere visti utilizzando indici di
profondità binoculari, essi infatti non
contengono indici di profondità monoculari
Visione stereoscopica:
//stereogrammi
Visione stereoscopica:
//stereogrammi
• Fusione libera: La tecnica di incrociare o divergere gli occhi in modo da
vedere uno stereogramma senza avere a disposizione uno stereoscopio
• Per fondere stereoscopicamente le due immagini è necessario sovrapporre le
due immagini percepite dai due occhi di modo che il cervello possa fonderle in
una.
• CONVERGENZA INCROCIATA (incrocio gli occhi).
• CONVERGENZA NON INCROCIATA (guardo l’immagine come se fissassi un punto
più lontano).
Visione stereoscopica:
//stereogrammi
Visione stereoscopica:
//stereogrammi
Visione stereoscopica:
//stereogrammi
• Se non ci riuscite.....STEREOCECITA’
• Non tutti percepiscono la profondità ottenuta dalla stereopsi, una condizione
conosciuta come stereocecità (stereoblindness)
• Una condizione di impossibilità di usare la stereopsi per vedere la profondità
• Ciò può esser causa per esempio di disturbi visivi patiti durante l’infanzia come
lo strabismo che consiste in un errato allineamento dei due occhi
Visione stereoscopica:
//stereogrammi di punti casuali (random dot)
• Bela Julesz (1971).
• La stereopsi può essere utilizzata per
individuare oggetti e superfici
nell’ambiente.
• Negli steregrammi di punti casuali noi
percepiamo una nuova immagine
tridimensionale, che non è rintracciabile
in nessuno delle due immagini fuse
• Gli stereogrammi con random dot
dimostrano che non è indispensabile
sapere quello che si sta osservando
prima di vedere l’immagine in profondità
tramite stereopsi. La sola disparità
binoculare è sufficiente per la percezione
della forma
Visione stereoscopica:
//stereogrammi di punti casuali
Visione stereoscopica:
//stereogrammi di punti casuali
Sinistra
Destra
Visione stereoscopica:
//stereogrammi di punti casuali
• Sir Charles Wheatstone dimostrò che la disparità binoculare è una condizione
necessaria alla stereopsi.
• Bela Julesz dimostrò che la disparità binoculare è anche condizione
sufficiente per la stereopsi
Visione stereoscopica:
//il problema della corrispondenza
• Il problema di trovare quale parte di una immagine nell’occhio sinistro deve
corrispondere ad una parte dell’immagine nell’occhio destro
• Problema: le immagini retiniche sono più numerose degli stimoli distali
Visione stereoscopica:
//il problema della corrispondenza
Visione stereoscopica:
//il problema della corrispondenza
ciò che vediamo
Visione stereoscopica:
//il problema della corrispondenza
1 2 3
ciò che vediamo
1
3
4
5
esistono due possibili interpretazioni
geometriche dello stimolo
Visione stereoscopica:
//il problema della corrispondenza
Cosa succede se l’immagine retinica sinistra del cerchio 2 viene messa in corrispondenza con
l’immagine retinica destra del cerchio 1 e l’immagine retinica sinistra del cerchio 3 viene messa
in corrispondenza con l’immagine retinica destra del cerchio 2?
1 2 3
1
3
4
5
• Si vedono quattro cerchi anziché tre, con i due centrali fluttuanti
Visione stereoscopica:
//il problema della corrispondenza: soluzione
• Il sistema visivo segue un’euristica: confronta
prima le due immagini foveali,poi quelle sulla
destra della fovea, infine quelle sulla sinistra
• Vincolo di unicità (Uniqueness constraint):
• un elemento dell’ambiente viene solitamente
rappresentato una sola volta in un immagine
retinica
• Vincolo di continuità (Continuity constraint) :
• i punti nell’ambiente che sono vicini ricadono
a distanze simili dell’osservatore - ad
eccezione dei bordi (in un mondo senza
porcospini)
Visione stereoscopica:
//il problema della corrispondenza: soluzione
• Questa soluzione non funziona per gli
stereogrammi a punti casuali.
• Il sistema visivo dovrebbe confrontare
centinaia di punti casuali identici fra
loro.
• Come potrebbe decidere che il punto
che cade in una regione della retina di
un occhio è proprio lo stesso che cade
in una regione della retina dell’altro
occhio??
Visione stereoscopica:
//il problema della corrispondenza: soluzione (2)
• Il sistema visivo filtra le immagini conservando solo le basse
frequenza spaziali.
• Procede ad un matching nel range delle basse frequenze spaziali
prima di passare a fare una analisi “fine” nello spettro delle frequenze
spaziali più alte
• In questo modo si ottiene una risposta approssimativa, ma sufficiente
a determinare una certa corrispondenza
Visione stereoscopica:
//il problema della corrispondenza: soluzione (2)
Visione stereoscopica:
//il problema della corrispondenza: soluzione (2)
Visione stereoscopica:
//rivalità binoculare
• Il sistema visivo è predisposto a risolvere le differenze fra l’informazione
proveniente dalle due retine.
• Tuttavia, cosa succede se presentiamo due stimoli diversi rispettivamente ai
due occhi?
• Provate a fissare un orologio da muro e poi ad alzare una mano fino ad
occludere con le dita l’oggetto nell!occhio destro.
• Vedete l’orologio o le vostre dita?
Visione stereoscopica:
//rivalità binoculare
• Quando le immagini proiettate dai due occhi sono sensibilmente differenti fra loro
si innesca una competizione fra i due flussi di informazione.
• L’informazione che vince diviene percezione cosciente.
• Questo fenomeno si dice rivalità binoculare.
• In realtà nessuna percezione vince la rivalità binoculare definitivamente
Visione stereoscopica:
//rivalità binoculare
Visione stereoscopica:
//rivalità binoculare
Visione stereoscopica:
//rivalità binoculare
Visione stereoscopica:
//rivalità binoculare
• La rivalità binoculare è un fenomeno comune
• sono molti gli stimoli che generano questo fenomeno.
• Tutto ciò che è fuori dall’area di fusione di Panum è soggetto a diplopia.
• In linea di massima, un oggetto fuori dall’area di Panum viene visto doppio e il
sistema visivo ne “sopprime” una copia.
Visione stereoscopica:
//il livello neurofisiologico
• Le info provenienti dai due occhi devono convergere nelle stesse cellule
• Molti neuroni binoculari rispondono in maniera ottimale quando le immagini
retiniche si trovano su punti corrispondenti delle due retine: Questa è la base
fisiologica dell’ horopter
• Molti altri neuroni binoculari rispondono in maniera ottimale quando la stessa
immagine occupa due punti leggeremente distinti sulle retine dei due occhi
(sono cioè regolati su una determinata disparità binoculare)
Visione stereoscopica:
//il livello neurofisiologico: area V1
• Singoli neuroni nella corteccia visiva
primaria (V1) e delle aree successive
a questa hanno campi recettivi che
coprono una regione di spazio
TRIDIMENSIONALE non solo
bidimensionale.
• alcuni neuroni rispondono ad una
ampia gamma di profondità ( per
esempio agli stimoli che stanno oltre
il punto di fissazione)
• altri molto più selettivi, rispondono a
stimoli ad un determinata profondità
ma non ad altre.
David Hubel and Torsten Wiesel
Visione stereoscopica:
//la corteccia striata: selezione informazione
Via magnocellulare:
localizzazione e
movimento
(dove)
Vie parvicellulare- blob:
percezione dei colori
e parvicellulare-interblob:
analisi delle forme
(cosa)
Vie binoculari
tridimensionalità
dell’oggetto
Visione stereoscopica:
//corteccia striata: neuroni insensibili alla disparità
Visione stereoscopica:
//la corteccia striata: neuroni sensibili alla disparità
Visione stereoscopica:
//la corteccia striata: neuroni sensibili alla disparità
neurone sensibile a disparità 0
Visione stereoscopica:
//la corteccia striata: neuroni sensibili alla disparità
neurone sensibile a disparità non crociata (far cell)
Visione stereoscopica:
//modelli computazionali
Ipotesi:
1.due camere con i loro assi
ottici paralleli e separati da una
distanza d detta baseline B
3.i fuochi alla stessa altezza
5.l'asse x del nostro sistema di
riferimento parallelo alla baseline
un qualsiasi punto nell'immagine
sinistra, questo avrà la stessa
ordinata nella corrispondente
immagine destra
Visione stereoscopica:
//modelli computazionali
il triangolo POF1 e' simile a F1O1P1
il triangolo POF2 e' simile a F2O2P
PO / F1O1 =
F1 F2 / (P1 O1+ O2 P2)
un qualsiasi punto nell'immagine
sinistra, questo avrà la stessa
ordinata nella corrispondente
immagine destra
Visione stereoscopica:
//modelli computazionali
PO / F1O1 =
F1 F2 / (P1 O1+ O2 P2)
distanza del punto dall'immagine / distanza focale =
Baseline / somma delle basi
H/f=
B / delta
Pixel!!!!!!!!!!!!!!!!!!!!!!! : 0,008333 mm
H = f * B / delta
nota
6 mm
nota corrispondenza?
12,8 mm
Pixel: 0,008333 mm
Visione stereoscopica:
//modelli: ricerca di punti significativi
Visione stereoscopica:
//modelli: ricerca delle corrispondenze
Visione stereoscopica:
//modelli: mappa di profondità
Visione stereoscopica:
//modelli: mappa di disparità
• In generale si cerca di risolvere le corrispondenze inferendo una mappa di
disparità D, osservando le immagini sinistra (left) e destra (right)
D
I= {IL, IR}
Visione stereoscopica:
//modelli: mappa di disparità
• Modello generativo probabilistico
D
D
P(D, I) = P(I | D) P(D)
= P(IL, IR | D) P(D)
I
I= {IL, IR}
Visione stereoscopica:
//modelli: mappa di disparità
• Inferenza con la regola di Bayes
P(D | I) =
P(IL, IR | D) P(D)
P(IL, IR )
D
max P(D | I) = max P(IL, IR | D) P(D)
• se P(D) = costante (e.g., uniforme)
max P(D | I) = max P(I | D)
= max !s e-F(s, d(s), I)
max log P(I | D)
min !s F(s, d(s), I)
I= {IL, IR}
Visione stereoscopica:
//modelli: mappa di disparità
• Minimizzazione di una funzione di costo
min !s F(s, d(s), I)
• Un esempio semplice:
• Per ogni punto dell’immagine di riferimento
• si confronta la finestra centrata sul punto corrente con tutte le finestre corrispondenti
nell’altra immagine che rientrano all’interno del range di disparità specifico per la
coppia stereo.
• il confronto si effettua usando come misura di matching la funzione SAD (Sum of
Absolute Differences) su pixel in scala di grigio.
• la finestra corrispondente al minimo della SAD determina la disparità per il punto
Visione stereoscopica:
//modelli: mappa di disparità
• Minimizzazione di una funzione di costo
min !s F(s, d(s), I)
dispMap=zeros(nrLeft, ncLeft); %mappa di disparità
win=(windowSize-1)/2;
%ciclo su tutti i pixel delle immagini IL IR
for(i=1+win:1:nrLeft-win)
for(j=1+win+dispMax:1:ncLeft-win)
prevSAD = 65532;
temp=0.0;
bestMatchSoFar = dispMin;
win
%per tutte le disparità ammissibili
for(dispRange=-dispMin:-1:-dispMax)
%CALCOLA LA DISPARITA A MINIMA SAD
sad=0.0;
for(a=-win:1:win)
leftImage
for(b=-win:1:win)
if (j-win+dispRange > 0)
temp=abs(leftImage(i+a,j+b)-rightImage(i+a,j+b+dispRange));
sad=sad+temp;
end
end
end
if (prevSAD > sad)
prevSAD = sad;
bestMatchSoFar = dispRange;
end
end
dispMap(i,j) = -bestMatchSoFar;
end
end
rightImage
Visione stereoscopica:
//modelli: mappa di disparità
mappa ideale
(ground truth)
mappa inferita
D
I= {IL, IR}
I= {IL, IR}
Percezione dello spazio
//conclusione: integrazione
Percezione dello spazio
Percezione dello spazio
//integrazione neurofisiologica
Percezione dello spazio
//integrazione: accoppiamento euristico
Percezione dello spazio
//integrazione: accoppiamento debole
Percezione dello spazio
//integrazione: accoppiamento debole/forte
Percezione dello spazio
//integrazione: accoppiamento forte