Numeri relativi e operazioni

Il termine algebra (dall'arabo, al-ğabr che significa
"unione", "connessione" o "completamento", ma anche
"aggiustare") deriva dal libro del matematico persiano
Muḥammad ibn Mūsā al-Ḵwārizmī, intitolato
Pagina di Algebra di al-Khwarizmi
Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa'lmuqābala
("Compendio
sul
Calcolo
per
Completamento e Bilanciamento"), conosciuto anche
nella forma breve Al-Kitab al-Jabr wa-l-Muqabala ,
che tratta la risoluzione delle equazioni di primo e di
secondo grado
Il merito di aver introdotto i numeri con segno va riconosciuto ai matematici
indiani e in particolare a BRAHMAGUPTA( VII sec. d.C.). La sua opera più
importante, Lilavati, rappresenta il primo esempio di aritmetica con i numeri
negativi. In essa compaiono infatti regole pratiche per l'addizione di crediti e
debiti, dove i debiti sono scritti preceduti da un punto per avvertire che il
valore deve essere considerato negativo.
Numeri relativi e operazioni
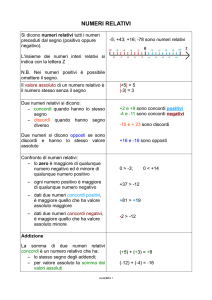
I numeri preceduti da un segno si dicono numeri relativi.
+9 e -5 sono numeri relativi
Il modulo o valore assoluto di un numero relativo è il numero stesso senza il segno.
Per indicare il modulo si usano due sbarrette verticali.
|+3|=|-3|= 3
Due numeri relativi si dicono concordi se hanno lo stesso segno.
+3 e +7 sono concordi
Due numeri relativi si dicono discordi se hanno segno diverso
+3 e -7 sono discordi
Due numeri relativi si dicono opposti se sono discordi e hanno lo stesso modulo.
+4 e -4 sono opposti
Confronto di numeri relativi
La loro rappresentazione sulla retta orientata dei numeri è la seguente:
Per confrontare due numeri relativi bisogna considerare la loro posizione sulla retta
orientata, osservando che i numeri sono disposti in modo crescente, (dal più piccolo al più
grande) e si è convenuto di chiamare positivo il verso da sinistra a destra e negativo quello
contrario.
Due numeri relativi si dicono uguali se hanno lo stesso segno e lo stesso modulo.
+4 e +4 sono uguali
Tra due numeri relativi discordi il maggiore è sempre quello positivo.
+4 > -3
Tra due numeri relativi positivi il maggiore è quello di maggiore valore assoluto.
+4 > +3 perché |+4|>|+3|
Tra due numeri relativi negativi il maggiore è quello di minore valore assoluto.
-3 > -4 perché |-3|<|-4|
Le operazioni
Addizione
La somma di due numeri relativi concordi è un numero che ha lo stesso segno degli addendi e
valore assoluto uguale alla somma dei loro valori assoluti
(+3)+(+4) = +7
(-2)+(-5) = -7
La somma di due numeri relativi discordi è un numero che ha il segno dell’addendo di valore
assoluto maggiore e valore assoluto uguale alla differenza dei loro valori assoluti.
(-3)+(+4) = +1
(+2)+(-5) = -3
+ perché |+4|>|-3|
- perché |-5|>|+2|
Regole di uso pratico
Un’utile regola di uso pratico, applicabile quando si deve calcolare la somma di più numeri
relativi, consente si eseguire la somma di tutti i numeri positivi e di quelli negativi e di seguire poi
la regola precedente per il calcolo della somma finale.
(+3)+(-2)+(+7)+(-9) = (+3)+(+7)+(-2)+(-9) = (+10)+(-11) = -1
In una somma le coppie di addendi opposti possono essere eliminate.
(+3)+(-5)+(-3)= -5
Un numero positivo può essere scritto benissimo senza segno.
Si può ricorrere alla scrittura semplificata di una somma algebrica trasformandola in
un’espressione con soli segni + e – semplicemente ricordando che una parentesi preceduta dal
segno + può essere eliminata.
(+4)+(+3) = 4 + 3
(+5)+(-7) = 5 – 7
7 + (4 –2 + 3) = 7 + (+ 4 – 2 + 3) = 7 + 4 - 2 + 3
Sottrazione
La differenza tra due numeri relativi è il numero che si ottiene sommando al minuendo
l’opposto del sottraendo.
In altre parole la sottrazione può essere ricondotta a un’addizione.
(-7) - ( +5 ) = ( -7) + ( -5 ) = +12
( +8 ) - ( - 14 )= (+8 )+ (+14) = +22
Regole di uso pratico
Si può ricorrere alla scrittura semplificata di una differenza algebrica trasformandola in
un’espressione con soli segni + e – semplicemente ricordando che una parentesi preceduta dal
segno - può essere eliminata cambiando di segno tutti i suoi termini.
(+4) - (+3) = 4 – 3
(+5) - (-7) = 5 + 7
7 - (4 – 2 + 3) = 7 - (+ 4 – 2 + 3) = 7 - 4 + 2 - 3
SOMMA ALGEBRICA TRA NUMERI RELATIVI
Parlando della differenza di numeri relativi abbiamo detto che essa è riconducibile ad una
addizione. Per questa ragione le operazioni di addizione e di sottrazione di numeri relativi
costituiscono un'unica operazione detta somma algebrica di numeri relativi.
Moltiplicazione
Si distinguono due casi: se i numeri relativi sono concordi o se sono discordi.
1) NUMERI RELATIVI CONCORDI:
Il prodotto algebrico di due numeri relativi concordi è un numero positivo che ha per modulo il
prodotto dei moduli.
Esempi:
( + 7 ) · ( + 4 ) = + 28
( – 7 ) · ( – 4 ) = + 28
2) NUMERI RELATIVI DISCORDI:
Il prodotto algebrico di due numeri relativi discordi è un numero negativo che ha per modulo il
prodotto dei moduli.
Esempi:
( + 7 ) · ( – 4 ) = – 28
( – 7 ) · ( + 4 ) = – 28
Pertanto, il prodotto algebrico tra due numeri relativi si base sulla seguente regola dei segni:
+·+=+
–·–=+
+·– =–
–·+ =–
CONCORDI = +
DISCORDI = –
Osservazioni:
Per ottenere il prodotto di più numeri relativi si trova il prodotto dei moduli (valori assoluti) dei
fattori e si dà il segno + o – se i fattori negativi sono in numero pari o dispari.
Esempi:
( – 2 ) · ( – 4 ) · ( – 3 ) = – 24
( – 2 ) · ( – 4 ) · ( – 3 ) · ( – 5 ) = + 120
Divisione
Il quoziente di due numeri relativi è un numero relativo che ha valore assoluto uguale al
quoziente dei valori assoluti e segno positivo se i termini dell’operazione sono concordi e segno
negativo se i termini dell’operazione sono discordi
Esempi:
( -12 ) : ( -3 ) = +4
(+20 ) : ( +4 ) = +5
( -18 ) : ( +9 ) = - 2
POTENZA DI NUMERI INTERI RELATIVI
Si distinguono due casi: se la base è un numero relativo positivo o negativo.
1) NUMERO RELATIVO POSITIVO:
Il risultato di una potenza di un numero relativo positivo è un numero positivo che ha per modulo
la potenza del modulo.
Esempi:
2
( + 5 ) = ( + 5 ) · ( + 5 ) = + 25
( + 5 )3 = ( + 5 ) · ( + 5 ) · ( + 5 ) = + 125
4
( + 5 ) = ( + 5 ) · ( + 5 ) · ( + 5 ) · ( + 5 ) = + 625
2) NUMERO RELATIVO NEGATIVO:
Il risultato di una potenza di un numero relativo negativo è un numero che ha per modulo la
potenza del modulo, mentre il segno è + se l’esponente è pari, mentre il segno è – se l’esponente è
dispari.
Esempi:
2
(–2) =(–2)·(–2)=+4
( – 2 )3 = ( – 2 ) · ( – 2 ) · ( – 2 ) = – 8
4
( – 2 ) = ( – 2 ) · ( – 2 ) · ( – 2 ) · ( – 2 ) = + 16
( – 2 )5 = ( – 2 ) · ( – 2 ) · ( – 2 ) · ( – 2 ) · ( – 2 ) = – 32