Esercizi svolti sulle leggi di Kirchhoff e potenze

Esercizi sulle leggi di Kirchhoff e sulle potenze
Esercizio n°1
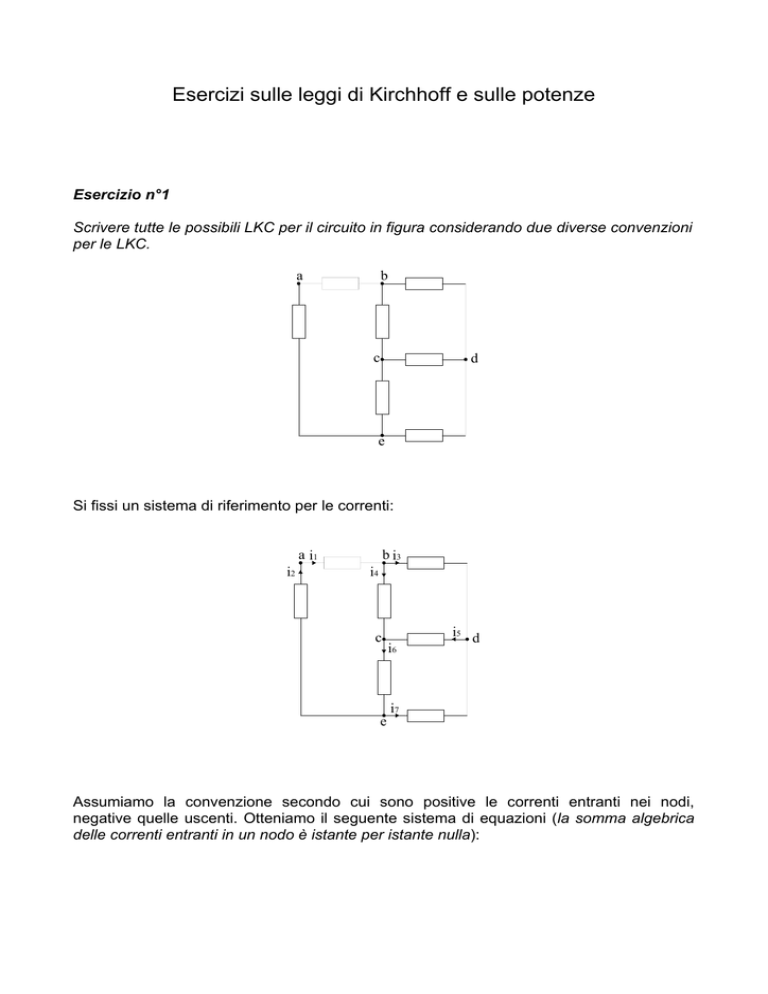
Scrivere tutte le possibili LKC per il circuito in figura considerando due diverse convenzioni
per le LKC.
a
b
c
d
e
Si fissi un sistema di riferimento per le correnti:
a i1
i2
b i3
i4
c
i6
i5 d
i7
e
Assumiamo la convenzione secondo cui sono positive le correnti entranti nei nodi,
negative quelle uscenti. Otteniamo il seguente sistema di equazioni (la somma algebrica
delle correnti entranti in un nodo è istante per istante nulla):
nodo a:
i2 − i1 = 0
nodo b:
i1 − i4 − i3 = 0
nodo c:
i 4 + i5 − i 6 = 0
nodo d:
i3 + i 7 − i5 = 0
nodo e:
i6 − i 2 − i 7 = 0
(*)
Assumiamo ora la convenzione secondo cui sono positive le correnti uscenti dal nodo e
negative quelle entranti (la somma algebrica delle correnti uscenti da un nodo è istante per
istante nulla). Otteniamo il seguente sistema di equazioni:
nodo a:
− i2 + i1 = 0
nodo b:
− i1 + i4 + i3 = 0
nodo c:
− i 4 − i5 + i 6 = 0
nodo d:
− i3 − i 7 + i5 = 0
nodo e:
− i6 + i 2 + i7 = 0
(**)
Il sistema (**) può essere ottenuto dal sistema (*) moltiplicando ogni equazione per -1. I
due sistemi sono quindi equivalenti, cioè ammettono la stessa soluzione. Ciò è necessario
in quanto i due sistemi descrivono lo stesso circuito con lo stesso sistema di riferimento
delle correnti (è cambiata la convenzione sui segni delle correnti ma non il sistema di
riferimento).
Esercizio n°2
Dato il circuito in figura, dimostrare che è ia = ib .
1
ia
N
2
3
ib
4
Fissiamo un sistema di riferimento per le correnti:
1
ia
i2
i1
N
i3
2
ib
3
i4
4
i5
Scriviamo la LKC in corrispondenza di ciascun nodo assumendo positive le correnti
uscenti da un nodo (la somma algebrica delle correnti uscenti da un nodo è istante per
istante nulla).
nodo 1:
− ia + i1 + i2 = 0
nodo 2:
− i1 + i3 − i4 = 0
nodo 3:
− i 2 − i3 + i5 = 0
nodo 4:
ib + i 4 − i5 = 0
Sommando membro a membro le equazioni del sistema si ha:
− i a + ib = 0
⇒
i a = ib
Un altro modo più generale di esprimere la LKC consiste nel definire una superficie
gaussiana (superficie chiusa) ed una convenzione per le correnti:
La somma algebrica di tutte le correnti che fuoriescono dalla (o entrano nella) superficie
gaussiana è istante per istante nulla
Fissiamo una superficie gaussiana come quella indicata in figura e assumiamo come
positive le correnti entranti nella superficie:
1
ia
i2
i1
N
i3
2
3
i4
ib
4
i5
Σ
Le sole correnti che attraversano le gaussiana sono ia e ib per cui possiamo scrivere
con la convenzione delle correnti positive entranti nella superficie Σ :
i a − ib = 0
⇒
i a = ib
Esercizio n°3
Dato il circuito in figura, ricavare le correnti i1 e i2.
a i2
b
i3
i3 = 4 A
c
i4
i1
i5
e
d
i4 = 1 A
i5 = 3 A
f
Con il fissato sistema di riferimento per le correnti, scriviamo le LKC nei nodi a e d
(occorrono due equazioni ):
nodo a:
i 2 + i 5 = i3
nodo d:
i4 + i5 + i2 = i1
Si tratta di un sistema di due equazioni nelle due incognite i1 e i2, che possiamo risolvere
col metodo di sostituzione:
i2 + 3 = 4
⇒
1 + 3 + i2 = i1
i2 = 1 A
, i1 = 5 A
Esercizio n°4
Dato il circuito in figura:
1
2
B
A
C
3
D
E
4
scrivere tutte le possibili LKT, avendo fissato un sistema di riferimento per le tensioni di
lato e il verso di percorrenza delle maglie.
Successivamente si valutino le tensioni vB e vE, nel caso in cui vA = 2V, vC = 5V, vD = 4V.
Fissiamo un sistema di riferimento per le tensioni di lato come indicato in figura:
1
2
B
A
C
3
D
E
4
e disegnamo le diverse maglie che si possono individuare nel circuito, per ciascuna delle
quali fissiamo arbitrariamente un verso di percorrenza:
1
1
2
B
A
2
B
3
A
C
C
3
3
D
E
E
D
4
4
4
maglia 1
maglia 2
maglia 3
Scriviamo la LKT per ciascuna maglia (la somma algebrica delle tensioni di lato è nulla istante
per istante):
maglia 1: − v A − v B − vC + v D = 0
maglia 2: v A − v E + vC + v B = 0
maglia 3: v D − v E = 0
A questo punto sostituiamo i valori delle tensioni date per ricavare quelli delle tensioni
incognite:
− 2 − vB − 5 + 4 = 0
v B = −3V
2 − vE + 5 + vB = 0
⇒
v E = 4V
4 − vE = 0
Esercizio n°5
Dato il circuito in figura:
1
B
A
2
3
D
F
C
5
G
4
E
H
e fissato il nodo 5 come riferimento, si scrivano le tensioni di lato in funzione delle tensioni
nodali riferite al nodo 5. Si valutino inoltre le tensioni di lato sapendo che e1 = 4V, e2 = 5V,
e3 = 8V, e4 = 10V, e5 = 0V.
Per tensione nodale di un nodo si intende la tensione nodo-nodo tra il nodo in questione e
quello di riferimento.
Fissiamo un sistema di riferimento per le tensioni di lato come indicato in figura:
1
B
A
2
D
C
3
F
5
E
G
4
H
Si può dimostrare infatti che la tensione tra una generica coppia di nodi k e j del circuito e
pari alla differenza delle rispettive tensioni nodali:
v kj = ek − e j
In particolare quindi anche la tensione di lato, che è una tensione nodo-nodo tra il nodo
supposto a tensione maggiore (+) e l’altro, si può esprimere in funzione delle tensioni
nodali dei nodi che rappresentano i vertici del lato.
Possiamo quindi scrivere le seguenti relazioni:
v A = e1 − e5 = e1
v E = e 4 − e5 = e 4
v B = e2 − e1
v F = e3 − e 4
v C = e 2 − e5 = e 2
v G = e3 − e 4
v D = e3 − e 2
v F = e 4 − e5 = e 4
Sostituendo i valori dati otteniamo:
v A = e1 − e5 = 4V
v E = e4 − e5 = e4 = 10V
v B = e2 − e1 = 5 − 4 = 1V
v F = e3 − e4 = 8 − 10 = −2V
vC = e2 − e5 = e2 = 5V
vG = e3 − e4 = 8 − 10 = −2V
v D = e3 − e2 = 8 − 5 = 3V
v F = e4 − e5 = e4 = 10V
Esercizio n°6
Dato il circuito in figura:
a
1
2
c
3
b
T
v1 = 3V
d
v2 = 2V
v3 = 4V
4
5
e
determinare la tensione punto-punto tra i nodi b e d quando l’interruttore T è aperto.
A tale scopo enunciamo la L.K.T. relativamente ad una sequenza chiusa di nodi:
Per ogni circuito concentrato connesso, lungo una qualsiasi sequenza chiusa di nodi, in ogni
istante t, la somma delle tensioni punto-punto (prese nello stesso ordine della sequenza di nodi) è
uguale a zero
Impostiamo allora la L.K.T. alla sequenza chiusa di nodi a-b-d-c-a:
v ab + vbd + v dc + v ca = 0
A questo punto esprimiamo le tensioni punto punto in funzione delle tensioni di lato note:
v ab = v1
v dc = −v3
vca = −v 2
e sostituiamo il tutto all’interno dell’equazione di equilibrio:
vbd = −v ab − v dc − vca = −v1 + v3 + v 2 = −3 + 2 + 4 = 3V
Esercizio n°7
Dato il bipolo in figura:
i(t)
v(t)
in cui abbiamo fissato la convenzione dell’utilizzatore, calcolare la potenza istantanea
assorbita nei seguenti casi:
1) v(t ) = 2V
i (t ) = 2 A
2) v(t ) = 2V
i (t ) = −3 A
3) v(t ) = −9V
i (t ) = 1A
Si ha:
1) p (t ) = v(t ) ⋅ i (t ) = 2V ⋅ 2 A = 4W > 0
⇒
potenza assorbita
2) p (t ) = v(t ) ⋅ i (t ) = 2V ⋅ (−3 A) = −6W < 0 ⇒
potenza erogata
3) p(t ) = v(t ) ⋅ i (t ) = −9V ⋅ 1A = −9W > 0
potenza erogata
⇒
Esercizio n°8
Dato il circuito in figura:
1 iA
2
A
iB
vB = 2V
vC = 5V
D
B
vE = 9/8V
iA = 8A
E
3
C
iB = 1A
4
determinare la potenza assorbita da ciascun elemento e verificare la conservazione della
potenza.
La somma algebrica delle potenze assorbite da tutti gli elementi di un circuito è nulla in ogni
istante.
In primo luogo determiniamo le tensioni ai capi dei bipoli A e D scrivendo le LKT alle
maglie DBC e ADE poi. A tale scopo fissiamo delle polarità di riferimento per le tensioni
incognite e dei versi di percorrenza delle maglie:
1
iA +
-
2
A
iB
vB = 2V
vC = 5V
+
_
D
B
vE = 9/8V
iA = 8A
E
3
C
iB = 1A
4
maglia DCB:
v B − vC − v D = 0
⇒
v D = v B − vC = 2 − 5 = −3V
maglia ADE:
v A + vD + vE = 0
⇒
v A = −v D − v E = 3 −
9 15
= V
8 8
A questo punto determiniamo le correnti nei rami del circuito in cui non sono note, avendo
fissato arbitrariamente dei versi di riferimento:
1
iA +
-
2
A
nodo 1:
iE = i A = 8 A
nodo 2:
i A = iD + iB
nodo 4:
iC = i B = 1 A
vB = 2V
iD
+
_
E
iB
vC = 5V
D
iE
3
⇒
B
C
vE = 9/8V
iA = 8A
iC
4
iB = 1A
iD = i A − iB = 8 − 1 = 7 A
Note le correnti e le tensioni ai capi di ciascun elemento, possiamo valutare la potenza
assorbita da ciascuno di essi:
⇒
assorbita
elemento B (convenzione utilizzatore):
15
⋅ 8 = 15W > 0
8
p B = v B ⋅ i B = 2 ⋅ 1 = 2W > 0
⇒
assorbita
elemento C (convenzione generatore):
pC = vC ⋅ i B = 5 ⋅ 1 = 5W > 0
⇒
erogata
elemento D (convenzione utilizzatore):
p D = v D ⋅ i D = −3 ⋅ 7 = −21W < 0
⇒
erogata
elemento E (convenzione utilizzatore):
pE = vE ⋅ i A =
⇒
assorbita
elemento A (convenzione utilizzatore):
pA = vA ⋅ iA =
9
⋅ 8 = 9W > 0
8
A questo punto per verificare la conservazione della potenza sommiamo tutte le potenze
calcolate. A tale scopo assicuriamoci che per ogni elemento sia stata adottata la stessa
convenzione. Notiamo che per tutti gli elementi è stata fissata la convenzione
dell’utilizzatore eccetto che per l’elemento C, per il quale è stata fissata quella del
generatore. E’ necessario allora riportare la potenza calcolata per questo elemento alla
convenzione dell’utilizzatore e per far ciò bisogna cambiare il segno della potenza pC (con
la convenzione dell’utilizzatore una potenza erogata è negativa).
A questo punto si ha:
p A + p B + pC + p D + p E = 15 + 2 − 5 − 21 + 9 = 0
In alternativa possiamo verificare l’equilibrio tra potenza assorbita e potenza erogata, a
prescindere dai segni e dalle convenzioni:
p assorbita = 15 + 2 + 9 = 26W
p erogata = 15 + 21 = 26W
Poniamo in forma vettoriale le tensioni e le correnti del circuito che soddisfano le L.K.:
v = (v A , v B , v C , v D , v E ) T
⇒
vettore delle tensioni che soddisfano la LKT
i = (i A , i B , iC , i D , i E ) T
⇒
vettore delle correnti che soddisfano la LKC
Sostituiamo i valori:
15
9
v = ( ,2,−5,−3, )
8
8
i = (8,1,1,7,8)
in cui per l’elemento C abbiamo scambiato la polarità della tensione, e quindi abbiamo
invertito il segno, per riportarlo alla convenzione dell’utilizzatore (avremmo potuto in
alternativa invertire il verso della corrente iC).
Se moltiplichiamo scalarmente i due vettori otteniamo:
v × i = ∑ vi ii = 15 + 2 − 5 − 21 + 9 = 0
i
e questo risultato corrisponde alla conservazione della potenza verificata sopra.
Esercizio n°9
Dato il circuito in figura:
1
A
iE
vA = 1V
vC = 4V
E
D
2
iA
B
vD = 1V
pB = 4W
C
3
iC
iC = 4A
4
calcolare la tensione vE e la corrente iE e verificare la conservazione della potenza.
Calcoliamo la tensione vE scrivendo la LKT alla maglia CDE:
maglia CDE:
v D + v E − vC = 0
⇒
v E = vC − v D = 4 − 1 = 3V
Calcoliamo la corrente iE scrivendo la LKC al nodo 4:
nodo 4:
iC = i A + i E =
pB
+ iE
vB
⇒
iE = −
pB
+ iC
vB
Calcoliamo la tensione vB scrivendo la LKT alla maglia ABE:
maglia ABE:
⇒
v A + vB − vE = 0
v B = v E − v A = 3 − 1 = 2V
A questo punto possiamo calcolare il valore di iE :
iE = −
pB
4
+ iC = − + 4 = 2 A
vB
2
mentre è evidentemente:
iA =
pB 4
= = 2A
vB 2
Note le correnti e le tensioni ai capi di ciascun elemento, possiamo valutare la potenza
assorbita da ciascuno di essi:
elemento A (convenzione utilizzatore):
p A = v A ⋅ i A = 1 ⋅ 2 = 2W > 0
⇒
assorbita
elemento B (convenzione utilizzatore):
p B = v B ⋅ i A = 2 ⋅ 2 = 4W > 0
⇒
assorbita
elemento C (convenzione generatore):
pC = vC ⋅ iC = 4 ⋅ 4 = 16W > 0
⇒
erogata
elemento D (convenzione utilizzatore):
p D = v D ⋅ iC = 1 ⋅ 4 = 4W > 0
⇒
assorbita
elemento E (convenzione utilizzatore):
p E = v E ⋅ i E = 3 ⋅ 2 = 6W > 0
⇒
assorbita
Riportiamo la potenza dell’elemento C alla convenzione dell’utilizzatore (cambiando
semplicemente il segno) e sommiamo i contributi dei diversi elementi:
p A + p B + pC + p D + p E = 2 + 4 − 16 + 4 + 6 = 0
verificando così la conservazione della potenza.
Esercizio n°10
La corrente e la tensione in un bipolo variano nel tempo come indicato in figura:
v [V]
30
5
0
10 15
25
0
10 15
25
t(s)
i [A]
30
t(s)
Tracciare la potenza fornita al bipolo per t > 0. Qual è l’energia totale fornita al bipolo tra
t=0s e t=25s? Il bipolo utilizza la convenzione degli utilizzatori.
La potenza istantanea p(t) è definita come il prodotto dei valori delle tensione e della
corrente all’istante t:
p (t ) = v(t )i (t )
In primo luogo determiniamo le espressioni analitiche delle diverse rette che costituiscono
l’andamento di v e di i:
v(t ) = 30
i (t ) = 2t
⇒ p (t ) = 60t
10 ≤ t ≤ 15 ⇒
v(t ) = −5t + 80
i (t ) = 2t
⇒ p(t ) = −10t 2 + 160t
15 ≤ t ≤ 25 ⇒
v(t ) = 5
i (t ) = −3t + 75
⇒
0 ≤ t ≤ 10
⇒
p (t ) = −15t + 375
Calcoliamo i valori della potenza agli estremi di ciascun intervallo di tempo:
p (0) = 0W
p(15) = −10 ⋅ (15) 2 + 160 ⋅ 15 = 150W
p(10) = 600W
p(25) = −15 ⋅ 25 + 375 = 0W
A questo punto possiamo determinare l’andamento della potenza in tutto l’intervallo [0;25]:
p(t)
t
L’energia scambiata da un bipolo in un intervallo di osservazione (t 0 , t1 ) vale:
w(t0 , t1 ) = ∫ p(t )dt = ∫ v(t ) ⋅ i (t )dt
t1
t1
t0
t0
Nel nostro caso abbiamo quindi:
w(0,25) = ∫ 0 p (t )dt = ∫ 0 p(t )dt + ∫ 10 p(t )dt + ∫ 15 p (t )dt
25
10
15
25
da cui:
w(0,25) = ∫ 0 60tdt + ∫ 10 (−10t 2 + 160t ) dt + ∫ 15 (−15t + 375)dt
10
15
25
w(0,25) = 60∫ 0 tdt − 10 ∫ 10 t 2 dt + 160 ∫ 10 tdt − 15∫ 15 tdt + 375∫ 15 dt
10
15
10
15
15
25
15
25
25
⎡t 2 ⎤
⎡t 3 ⎤
⎡t 2 ⎤
⎡t 2 ⎤
25
w(0,25) = 60⎢ ⎥ − 10 ⎢ ⎥ + 160⎢ ⎥ − 15⎢ ⎥ + 375[t ]15
⎣ 2 ⎦0
⎣ 3 ⎦ 10
⎣ 2 ⎦ 10
⎣ 2 ⎦ 15
In definitiva:
⎡ (10) 2 ⎤
⎡ (15) 3 (10) 3 ⎤
⎡ (15) 2 (10) 2 ⎤
⎡ (25) 2 (15) 2 ⎤
w(0,25) = 60 ⎢
−
−
−
⎥ − 10 ⎢
⎥ + 160 ⎢
⎥ − 15⎢
⎥ + 375[25 − 15]
3 ⎦
2 ⎦
2 ⎦
⎣ 2 ⎦
⎣ 3
⎣ 2
⎣ 2
⎡ (3375) − 1000 ⎤
⎡ 225 − 100 ⎤
⎡ 625 − 225 ⎤
w(0,25) = 3000 − 10⎢
+ 160 ⎢
− 15⎢
⎥
⎥
⎥⎦ + 3750
3
2
2
⎣
⎦
⎣
⎦
⎣
⎡125 ⎤
⎡ 2375 ⎤
− 15[200] + 3750
+ 160⎢
w(0,25) = 3000 − 10⎢
⎥
⎣ 2 ⎥⎦
⎣ 3 ⎦
⎡ 2375 ⎤
+ 80[125] − 15[200] + 3750
w(0,25) = 3000 − 10⎢
⎣ 3 ⎥⎦
⎡ 2375 ⎤
⎡ 2375 ⎤
= 5833.3J
+ 10000 − 3000 + 3750 = 13750 − 10 ⎢
w(0,25) = 3000 − 10⎢
⎥
⎣ 3 ⎥⎦
⎣ 3 ⎦
Tale energia è pari all’area sottesa dalla curva della potenza sull’asse dei tempi. Poiché
stiamo adottando la convenzione dell’utilizzatore possiamo dire che in ogni istante di
tempo t ∈ [0;25] il nostro componente sta assorbendo potenza perché è sempre:
p(t ) ≥ 0
L’energia complessivamente assorbita vale allora 5833 J.
Esercizio n°11
Un bipolo è collegato ad un generatore di corrente i avente la seguente forma d’onda:
i [A]
1
i
+
v
-
0
1
2
t(s)
0
1
2
t(s)
v [V]
3
La corrispondente tensione ha la forma d’onda indicata sopra. Determinare la potenza p(t)
e l’energia w(t) assorbita dal bipolo. Tracciare il grafico di p(t) e w(t).
In primo luogo determiniamo le espressioni analitiche delle diverse rette che costituiscono
l’andamento di v e di i:
0 ≤ t ≤ 0 .5
⇒
v(t ) = 6t
i (t ) = 1
⇒ p (t ) = 6t
0 .5 ≤ t ≤ 1
⇒
v(t ) = −6t + 6
i (t ) = 1
⇒ p (t ) = −6t + 6
1≤ t ≤ 2
⇒
v(t ) = 0
i (t ) = −t + 2
⇒ p(t ) = 0
L’andamento della potenza istantanea è allora dato da:
p [W]
3
0
1
2
t(s)
ed è identico a quello della tensione.
Calcoliamo l’andamento dell’energia w(t) a partire da quello della potenza istantanea,
essendo:
p(t ) =
dw(t )
dt
t
w(t ) = ∫ p(τ )dτ
⇒
−∞
Se supponiamo che la potenza è nulla fino all’istante 0 possiamo scrivere:
0
t
−∞
0
= ∫ 0dτ + ∫ 6τdτ
w(t )
0 ≤ t ≤ 0 .5
0
0.5
t
−∞
0
0.5
0
0.5
1
t
−∞
0
0.5
1
= ∫ 0dτ + ∫ 6τdτ + ∫ (−6τ + 6)dτ
0 .5 ≤ t ≤ 1
= ∫ 0dτ + ∫ 6τdτ + ∫ (−6τ + 6)dτ + ∫ 0dτ
1≤ t ≤ 2
Si ha quindi:
= 3t 2
w(t )
0 ≤ t ≤ 0 .5
t
t
0.5
0.5
1
1
0.5
0.5
= [3t 2 ]00.5 − ∫ 6τdτ + ∫ 6dτ
= [3t 2 ]00.5 − ∫ 6τdτ + ∫ 6dτ + 0
= 3t 2
w(t )
0 .5 ≤ t ≤ 1
1≤ t ≤ 2
0 ≤ t ≤ 0 .5
=
3
− [3t 2 ]t0.5 + 6t − 3
4
0 .5 ≤ t ≤ 1
=
3
− [3t 2 ]10.5 + 6(1 − 0.5)
4
1≤ t ≤ 2
In definitiva:
= 3t 2
w(t )
0 ≤ t ≤ 0 .5
=
3
3
− [3t 2 − ] + 6t − 3
4
4
0 .5 ≤ t ≤ 1
=
3
3
− [3 − ] + 6(1 − 0.5)
4
4
1≤ t ≤ 2
In definitiva:
= 3t 2
w(t )
0 ≤ t ≤ 0 .5
= −3t 2 + 6t −
=
3
2
0 .5 ≤ t ≤ 1
3
3
3
−3+ + 6−3 =
4
4
2
1≤ t ≤ 2
Calcoliamo i valori dell’energia agli estremi di ciascun intervallo di tempo considerato:
w(0) = 0 J
w(0.5) = 0.75 J
w(1) = 1.5
A questo punto possiamo determinare l’andamento dell’energia nell’intervallo [0;2]: