NOME ...................................................
DATA ...............
CLASSE .............
CONGRUENZA DEI TRIANGOLI
Con riferimento alle figure e alle ipotesi indicate, dimostrare la tesi di ciascuno dei seguenti esercizi.
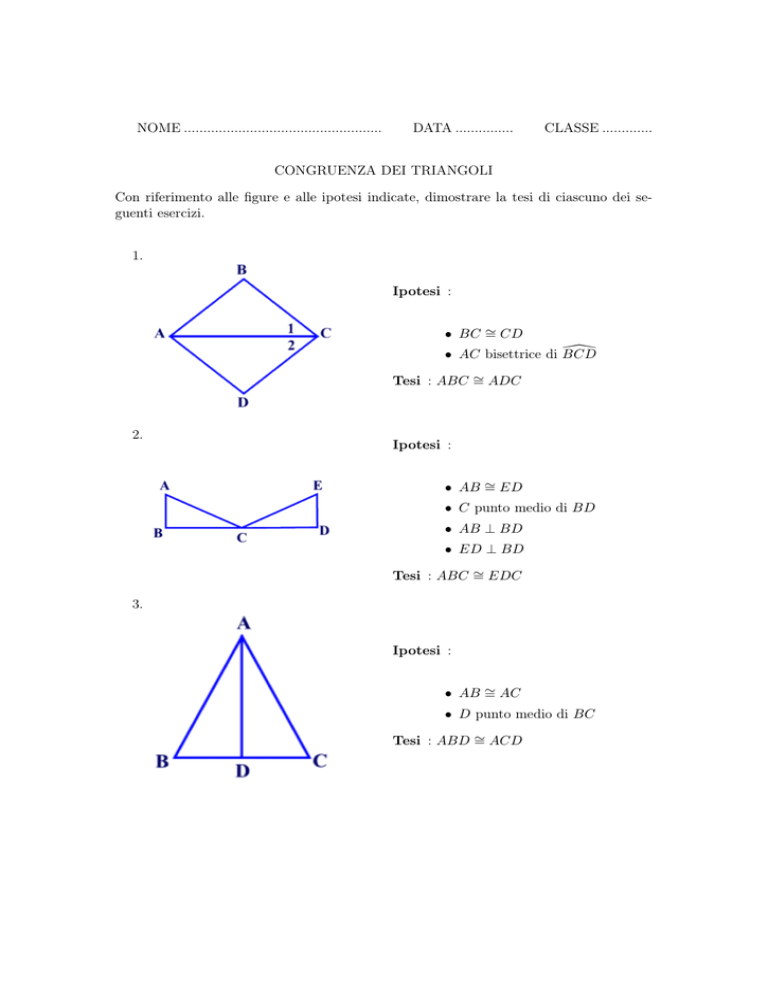
1.
Ipotesi :
• BC ∼
= CD
\
• AC bisettrice di BCD
Tesi : ABC ∼
= ADC
2.
Ipotesi :
• AB ∼
= ED
• C punto medio di BD
• AB ⊥ BD
• ED ⊥ BD
Tesi : ABC ∼
= EDC
3.
Ipotesi :
• AB ∼
= AC
• D punto medio di BC
Tesi : ABD ∼
= ACD
4.
Ipotesi :
• AC ∼
= EF
∼
b
b
• A=E
• AC ⊥ BD
• EF ⊥ BD
b∼
b
Tesi : B
=D
5.
Ipotesi :
• AD ∼
= CD
∼
• b
3=b
4
\
Tesi : DB bisettrice di ABC
6.
Ipotesi :
• AB ∼
= EB
∼
b
b
• A=E
Tesi : AD ∼
= EC
7.
Ipotesi :
• AE ∼
= AC
\∼
\
• CAB
= DAE
• A punto medio di BD
Tesi : BEA ∼
= DCA
8.
Ipotesi :
• b
4∼
6
=b
∼b
• b
1=
3
• b
4∼
5
=b
b∼
Tesi : R
= Tb
9.
Ipotesi :
• b
1∼
2
=b
∼b
• b
7=
8
Tesi : b
5∼
6
=b
10.
Ipotesi :
• CE ∼
= BF
• AB ∼
= ED
\∼
\
• CBA
ED
=F
• AC ⊥ BA
• ED ⊥ F D
Tesi : ABC ∼
= DEF
SOLUZIONI
1.
ASSERZIONE
(a) BC ∼
= CD
∼
b
b
(b) 1 = 2
(c) AC ∼
= AC
(d) ABC ∼
= ADC
MOTIVAZIONE
per ipotesi
la bisettrice AC divide l’angolo in parti congruenti
per la proprietà riflessiva della
congruenza
per LAL
L asserzione (a)
A asserzione (b)
L asserzione (c)
2.
ASSERZIONE
(a) AB ∼
= ED
∼
b
b
(b) B = D
(c) BC ∼
= DC
(d) ABC ∼
= EDC
MOTIVAZIONE
per ipotesi
perché angoli entrambi retti formati da rette tra loro
perpendicolari
perché il punto medio C
divide a metà il segmento BD
per LAL
L asserzione (a)
A asserzione (b)
L asserzione (c)
3.
ASSERZIONE
(a) AB ∼
= AC
(b) BD ∼
= DC
(c) AD ∼
= AD
(d) ABD ∼
= ACD
MOTIVAZIONE
per ipotesi
perché D è il punto medio di
BC
per la proprietà riflessiva della
congruenza
per LLL
L asserzione (a)
L asserzione (b)
L asserzione (c)
4.
ASSERZIONE
b∼
b
(a) A
=E
∼
(b) AC = EF
(c) b
1∼
2
=b
(d) ABC ∼
= EDF
MOTIVAZIONE
per ipotesi
per ipotesi
perché angoli entrambi retti formati da rette tra loro
perpendicolari
per ALA
A asserzione (a)
L asserzione (b)
A asserzione (c)
b∼
b
(e) B
=D
perché parti corrispondenti di
triangoli congruenti
5.
ASSERZIONE
(a) AD ∼
= CD
b
(b) b
1∼
=2
(c) BD ∼
= BD
(d) ABD ∼
= CBD
MOTIVAZIONE
per ipotesi
perché angoli supplementari
di angoli tra loro congruenti
(b
1+b
3=π eb
2+b
4 = π)
per la proprietà riflessiva
per LAL
L asserzione (a)
A asserzione (b)
L asserzione (c)
(e) b
5∼
6
=b
\
(f) DB bisettrice di ABC
perché parti corrispondenti di
triangoli congruenti
perché la bisettrice divide
l’angolo in parti congruenti
6.
ASSERZIONE
b∼
b
(a) A
=E
(b) AB ∼
= BE
b
b∼
(c) B
=B
(d) ABC ∼
= EBD
MOTIVAZIONE
per ipotesi
per ipotesi
per la proprietà riflessiva
per ALA
A asserzione (a)
L asserzione (b)
A asserzione (c)
(e) BD ∼
= BC
(f) AD ∼
= CE
perché parti corrispondenti di
triangoli congruenti
per la proprietà transitiva:
AD ∼
= AB − BD ∼
= BE −
∼
BC = CE
7.
ASSERZIONE
(a) AE ∼
= AC
(b) b
1∼
3
=b
(c) AB ∼
= AD
(d) BEA ∼
= DCA
MOTIVAZIONE
per ipotesi
per la proprietà transitiva:
\−b
\ −b
b
1∼
2∼
2∼
3
= BAC
= DAE
=b
perché A punto medio di BD
per LAL
L asserzione (a)
A asserzione (b)
L asserzione (c)
8.
ASSERZIONE
\
[
(a) P
QR ∼
= SQT
(b) P Q ∼
= QS
(c) b
4∼
5
=b
(d) P QR ∼
= SQT
MOTIVAZIONE
per la proprietà transitiva:
\
[
P
QR ∼
1+b
2∼
3+b
2∼
=b
=b
= SQT
perché lati obliqui del triangolo isoscele P QS con angoli alla
base b
4∼
6
=b
per ipotesi
per ALA
A asserzione (a)
L asserzione (b)
A asserzione (c)
b∼
(e) R
= Tb
perché parti corrispondenti di
triangoli congruenti
9.
ASSERZIONE
(a) b
3∼
4
=b
(b) BE ∼
= BE
∼
b
b
(c) 7 = 8
(d) ABE ∼
= CBE
MOTIVAZIONE
perché angoli supplementari
di angoli tra loro congruenti
(b
1+b
3=π eb
2+b
4 = π)
per la proprietà riflessiva
per ipotesi
per ALA
A asserzione (a)
L asserzione (b)
A asserzione (c)
(e) AE ∼
= CE
(f) b
5∼
6
=b
perché parti corrispondenti di
triangoli congruenti
perché angoli alla base del
triangolo isoscele AEC con
lati obliqui AE ∼
= CE
10.
ASSERZIONE
b∼
b
(a) A
=D
(b) AB ∼
= ED
\∼
\
(c) CBA
ED
=F
∼
(d) ABC = DEF
MOTIVAZIONE
perché angoli entrambi retti formati da rette tra loro
perpendicolari
per ipotesi
per ipotesi
per ALA
A asserzione (a)
L asserzione (b)
A asserzione (c)











