1°Legge di Kirchoff (ai nodi):
. La somma delle correnti entranti in un nodo deve essere pari a 0;
qualunque sia il regime la carica racchiusa in un nodo è pari a 0.
2°Legge di Kirchoff (alle maglie):
. La somma delle tensioni lungo un percorso chiuso deve essere pari a 0.
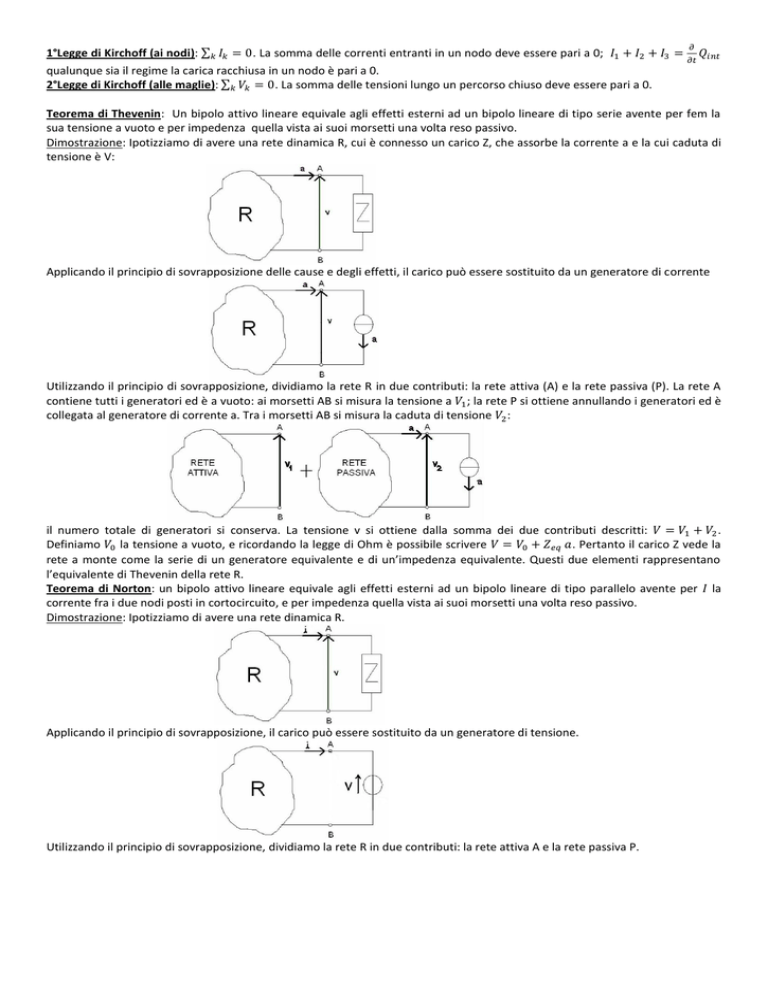
Teorema di Thevenin: Un bipolo attivo lineare equivale agli effetti esterni ad un bipolo lineare di tipo serie avente per fem la
sua tensione a vuoto e per impedenza quella vista ai suoi morsetti una volta reso passivo.
Dimostrazione: Ipotizziamo di avere una rete dinamica R, cui è connesso un carico Z, che assorbe la corrente a e la cui caduta di
tensione è V:
Applicando il principio di sovrapposizione delle cause e degli effetti, il carico può essere sostituito da un generatore di corrente
Utilizzando il principio di sovrapposizione, dividiamo la rete R in due contributi: la rete attiva (A) e la rete passiva (P). La rete A
contiene tutti i generatori ed è a vuoto: ai morsetti AB si misura la tensione a ; la rete P si ottiene annullando i generatori ed è
collegata al generatore di corrente a. Tra i morsetti AB si misura la caduta di tensione :
il numero totale di generatori si conserva. La tensione v si ottiene dalla somma dei due contributi descritti:
.
Definiamo
la tensione a vuoto, e ricordando la legge di Ohm è possibile scrivere
. Pertanto il carico Z vede la
rete a monte come la serie di un generatore equivalente e di un’impedenza equivalente. Questi due elementi rappresentano
l’equivalente di Thevenin della rete R.
Teorema di Norton: un bipolo attivo lineare equivale agli effetti esterni ad un bipolo lineare di tipo parallelo avente per la
corrente fra i due nodi posti in cortocircuito, e per impedenza quella vista ai suoi morsetti una volta reso passivo.
Dimostrazione: Ipotizziamo di avere una rete dinamica R.
Applicando il principio di sovrapposizione, il carico può essere sostituito da un generatore di tensione.
Utilizzando il principio di sovrapposizione, dividiamo la rete R in due contributi: la rete attiva A e la rete passiva P.
E’ evidente che
. Definiamo
la corrente in cortocircuito e ricordando la legge di Ohm, è possibile scrivere
. Pertanto il carico Z vede la rete a monte come il parallelo di un generatore equivalente e di un’impedenza
equivalente. Questi due elementi rappresentano l’equivalente di Norton della rete R.
Corollario di Millman: In una rete lineare costituita da n rami in parallelo, la tensione VAB ai capi del parallelo è data da:
Principio di sovrapposizione delle cause e degli effetti: La risposta di una rete lineare alla sollecitazione di più generatori
indipendenti può essere ottenuta considerando ciascun generatore separatamente attivo e sommando le rispettive risposte di
rete:
Analisi ai nodi: [A]=matrice incidenza:
Analisi agli anelli:
Condensatore a facce piane parallele:
Nel condensatore vi è un fenomeno di dispersione della corrente elettrica, perché anche l’aria polarizza. Tuttavia, ammettiamo
che la distanza d sia così modesta che il contributo dell’aria sia trascurabile. Allora vale:
;
In seguito, pongo tra le due facce un materiale:
aumenta il contributo del vuoto.
Energia accumulata nel condensatore:
dove
indica di quante volte il contributo dielettrico
. Ora posso calcolare l’energia accumulata per unità di volume:
Equazione di Ohm nel dominio fasoriale: Legge di Ohm:
Heaveside:
ricaviamo:
anche in alternata, ponendo:
. Dalla definizione di operatore di
. Per il teorema di Kennelly-Steinmetz ogni legge in corrente continua vale
e
. Otteniamo quindi:
Teorema di Kennelly-Steinmetz: Qualunque problema relativo alle correnti sinusoidali si può risolvere assumendo la formula
risolutiva dello stesso problema per correnti continue e sostituendo i simboli complessi di correnti e tensioni ai simboli reali, le
impedenze e le ammettenze (complesse) dei singoli elementi alle resistenze e alle conduttanze.
Energia immagazzinata nell’induttore:
, dove i è la corrente che scorre nell’induttore e L l’induttanza. L’energia immagazzinata nell’induttore è
uguale alla quantità di lavoro richiesta per ottenere la corrente che scorre in esso, e quindi, per generare il campo magnetico.
Amplificatore operazionale: si compone di due morsetti di ingresso, un morsetto di uscita e due morsetti di alimentazione.
L’alimentazione è necessaria per poter erogare la potenza richiesta in uscita, quindi la tensione di uscita rimarrà sempre
compresa tra due valori, cioè quelli di alimentazione. La massima e minima tensione di uscita, funzione della tensione di
ingresso, prendono il nome di tensione di saturazione. Costruzione del circuito equivalente: in un amplificatore operazionale
reale si identificano le seguenti grandezze: corrente i+ e i- assorbite dai terminali invertenti e non invertenti; la differenza di
potenziale tra il morsetto non invertente e quello invertente, definita “tensione di ingresso differenziale”
; la
tensione di uscita, dipende dalla differenza di potenziale tra i morsetti di ingresso e della tensione di alimentazione e può essere
approssimata:
in “zona lineare”,
in “zona saturazione”. L’elemento ideale ha queste
caratteristiche: correnti i+ e i- pari a 0; guadagno in anello aperto (=A) infinito. Quest’ultima condizione implica che la tensione di
uscita possa variare nell’intervallo
solo nel caso in cui si realizzi la condizione sugli ingressi di “corto circuito virtuale”,
ovvero che i morsetti siano allo stesso potenziale. Quindi la tensione di uscita può assumere un qualunque valore compreso tra
in presenza di tensione differenziale nulla; se la tensione differenziale è positiva, la tensione di uscita si porta al valore di
; se la tensione differenziale è negativa, la tensione di uscita si porta al valore di
.
Funzionamento in anello aperto: si verifica quando il valore dell’uscita non viene riportato dai circuiti di retroazione su uno dei
morsetti di ingresso. In questo caso, il comportamento è di tipo “amplificatore differenziale”, esso si porterà a lavorare in zona di
saturazione a seconda dei livelli di tensione a cui si portano gli ingressi.
Funzionamento in anello chiuso: il valore dell’uscita è riportato da circuiti di retroazione su uno dei morsetti di ingresso. In
questo caso, cerca di adeguare la tensione di uscita in modo da realizzare la condizione di corto circuito virtuale. Se la tensione
di uscita è fra
, allora lavorerà in zona lineare, altrimenti in zona di saturazione.
Comparatore o rilevatore di soglia:
Se il valore della tensione applicato è superiore al valore della tensione di riferimento, allora l’amplificatore va in saturazione
positiva; se è minore va in saturazione negativa:
Nelle applicazioni si verifica che il valore di riferimento è costituito da un valore di tensione costante in questo caso si parla di
“rilevatore di soglia”, se il terminale invertente è collocato al potenziale di riferimento il rilevatore si chiama “rilevatore di zero”.
Amplificatore invertente: il circuito è retro azionato attraverso , allora l’amplificatore lavora in zona lineare (solo se c’è un
corto circuito virtuale si ha
e una
compresa tra
).
Dall’analisi della maglia di ingresso:
; dall’equilibrio alla maglia con
circolante è quindi data da:
. Dall’analisi alle correnti al nodo A si ha:
. La tensione di uscita è quindi amplificata da un fattore
:
la corrente
detto guadagno dell’amplificatore e cambiata di segno
(caratteristica contenuta nel termine “invertente”).
Sommatore invertente: esso non è altro che la formulazione a più ingressi dell’amplificatore invertente. Si ipotizzi che funzioni
in zona lineare. Dalla relazione di equilibrio delle correnti al nodo comune si ha:
. Per l’ipotesi di
funzionamento in zona lineare si ha:
. Questo circuito opera dunque
una somma pesata dei segnali di ingresso; per avere un sommatore puto (tutti i segnali di ingresso vengono sommati con lo
stesso peso) è necessario che tutte le resistenze in serie alle sorgenti di tensione abbiano il medesimo valore; da queste
resistenze ho:
.
Amplificatore non invertente: circuito retro azionato tramite
si ritiene che l’amplificatore lavori in zona lineare, che
e
che si realizzi con una tensione di uscita
compresa tra
. Dall’analisi alla maglia costituita da
e
si ha:
;
per l’equilibrio al nodo A si ha:
. La maglia costituita da
può essere vista come un partitore di tensione
resistivo alimentato da una sorgente di tensione di valore pari a
. Allora
è data da:
. Il guadagno può assumere solo valori positivi e maggiori di 1 solo nel caso in cui nel ramo di
retroazione ci sia un cortocircuito (
). In questo caso il circuito è “inseguitore di tensione” in quanto
e svolge la
funzione di adattatore di impedenza.
Integratore invertente: la tipologia è simile a quella dell’amplificatore invertente, l’unica differenza è l’elemento sul circuito di
retroazione. Si ipotizzi che funzioni in zona lineare. Dall’analisi alla maglia di ingresso si ha:
costituita da
:
; l’equilibrio alla maglia
; la corrente in questa maglia è:
correnti al nodo si ha:
. Posto
; dall’analisi delle
si ha la caratteristica di trasferimento:
; nel caso in cui il segnale di ingresso è periodico si ha:
.
Questo circuito presenta problemi con segnali a bassa frequenza, a causa dell’elevato valore di guadagno; l’ampiezza del segnale
di uscita può portare l’amplificatore operazionale in saturazione. Per evitare ciò basta inserire una resistenza
in parallelo alla
capacità: così si trasforma l’integratore puro in un filtro passa basso del 1° ordine. Con frequenze minori a quella di taglio
(
) il comportamento del circuito è di tipo amplificatore invertente, mentre per frequenze superiori il comportamento è
di tipo integratore.
Teorema di Ferraris: Consideriamo 3 bobine percorse da corrente, sfasate di
rappresentare spazialmente:
ricavare in modo univoco
una bobina (considerando
otteniamo
, definendo
. Definiamo uno spazio vettoriale per
otteniamo
. Si possono
. Analizzando il campo magnetico del traferro di
. Facendo la serie di Fourier al primo termine
) otteniamo un campo magnetico
. Scriviamo un fasore spaziale anche per il campo magnetico:
. Consideriamo le 3 correnti simmetriche ed equilibrate (sfasate temporalmente di
e dello stesso valor medio):
,
,
, si ottiene
quindi
un fasore rotante di pulsazione
temporalmente e spazialmente di
Conduttanza:
e ampiezza
ma
cioè
. Da 3 bobine fisse ma attraversate da corrente alternata, sfasate
abbiamo ottenuto un campo magnetico rotante nello spazio.











