Classe I SEZ. E
Prof.ssa Verena Libardi
COMPITI PER LE
VACANZE ESTIVE 2014
Consolidamento –
SCIENZE
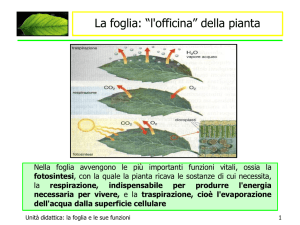
IMPARIAMO A GUARDARE UNA FOGLIA
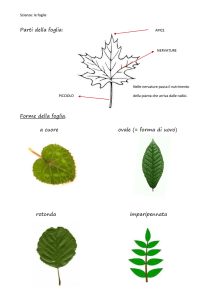
In una foglia possiamo distinguere la
lamina (1), che è la parte più larga che le
consente di “catturare” la luce solare ed
il picciolo (2), che fa da collegamento
con il resto della pianta. Il picciolo, nel
punto in cui si inserisce sul ramo si dilata
brevemente, un poco ad abbracciarlo,
questa parte si chiama guaina (3).
Alcune foglie hanno un picciolo molto
breve o del tutto mancante, in questo
caso si dicono foglie sessili. In alcune
specie, alla base del picciolo compaiono
due piccole foglioline accessorie, le
stipole (4).
Una parte importante della foglia sono le nervature (5), si tratta di una rete di
tubicini che raggiungono la foglia attraverso il picciolo e poi si diramano a tutta la
lamina; alcuni servono per fornire alle cellule l’acqua che la pianta assorbe dal
terreno tramite le radici, mentre altri hanno la funzione inversa, raccogliere le
sostanze elaborate dalla lamina fogliare per distribuirle a tutta la pianta.
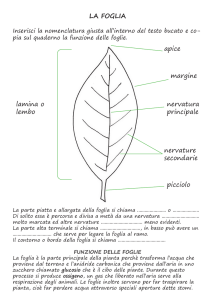
Per descrivere una foglia
dobbiamo anzitutto far caso si si
tratta di una foglia semplice (a),
formata da una lamina unica,
anche se lobata (b) o frastagliata,
oppure se è suddivisa in tante
foglioline più piccole, cioè e una
foglia composta.
In quest’ultimo caso ci sono due possibilità: le foglioline si distribuiscono lungo il
picciolo (foglia pennata) (c) o partono tutte da uno stesso punto (foglia palmata)
(d).
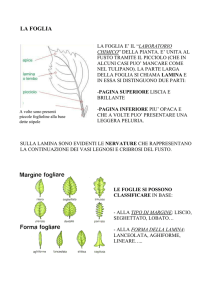
Le forme che può assumere
la lamina di una foglia sono
innumerevoli, nella figura
sono illustrate le più
frequenti; si va dalla forma
ad ago (si dice foglia
aghiforme) (e) tipica dei
pini, degli abeti e di altre conifere, a quella a nastro (foglia lineare) (f) dei cosiddetti
fili d’erba e di molte piante coltivate per i loro fiori (tulipani, giacinti, crochi, ecc.
).Una forma stretta ed allungata si definisce lanceolata (g), poi possiamo trovare
quella ovale o ellittica (h).
Una abbastanza frequente è
quella con un profilo analogo, ma
con la parte più larga spostata
verso l’apice (foglia obovata) (i).
Vi sono poi foglie rotondeggianti
(l), triangolari (m), a cuore e via
dicendo.
Uno sguardo particolare merita il
margine. Può essere liscio (n),
ma più spesso si presenta con
tanti dentelli; se questi hanno
una punta arrotondata il margine
si definisce crenato (o), se sono
più o meno irregolari ed
appuntiti si dice dentato (p), se i
dentelli sono regolari e orientati
in avanti, come i denti di una
sega, si dice appunto seghettato
(q).
È
importante
anche
osservare la distribuzione delle
nervature.
Possono avere un andamento parallelo (foglia parallelinervia) (r), vi può essere una
nervatura principale da cui se ne diramano altre sia a destra che a sinistra (foglia
penninervia) (s) oppure vi possono essere più nervature importanti che partono dal
picciolo e ciascuna poi si dirama in direzione diversa (foglia palminervia) (t).
ATTIVITÀ PRATICA
Raccogli qualche foglia in campagna, in un parco o in un giardino e prova a farne una
descrizione scritta, seguendo lo schema che trovi qui sotto.
1)
2)
3)
4)
5)
6)
7)
8)
9)
La foglia è semplice o composta?
Se è composta, è di tipo pennato o palmato?
Se è semplice, è intera o suddivisa in lobi più o meno profondi?
C’è il picciolo? Quanto è lungo? O si tratta di una foglia sessile?
Quanto è lunga l’intera foglia? Quanto è larga? (esprimi la misura in
millimetri)
Com’è la forma complessiva della lamina? Cerca i termini che ti sembrano più
appropriato nella figura; puoi facilmente trovare delle forme intermedie (fra
ovale e lanceolata; rotondeggiante, ma con lobi pronunciati; ecc.). Puoi
sempre provare a descriverla con parole tue.
Come è il marine? (Anche in questo caso sono frequenti i casi intermedi)
Di che tipo è la nervatura?
Se lo sai scrivi anche il nome dell’albero e della pianta da cui proviene.
CONSEGNE:
• Esegui gli esercizi su un quaderno o su dei fogli a quadretti: in ogni caso
ricorda di eseguirli con cura e ordine
• Tutti gli esercizi vanno consegnati all’insegnante i primi giorni di scuola
• Se necessario, prima di svolgere gli esercizi, rivedi l’argomento sul libro o sul
quaderno
Unità 1 – Le quattro operazioni fondamentali
Risolvi le seguenti espressioni.
24 ÷ 3 − 24 ÷ 6 × 2 + 15 − 12 ÷ 2 + 18 ÷ 6 =
5 × 8 + 3 − 24 ÷ 2 − 2 × 7 − 13 + 5 × 4 =
9 × 2 − 12 ÷ 6 + 27 ÷ 9 + 5 × 4 − 2 × 8 =
18 − 3 × 3 + 1 ÷ 13 − 14 × 4 − 12 × 2 − 13 ÷ 9 =
5 + 1 + 27 ÷ 9 + 7 − 2 × 5 − 15 ÷ 3 + 5 ÷ 7 =
6 × 2 − 7 + 2 + 125 ÷ 5 − 2 × 9 × 5 − 13 × 3 − 29 ÷ 7 − 6 =
5 + 2 + 6 × 7 − 24 ÷ 4 + 3 × 9 ÷ 30 − 19 ÷ 6 =
56 ÷ 8 − 30 ÷ 10 × 64 ÷ 2 ÷ 16 + 5 × 10 − 5 ÷ 15 + 3 ÷
5 − 2 =
9. 14 ÷ 2 + 1 − 3 × 27 + 15 − 28 + 12 ÷ 8 + 4 + 20 ÷ 4 =
10.9 × 5 + 3 × 9 − 24 ÷ 2 ÷ 2 + 2 × 5 − 27 ÷ 9 × 2 + 16 ÷ 4 × 2 ÷
10 + 9 =
1.
2.
3.
4.
5.
6.
7.
8.
Unità 2 – Le potenze
Risolvi le seguenti espressioni con le potenze utilizzando, se possibile, le loro
proprietà.
23.7 × 3 + 3 × 2 × 9 − 4 + 20 × 4 + 2 ÷ 11 + 11 ÷ 6 − 5 × 4 =
24.35 ÷ 63 ÷ 3 + 18 × 6 − 4 × 2 − 3 × 2 + 17 × 2 ÷ 2 + 10 ÷
2 + 3 + 3 =
25.5 + 5 × 5 ÷ 6 ÷ 6 + 14 + 117 ÷ 38 + 3 × 7 − 4 − 2 ÷
6 =
26.2 × 2 × 3 − 3 × 2 + 3 − 2 × 3 + 5 − 3 × 2 × 3 − 7 × 2 −
15 + 2 × 3 =
27.4 ÷ 3 − 3 × 3 ÷ 3 − 2 + 2 ÷ 3 − 3 − 2 × 5 − 1 + 2 −
17 + 3 =
Unità 3 – I triangoli
Risolvi i seguenti problemi.
19.In un triangolo isoscele la base misura 27 cm e ciascun lato obliquo è i 5/3
della base. Calcola il perimetro.
20.Il perimetro di un triangolo isoscele è 43 cm e la base misura 21 cm. Calcola la
misura dei lati obliqui.
21.Un triangolo equilatero ha il lato lungo 50 cm. Calcola la misura dei due lati
obliqui di un triangolo isoscele isoperimetrico al triangolo dato e avente la
base lunga 62 cm.
22.In un triangolo un lato misura 44 cm e il perimetro è 128 cm. Sapendo che la
differenza degli altri due lati è 8 cm, calcolane la misura.
23.Un triangolo rettangolo ha l’ipotenusa lunga 147,6 cm e il perimetro di 345,6
cm. Sapendo che i due cateti sono uno il doppio dell’altro, calcolane la misura.
24.Nel triangolo ABC il lato AB misura 24 cm, il lato BC supera AB di 5 cm e il lato
AC supera BC di 3,6 cm. Calcola il perimetro del triangolo dato e quello di un
triangolo equilatero avente il lato congruente al lato AC del triangolo ABC.
Unità 4 – Le frazioni
25.Quali tra le seguenti frazioni sono equivalenti tra loro?
2 4 5 1 40 4 4 15
, , , , , , ,
3 9 8 5 60 6 20 24
26.Riduci ai minimi termini le seguenti frazioni:
28 39 200 60 92 105
, ,
, ,
,
70 65 150 84 207 60
27.Riduci le frazioni allo stesso denominatore.
a)
b)
c)
!
; ;
;
;
"
;
;
!
; ; ;
28.Vero o falso?
a) 2/8 è la frazione complementare di 6/8.
b) 2/5 è la frazione complementare di 5/5.
c) 9/10 è la frazione complementare di 10/9.
d) 4/7 è la frazione complementare di 3/4.
e) 2/3 è la frazione complementare di 1/3.
Risolvi i seguenti problemi con le frazioni.
29.Una tanica contiene 57 l di acqua. Quante bottiglie della capacità di 3/2 di
litro si possono riempire con quest’acqua?
30.Un automobilista ha percorso 120 km, che rappresentano i 3/7 del suo
viaggio. Quanti chilometri è lungo tutto il viaggio? Quanti chilometri deve
percorrere ancora?
31.Roberta vuole comperare un gioco elettronico versando un anticipo di 12 €
pari ai 2/5 del costo complessivo. Quanto costa il gioco elettronico?
32.Il segmento HK, che misura 12 cm, è 4/7 del segmento AB. Quanto misura AB?
33.Melissa grazie alle mance settimanali degli ultimi 6 mesi ha risparmiato 80 €.
Spende i 7/16 dei suoi risparmi per un regalo per la nonna. Quanti soldi le
rimangono?