Corso di Statistica (canale A – D)
Dott.ssa P. Vicard
2. Variabilità mediante il confronto di valori caratteristici della
distribuzione
Un approccio alternativo, e spesso utile, alla misura della variabilità è quello basato
sul confronto di valori caratteristici della distribuzione.
La misura più semplice è data dal campo di variazione (o range) che si indica con R.
Esso è dato dalla differenza tra la modalità più grande e la modalità più piccola.
Siano x1,…,xK le diverse modalità osservate, e supponiamo che siano ordinate in
modo crescente; allora
R = x K − x1
Quanto più piccolo è R tanto più simili e “vicine” sono le modalità osservate del
carattere. Al limite se fosse R=0, la più grande e la più piccola modalità sarebbero
uguali il che significa che tutte le unità presenterebbero la stessa modalità. Viceversa
a valori elevati di R corrisponde una elevata dispersione.
Esempio: intensità dei 15 maggiori terremoti (scala Richter) nel periodo 1983-1991:
5,5
7,7
7,1
7,8
8,1
7,3
6,5
7,3
6,8
6,9
6,3
6,5
7,7
7,7
6,8
Il campo di variazione risulta R=8.1-5.5=2.6. Esso ci dice che il 100% delle scosse di
terremoto è stata di un'intensità compresa fra 5,5 e 8,1.
Se avessimo avuto:
5,5
6,3
6,3
6,3
6,3
6,3
6,3
6,3
6,3
6,3
6,3
6,3
6,3
7,1
8,1
il campo di variazione sarebbe stato lo stesso, anche se la prima distribuzione fosse
molto più variabile della seconda.
Infatti mettiamo a confronto i diagrammi ramo-foglia e vediamo che la seconda
distribuzione è estremamente concentrata intono a 6,3 mentre la prima distribuzione è
molto più dispersa.
Distribuzione A
5
6
7
8
5
3 5 5 8 8 9
1 3 3 7 7 7 8
1
Distribuzione B
5
6
7
8
5
3 3 3 3 3 3 3 3 3 3 3 3
1
1
Osservazioni: L’indice R ha il grande pregio di essere facilissimo da calcolare e di
consentire una immediata interpretazione. D’altro lato ha l’enorme
difetto di essere estremamente sensibile ai valori estremi della
distribuzione (proprio perché è calcolato a partire da essi). Inoltre, come
si è visto dall’esempio sopra, possiamo avere due distribuzioni con
uguale campo di variazione ma variabilità effettiva molto diversa.
1
Corso di Statistica (canale A – D)
Dott.ssa P. Vicard
Un’alternativa al campo di variazione è data dallo scarto interquartile (o differenza
interquartile) che si indica con W. Esso è dato dalla differenza tra il terzo quartile e il
primo quartile. In formule
W = Q3 − Q1
Lo scarto interquartile rappresenta una misura più rappresentativa della variabilità di
un carattere rispetto al campo di variazione. W dà l’intervallo di valori all’interno del
quale cade il 50% delle osservazioni.
W ha il difetto di potere essere nullo anche in presenza di variabilità
Esempio (continuazione dell’es. dei terremoti). Consideriamo la prima distribuzione e
scriviamola in forma di distribuzione di frequenza
xi
5,5
6,3
6,5
6,8
6,9
7,1
7,3
7,7
7,8
8,1
Totale
ni
1
1
2
2
1
1
2
3
1
1
15
fi
0,067
0,067
0,133
0,133
0,067
0,067
0,133
0,199
0,067
0,067
1
Fi
0,067
0,134
0,267
0,400
0,467
0,534
0,667
0,866
0,933
1
Q1 = 6,5
Q3 = 7,7
Allora lo scarto interquartile risulta W=7.7-6.5. Questo vuol dire che il 50% delle
scosse di terremoto hanno avuto un'intensità compresa fra 6,5 e 7,7.
Consideriamo la seconda distribuzione
xi
5,5
6,3
7,1
8,1
Totale
ni
1
12
1
1
15
fi
0,067
0,799
0,067
0,067
1
Fi
0,067
0,866
0,933
1
In questo caso è:
Q1 = 6,3
Q3 = 6,3
Lo scarto interquartile risulta W=6.3-6.3=0. Questo vuol dire che il 50% delle
scosse di terremoto hanno avuto la stessa intensità.
2
Corso di Statistica (canale A – D)
Dott.ssa P. Vicard
Esempio: contenuto effettivo in cc di 100 bottiglie imbottigliate con un procedimento
automatico.
Contenuto in
cc
730 – 740
740 – 748
748 – 752
752 – 760
760 – 770
Totale
ni
fi
Fi
12
20
39
21
8
100
0,12
0,20
0,39
0,21
0,08
1
0,12
0,32
0,71
0,92
1
748 − 740
(0,25 − 0,12) = 745,2
0,20
760 − 752
Q 3 = 752 +
(0,75 − 0,71) = 753,52
0,21
Q1 = 740 +
Lo scarto interquartile risulta:
W = 753,52 − 745,2 = 8,32
evidenziando che il 50% delle bottiglie hanno un contenuto effettivo compreso fra
745,2 cc e 753,52 cc.
IL BOX-PLOT
Una descrizione sintetica e abbastanza completa di una distribuzione di frequenze
secondo un carattere quantitativo è data dal box-plot; questo è un riassunto a cinque
numeri. I numeri sono i seguenti:
- la mediana (che dà informazioni sulla tendenza centrale)
- il primo e terzo quartile (la cui differenza dà informazioni sulla variabilità)
- i due estremi (la modalità più grande e la modalità più piccola)
Questi numeri forniscono una descrizione sintetica di un insieme di dati anche quando
il numero di unità osservate è elevato.
Consideriamo nuovamente l’esempio dei terremoti e in particolare la distribuzione
xi
5,5
6,3
6,5
6,8
6,9
7,1
7,3
7,7
7,8
8,1
Totale
ni
1
1
2
2
1
1
2
3
1
1
15
fi
0,067
0,067
0,133
0,133
0,067
0,067
0,133
0,199
0,067
0,067
1
Fi
0,067
0,134
0,267
0,400
0,467
0,534
0,667
0,866
0,933
1
3
Corso di Statistica (canale A – D)
Dott.ssa P. Vicard
Il box-plot è dato da:
25%
5,5
↑
Min
25%
6,5
↑
Q1
25%
25%
7,1
↑
Me
7,7
↑
Q3
8,1
↑
Max
Il box-plot è utile perché riassume mediante pochi numeri molte informazioni su una
distribuzione di frequenze.
La mediana riassume la tendenza centrale della distribuzione.
I quartili danno un’indicazione sulla variabilità, perché con essi si calcola lo scarto
interquantile (misura più robusta del campo di variazione).
La posizione della mediana rispetto ai quartili fornisce altre utili informazioni (in
particolare sulla asimmetria della distribuzione, che si vedrà nelle prossime lezioni).
Gli estremi forniscono indicazioni non solo sul valore massimo e valore minimo ma
soprattutto sull’eventuale presenza di dati con caratteristiche anomale (al limite
impossibili) dovute ad errori di misura, di trascrizione,…
Descriviamo più in dettaglio il disegno del box-plot.
Esso è la rappresentazione grafica che si associa al riassunto a cinque numeri.
Si costruisce nel modo seguente:
- Si traccia un asse orizzontale (scala del carattere) al di sopra del quale viene
disegnato il diagramma
- Si disegna un rettangolo (la scatola) che ha il primo e il terzo quartile come
estremi della base (cioè la base del rettangolo è uguale allo scarto interquartile).
L’altezza del rettangolo è arbitraria.
- Si traccia, all’interno del rettangolo, una linea verticale in corrispondenza della
mediana.
- si tracciano due linee verticali (di altezza uguale o minore all’altezza del
rettangolo) in corrispondenza del valore massimo e del valore minimo. Questi due
segmentini vengono detto “baffi” del box-plot.
- Infine si tracciano due linee orizzontali che collegano i “baffi” al rettangolo.
Il box-plot è un’ottima sintesi ma comunque non ci dice come si distribuiscono
esattamente le osservazioni tra un quartile e un altro. Il box-plot ci dà un'idea generale
della dispersione e della asimmetria della distribuzione.
D'altro lato, il box-plot è una rappresentazione grafica molto utile quando si vogliono
mettere a confronto due o più distribuzioni.
4
Corso di Statistica (canale A – D)
Dott.ssa P. Vicard
Esempio: riprendiamo l’esempio dei redditi negli USA delle famiglie bianche e delle
famiglie di colore.
Di seguito riportiamo la tabella con i dati
Reddito
(in migliaia di $)
0–5
5 – 10
10 – 15
15 – 25
25 – 35
35 – 50
Totale
Famiglie Bianche
fi
Fi
0.07
0.12
0.13
0.24
0.21
0.23
1
0.07
0.19
0.32
0.56
0.77
1
Famiglie di Colore
fi
Fi
0.16
0.19
0.15
0.23
0.14
0.13
1
0.16
0.35
0.50
0.73
0.87
1
Per effettuare meglio il confronto, si rappresentano i box-plot nello stesso grafico e
generalmente vengono disposti in modo verticale. I cinque numeri sono:
Min
Q1
Me
Q3
Max
Famiglie Bianche
0
12.3
22.5
34.05
50
Famiglie di Colore
0
7.37
15
26.43
50
0
R
E
D
D
I
25
T
O
50
Famiglie
Bianche
Famiglie di
Colore
5
Corso di Statistica (canale A – D)
Dott.ssa P. Vicard
Come individuare valori anomali nella distribuzione.
I valori anomali di una distribuzione si possono individuare in modo semplice come
segue.
Un dato è anomalo se:
- è più alto del valore Q3 + 1.5 W
- è più basso del valore Q1 − 1.5 W
Un dato è estremo (estremamente anomalo) se
- è più alto del valore Q3 + 3 W
- è più basso del valore Q1 − 3 W
Questi valori una volta individuati possono poi essere indicati sul box-plot.
Sono osservazioni che NON vanno cancellate in quanto “molto lontane” e “molto
differenti” dalle altre. Occorre innanzitutto capirne la ragione e quindi studiarle.
Esse, infatti, potrebbero essere dovute
i)
o ad errori nella fase di raccolta dati (trascrizione o interpretazione errata
della domanda)
ii)
o ad errori in fase di registrazione dei dati su computer
iii)
o a segnali importanti che arrivano in merito al fenomeno oggetto di
interesse. Potrebbe essere un segno di cambiamento o di un qualche
distorsione che inizia d agire sul fenomeno. In questo caso le osservazioni
non vanno cancellate.
6
Corso di Statistica (canale A – D)
Dott.ssa P. Vicard
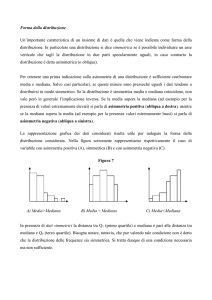
Forma della distribuzione
La terza caratteristica dei dati che prendiamo in considerazione è la forma della loro
distribuzione, ovvero il modo in cui si distribuiscono le nostre osservazioni.
In particolare cercheremo di individuare un criterio per definire cosa si intende per
distribuzione simmetrica e in seguito si proporranno degli indici per misurare gli
scostamenti dalla situazione di simmetria.
Innanzitutto per effettuare lo studio della simmetria è necessario che il carattere
rilevato sia almeno qualitativo ordinato.
Un esempio di distribuzione simmetrica è il seguente
X
ni
1
2
3
4
5
6
7
2
5
8
11
8
5
2
Come si vede K=7 e n1 = n7 = 2, n 2 = n 6 = 5, n3 = n5 = 8, n 4 = 11
Vediamo il grafico
Simmetria
12
10
8
6
4
2
0
1
2
3
4
5
6
7
Consideriamo la generica distribuzione di frequenze dove X è almeno qualitativo
ordinato.
X
ni
x1
n1
x2
n2
...
...
xk
nk
TOTALI
n
Diciamo che la distribuzione è simmetrica se la variabile assume valori equidistanti
dal centro di simmetria con uguale frequenza.
Per es. nel caso in cui il carattere X abbia K modalità equidistanti fra loro, la
distribuzione è simmetrica se n1 = nK, n 2 = nK −1, n 3 = nK − 2, K
7
Corso di Statistica (canale A – D)
Dott.ssa P. Vicard
Si vede che il numero di unità che presentano le unità più basse è lo stesso del numero
di unità che presentano le modalità più alte.
Quando abbiamo una distribuzione in cui: o è maggiore il numero di unità che
presentano le modalità più basse o è maggiore il numero di unità che presentano le
modalità più alte, si parla di distribuzioni asimmetriche.
Vediamo le due seguenti distribuzioni.
Distribuzione 1
Distribuzione 2
X
ni
X
ni
1
2
3
4
5
6
7
7
11
8
5
3
2
0,5
1
2
3
4
5
6
7
0,5
2
3
5
8
11
7
Vediamo che nessuna delle due verifica la definizione di simmetria.
Esse hanno però caratteristiche diverse.
La distribuzione 1 mostra che la maggior parte delle unità presenta valori bassi del
carattere (si parla di asimmetria positiva); la distribuzione 2, invece, mostra che la
maggior parte delle unità presenta valori elevati del carattere (si parla di asimmetria
negativa). Vediamo le rappresentazioni grafiche
Asimmetria positiva
12
10
8
6
4
2
0
1
2
3
4
5
6
7
6
7
Asimmetria Negativa
12
10
8
6
4
2
0
1
8
2
3
4
5
Corso di Statistica (canale A – D)
Dott.ssa P. Vicard
Dai grafici si vede chiaramente che
Ø nel caso di asimmetria positiva le osservazioni sono più addensate in
corrispondenza dei valori più bassi
Ø nel caso di asimmetria negativa le osservazioni sono più addensate in
corrispondenza dei valori più alti.
La mediana gioca un ruolo estremamente importante nell’analisi della simmetria; essa
infatti è la modalità che divide in due parti uguali la distribuzione lasciando alla sua
sinistra e alla sua destra il 50% delle osservazioni.
Nota: è la definizione stessa di simmetria di una distribuzione a essere imperniata
sulla mediana. Infatti una distribuzione si dice simmetrica se le modalità
equidistanti dalla mediana hanno la stessa frequenza.
Indici di asimmetria
Data una distribuzione, abbiamo bisogno di opportuni indici per misurare se e quanto
essa si discosta dalla situazione di simmetria; in sostanza misuriamo la asimmetria di
una distribuzione come deviazione dalla situazione di simmetria.
Innanzitutto gli indici di asimmetria dovrebbero essere pari a zero se e solo se la
distribuzione è simmetrica. Purtroppo però gli indici di asimmetria che vedremo non
godono di questa proprietà; in particolare se la distribuzione è simmetrica essi sono
nulli ma non è vero il viceversa, cioè se l’indice di asimmetria è pari a zero la
distribuzione potrebbe non essere simmetrica.
Dal momento che la mediana ha un ruolo importante, il primo indice di asimmetria
che vediamo si basa proprio sulla mediana.
Questo indice pone a confronto le seguenti quantità:
Me – Q1
Q3 - Me
Infatti se una distribuzione è simmetrica allora il primo e il terzo quartile sono
equidistanti dalla mediana perché per definizione tra Q1 e Me e tra Me e Q3 sappiamo
esserci lo stesso numero di osservazioni.
Allora consideriamo la differenza: (Q 3 - Me ) − (Me - Q 1 )
Sappiamo che tra il primo quartile e la mediana per definizione cade il secondo 25%
delle osservazioni e tra la mediana e il terzo quartile cade il terzo 25% delle
osservazioni. Abbiamo i seguenti casi:
1. Se (Q3 - Me ) > (Me - Q1 ) vuol dire che le unità sono più addensate (fitte e
concentrate) tra il primo quartile e la mediana perché in un intervallo più piccolo
(quello tra primo quartile e mediana) cade la stessa percentuale di osservazioni. In
altre parole in questa situazione sono maggiori le frequenze che competono alle
modalità più piccole della mediana (e maggiori di Q1 ) e quindi siamo nel caso
della asimmetria positiva (quantomeno con riferimento al 50% centrale della
distribuzione).
2. Se (Q3 - Me ) < (Me - Q1 ) vuol dire che le unità sono più addensate (fitte e
concentrate) tra la mediana e il terzo quartile perché in un intervallo più piccolo
cade la stessa percentuale di osservazioni. In altre parole in questa situazione sono
9
Corso di Statistica (canale A – D)
Dott.ssa P. Vicard
maggiori le frequenze che competono alle modalità più grandi della mediana (e
minori di Q3 ) e quindi siamo nel caso della asimmetria negativa (quantomeno con
riferimento al 50% centrale della distribuzione).
3. Se (Q 3 − Me) = (Me - Q1 ) vuol dire che la stessa frazione di unità (il 25%) cade in
due intervalli di uguale ampiezza, cosa che fa pensare ad una situazione di
simmetria (almeno per quanto riguarda le unità comprese tra il primo e il terzo
quartile).
La differenza considerata dipende dall’unità di misura e quindi al suo posto si
preferisce usare l’indice
λ=
(Q3 - Me ) − (Me - Q1 )
Q 3 - Q1
=
Q3 + Q1 − 2Me
Q 3 - Q1
che è un indice relativo cioè non dipende dall’unità di misura e assume valori tra –1 e
+1 (estremi inclusi). In particolare
- valore massimo +1 quando Me = Q1 e quindi Me – Q1 = 0 e Q3 – Me = Q3 – Q1
- valore minimo –1 quando Me = Q3 e quindi Q3 – Me = 0 e Me – Q1 = Q3 – Q1
In sostanza questo indice va a misurare ciò che si osserva mediante il box-plot quando
si pone l’attenzione alla scatola e si vede se la linea che rappresenta la mediana è nel
centro della scatola (e allora si ha simmetria) oppure è più vicina al primo quartile (e
allora si ha asimmetria positiva) oppure è più vicina al terzo quartile (e allora si ha
simmetria negativa).
Esempio: consideriamo di nuovo l’esempio dei redditi delle famiglie statunitensi che
abbiamo visto nella sezione dedicata al box-plot.
Riportiamo di nuovo i quartili relativi ai due gruppi di famiglie
Famiglie Bianche
12.3
22.5
34.05
Q1
Me
Q3
Famiglie di Colore
7.37
15
26.43
Dai due box-plot vediamo che c’è una situazione di asimmetria positiva in entrambe
le distribuzioni visto che la linea che rappresenta la mediana non si trova nel centro
della scatola ma è un po’ spostata verso il primo quartile. Inoltre si osserva,
comparando i due box-plot, che l’asimmetria positiva è più accentuata nella seconda
distribuzione dove nella scatola la linea che rappresenta la mediana è più spostata
verso il primo quartile di quanto non lo sia nella prima distribuzione.
Verifichiamo queste affermazioni con il calcolo degli indici di asimmetria
λ1 =
λ2 =
10
(Q 3 - Me ) − (Me - Q1 )
Q 3 - Q1
(Q3 - Me ) − (Me - Q1 )
Q3 - Q1
=
Q 3 + Q1 − 2Me 34.05 + 12.3 − 2 ⋅ 22.5
=
= 0.062
Q 3 - Q1
34.05 − 12.3
=
Q3 + Q1 − 2Me 26.43 + 7.37 − 2 ⋅ 15
=
= 0.112
Q3 - Q1
26.43 − 7.37
Corso di Statistica (canale A – D)
Dott.ssa P. Vicard
Anche il calcolo dell’indice di asimmetria mostra che la seconda distribuzione è più
asimmetrica della prima.
Osservazione : λ=0 anche quando la distribuzione è asimmetrica.
Ad esempio si prenda la distribuzione
X
fi
Fi
3
0.1
0.1
5
0.17
0.27
7
0.26
0.53
9
0.33
0.86
10
0.14
1
Si vede che Q1 = 5, Me = 7 e Q3 = 9 quindi
(9 − 7 ) − (7 − 5 ) = 0
λ=
9−5
Osservando le frequenze vediamo che la distribuzione è tutt’altro che simmetrica ma
mostra una maggiore concentrazione delle unità intorno a valori grandi del carattere
X.
Osservazione : un altro problema di questo indice è che è poco sensibile perché è
basato sui tre quartili e non tiene conto di tutti i valori assunti dal carattere nelle unità
del collettivo.
Supponiamo di avere una distribuzione unimodale di un carattere quantitativo.
Abbiamo che se la distribuzione è simmetrica allora la media, la moda e la mediana
coincidono.
C’è da notare che non è detto che sia vero il viceversa cioè si possono avere
distribuzioni per le quali media = moda = mediana ma la distribuzione non è
simmetrica.
Si consideri ad esempio la distribuzione seguente
X
2
8
10
15
Totale
ni
1
1
3
2
7
Fi
0.14
0.29
0.71
1
Essa è palesemente negativamente asimmetrica ma ha
Mo = 10
µ = (2+8+10⋅3+15⋅2)/7 = 10
Me = 10
Cioè i suoi tre valori medi coincidono.
Da questo esempio già si può capire che l’indice che andiamo a proporre, un indice
che mette a confronto la media e la moda, potrà essere nullo anche quando la
distribuzione non è simmetrica. In altre parole anche questo indice avrà lo stesso
difetto dell’indice λ visto sopra.
Pertanto quando abbiamo una distribuzione unimodale si ha che
- se è simmetrica allora µ = Me = Mo
11
Corso di Statistica (canale A – D)
-
-
Dott.ssa P. Vicard
se è positivamente asimmetrica allora µ > Me > Mo. In altre parole l’asimmetria
positiva si presenta quando la media è più elevata della mediana e della moda per
la presenza di valori particolarmente alti
se è negativamente asimmetrica allora µ < Me < Mo. In altre parole l’asimmetria
negativa si presenta invece quando la media è inferiore alla mediana e alla moda
per la presenza di valori particolarmente piccoli.
Possiamo prendere come misura di asimmetria un indice che si basa sulla differenza
tra media aritmetica e moda µ - Mo. Questa differenza dipende dall’unità di misura
con cui è misurato il carattere pertanto, per ottenere un numero “puro”, la si divide per
lo scarto quadratico medio. In questo modo si ottiene l’indice di asimmetria (proposto
da K. Pearson)
µ − Mo
sk =
σ
detto skewness di Pearson.
Se l’asimmetria è spiccatamente positiva allora sk > 0.
Se l’asimmetria è spiccatamente negativa allora sk < 0.
Sia λ che sk possono essere nulli anche quando la distribuzione non è simmetrica.
Inoltre essi generalmente sono in grado di segnalare solamente situazioni di evidente
asimmetria, cioè non sono molto sensibili alle deviazioni della distribuzione dalla
simmetria perché dipendono solo da valori di sintesi della distribuzione.
Pearson ha proposto anche un altro indice per lo studio della asimmetria. Questo si
basa sul fatto che in una distribuzione simmetrica tutti i momenti di ordine dispari
dalla media aritmetica sono nulli.
I momenti dalla media aritmetica sono definiti così:
1n
µ r = ∑ (ai − µ )r quando si ha una distribuzione per unità
n i =1
1K
µ r = ∑ (x i − µ )r ni quando si ha una distribuzione di frequenze
n i =1
Notare che per r = 2, µ 2 = σ2 .
1K
Indichiamo con µ 3 = ∑ (x i − µ )3 ni il momento di ordine 3 dalla media aritmetica.
n i =1
Questo, se la distribuzione è simmetrica, è nullo.
Se l’asimmetria è sensibilmente positiva allora µ 3 > 0 perché prevalgono gli
scostamenti positivi dalla media dovuti anche alla presenza di valori eccezionalmente
alti.
Se l’asimmetria è sensibilmente negativa allora µ 3 < 0 perché prevalgono gli
scostamenti negativi dalla media dovuti anche alla presenza di valori eccezionalmente
bassi.
Per rendere l’indice indipendente dall’unità di misura (il momento terzo dalla media
aritmetica è espresso nell’unità di misura alla terza) basta dividerlo per lo scarto
quadratico medio elevato alla terza. In questo modo si ottiene l’indice seguente:
µ
β = 33
σ
Anche β può essere nullo anche se la distribuzione non è simmetrica.
12
Corso di Statistica (canale A – D)
Dott.ssa P. Vicard
Esempio: Consideriamo dati relativi al rendimento percentuale a un anno di 17 fondi
di investimento. Abbiamo questi dati in forma di distribuzione unitaria;
32.2 29.5 29.9 32.4 30.6 30.1 32.1 35.2 10.0 20.6 28.6 30.5 38.0 33.0
29.4 37.1 28.6
Ordiniamo le osservazioni
10.0 20.6 28.6 28.6 29.4 29.5 29.9 30.1 30.5 30.6 32.1 32.2 32.4 33.0
35.2 37.1 38.0
Abbiamo:
Mo = 28.6
µ = 507.8/17 = 29.87
σ2 = 15826.98/17 – 29.872 = 38.78
σ = 6.23
Quindi sk = (29.87-28.6)/6.23 = 0.204
Per esercizio si calcoli l’indice β.
13