Sintesi dei dati
La sintesi dei dati comporta una perdita di
informazioni, deve quindi essere privilegiato
l’indice di sintesi che minimizza la perdita e
rappresenta nel modo più corretto l’insieme
dei dati osservati
1
Indice di sintesi
deve essere compresa tra il dato più piccolo ed il dato più
elevato della distribuzione
x1 ≤ sintesi ≤ xn
deve identificarsi con i valori più frequenti
sono localizzati al centro della distribuzione
indici di “tendenza centrale”
2
Indici di sintesi:
medie analitiche: il calcolo richiede operazioni algebriche
su tutti i valori del carattere
dati quantitativi
indici di posizione: il calcolo non considera tutti i valori
ma solo la loro posizione
tutti i tipi di dati
3
MEDIA ARITMETICA
N
X
i 1
i
N
Calcolabile per dati quantitativi continui
4
Esempio sulla media aritmentica
Peso di un campione di n=60 casse di legno
presenti in porto da caricare su nave merci
19,
25,
24,
19,
20,
29,
26,
19,
20,
24,
15,
17,
20,
20,
24,
20,
19,
24,
25,
26,
20, 17, 25, 15,
21, 22, 24, 23,
24, 25, 26, 25,
26, 24, 24, 20,
24, 24, 26, 24
26,
19,
19,
20,
25,
20,
19,
26,
17,
21,
25,
26,
21,
26,
19,
20,
22,
26,
26,
24,
N
X
i 1
N
i
Somma delle x = 1341
Media = 1341/60 = 22.35 Kg
5
INDICI DI POSIZIONE
forniscono indicazioni sulla tendenza centrale di una
distribuzione, senza ricorrere all’elaborazione di tutti i
dati
sono utilizzabili:
per i dati qualitativi ordinali
per i dati quantitativi
6
MODA
è quel valore che corrisponde alla massima frequenza del
fenomeno
può essere utilizzata:
per dati qualitativi
per dati quantitativi discreti
per dati quantitativi continui ma divisi in classi
non prende in considerazione i dati relativi ad un
carattere, ma le frequenze con cui i dati del carattere
osservato si presentano (nessuna operazione algebrica)
7
Esempio:
Numero di
viaggi negli
ultimi 5 anni
F
0
1
1
2
2
3
4
5
3
1
5
Totale
1
13
8
MEDIANA
utilizzata quando:
dati qualitativi, oppure quantitativi ordinati in senso
crescente o decrescente
Valori anomali
valore che occupa la posizione centrale
divide in due parti uguali la distribuzione
il 50% dei dati sono di valore superiore a quello della
mediana ed il 50% di valore inferiore
9
Mediana
Calcolo:
Se N è dispari
Mediana = dato che occupa la posizione (N+1)/2
tale che la metà dei valori è rispettivamente maggiore e minore
rispetto al valore della mediana
Se N è pari
Mediana = dati nella posizione N/2 ed ( N /2 ) + 1*
* nel caso in cui i dati siano quantitativi, la mediana è data dalla
media dei due valori centrali della distribuzione
10
Esempio:
Autotrasportatori che alloggiano in albergo
Categoria n°autisti
1 Stella
391
2 Stelle
1875
3 Stelle
8922
4 Stelle
2443
5 Stelle
218
Tot
13849
Moda=
3 stelle
Posto mediano=(13849+1)/2=
Mediana=3 stelle
6925
10000
9000
8000
7000
6000
5000
4000
3000
2000
1000
0
8922
2443
1875
391
1 Stella
218
2 Stelle
3 Stelle
4 Stelle
5 Stelle
11
Quantili
QUANTILI: valori che dividono la distribuzione in parti uguali
Assumono denominazioni diverse a seconda del numero di parti in cui suddividono
l’insieme delle unità ordinate per grandezza
QUARTILI: valori per cui una distribuzione, ordinata in senso crescente, risulta
suddivisa in 4 parti uguali
Il primo quartile (Q1) è quel valore che lascia a sinistra il 25% della distribuzione ed
il 75% a destra
Il secondo quartile (Q2) corrisponde con la mediana e lascia destra ed a sinistra il
50% dei dati;
Il terzo quartile (Q3), è quel valore che lascia a destra il 25% della distribuzione ed il
75% a sinistra
CENTILI: In una distribuzione si calcola la distribuzione cumulativa della
frequenza relativa per una certa variabile X.
Il valore xi che separa l’1% delle osservazioni è chiamato primo centile, il valore xi
che separa il 2% delle osservazioni è il secondo centile e così via.
Il 500 centile corrisponde alla mediana della distribuzione
12
Box-Whisker plot
mediana (50° percentile)
75° percentile
25° percentile
massimo
minimo
25
50
75
100
mesi
13
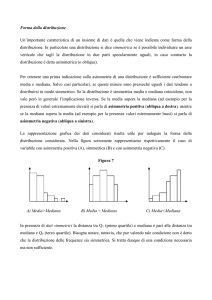
Distribuzione Simmetrica
μ = Me = Mo
14
Distribuzione con asimmetria positiva
Mo < Me < μ
15
Distribuzione con asimmetria negativa
μ < Me < Mo
16
Simmetria e Asimmetria
Se la distribuzione è simmetrica
μ = Me = Mo
Se μ = Me = Mo
la distribuzione è simmetrica
La condizione dell’uguaglianza delle tre misure è necessaria, ma
non sufficiente, a garantire la simmetria di una distribuzione
infatti, data la seguente distribuzione:
4, 16, 20, 20, 20, 30, 30
30
media = 20
25
mediana = 20
20
moda =20
15
10
5
la distribuzione è asimmetrica!!!
0
17