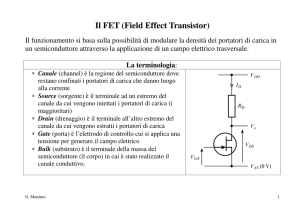
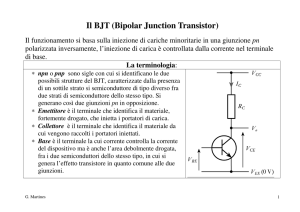
La struttura metallo-ossido-semiconduttore
➢
➢
➢
➢
➢
TOX è lo spessore dell'ossido (il dielettrico)
vG è la tensione del gate rispetto a massa
a regime, la carica accumulata nel gate
deve essere bilanciata dalla carica presente
alla interfaccia fra ossido e semiconduttore
(la seconda armatura del condensatore)
il valore VTH di vG, è la tensione di soglia
(threshold voltage) in corrispondenza a cui
la concentrazione dei portatori minoritari alla interfaccia ossido-silicio supera quella dei portatori
maggioritari nel substrato
superata la tensione di soglia esiste lo strato di inversione
In questa figura e nelle successive:
✗ il substrato è di tipo p (portatori maggioritari le lacune),
✗ lo strato di inversione è quindi equivalente ad un materiale di tipo n
✗ viene descritto il meccanismo di funzionamento di un MOS a canale n ad arricchimento
✗ la tensione di soglia è VTN perchè si crea uno strato di inversione di tipo n
G. Martines
1
Regione di accumulazione, svuotamento, inversione
Regione di accumulazione: VG << VTN
Regione di svuotamento: VG < VTN
Regione di inversione: VG > VTN
NOTA: in regione di inversione l'eccesso di
portatori minoritari nasce dalla generazione
di coppie elettrone-lacuna nella regione di
svuotamento.
G. Martines
2
MOSFET a canale n ad arricchimento
L = Lunghezza e W = Larghezza di canale
terminali: S = Source , D = Drain , G = gate , B = body
S
D
n
p
n
G. Martines
3
MOSFET a canale n ad arricchimento
Analisi qualitativa (VDS = 0 V)
G. Martines
4
MOSFET a canale n ad arricchimento
Analisi qualitativa in regione lineare (VDS ∼ 0 V)
i S =i D perché iG è quella di una capacità a regime ed
iB quella di una giunzione pn polarizzata inversamente
➔ per x che tende a 0 anche v(x) tende a 0
➔ per x che tende a L invece v(x) tende a vDS
➔ v OX =v GS v( x) ma per avere inversione v OX ≥V TN
allora si definisce tensione di overdrive la quantità
v OV =v GS V TN
Per v DS ≪v GS V TN si può dire che vOX è costante e quindi
l'andamento del canale è quello indicativamente mostrato in
figura.
Si può dimostrare che in queste condizioni il comportamento è ohmico.
➔
G. Martines
5
MOSFET a canale n ad arricchimento
Analisi qualitativa in regione di triodo (VDS ≠ 0 V)
Per v DS ≤v GS V TN l'andamento del canale è quello di
figura poiché vOX varia con x in questo caso.
si può dimostrare che
1
i D =K n [(v GS V TN ) v DS v 2DS ] con K n =µ n C OX W
2
L
dove C OX =OX /T OX è la capacità dell'ossido per unità di
area ed εOX la costante dielettrica dell'ossido.
G. Martines
6
MOSFET a canale n ad arricchimento
Analisi in regione di saturazione (v DS ≥v GS V TN )
per v DS =v GS V TN il pinch-off si ha per x=L e la
K
corrente è espressa da i D = n (v GS V TN )2
2
per v DS >v GS V TN il pinch-off si ha per x<L ma la
corrente non può aumentare perché il flusso di carica è
limitato dalla velocità di deriva degli elettroni.
G. Martines
7
MOSFET a canale n ad arricchimento
Le caratteristiche iD-vDS
un esempio in
regione lineare
Andamento di una singola caratteristica con le equazioni
finora presentate.
G. Martines
8
MOSFET a canale n ad arricchimento
Le caratteristiche iD-vDS
La trans-caratteristica
del transistore in
regione di saturazione
G. Martines
9
MOSFET a canale n ad arricchimento
Il circuito equivalente a largo segnale in saturazione
dove k ' n =µn C OX ed r o=
1
λID
I simboli circuitali più comuni
G. Martines
10
MOSFET a canale n ad arricchimento
Effetto di modulazione della lunghezza del canale
la variazione è proporzionale: ∆ L=λ ' v DS e λ=λ ' / L
l'espressione della corrente di drain in saturazione:
1
W
i D = µ n C OX (v GS V TN )2 (1+λ V DS )
2
L
G. Martines
11
MOSFET a canale n a svuotamento
(NMOS DE)
G. Martines
12
MOSFET a canale p ad arricchimento
G. Martines
13
MOSFET a canale p ad arricchimento
I simboli circuitali più comuni
Altri simboli comunemente usati per i vari tipi di MOSFET:
G. Martines
14
Esempio di tecnologia CMOS
Transistori MOS a canale n ed a canale p realizzati sullo stesso substrato di tipo p.
G. Martines
15
Amplificatore di tensione con MOSFET
Andamento di vO per vGS che varia fra 0 e VDD per il circuito mostrato:
1
v DS =V DD i D R D e v DS =V DD K n (v GS V t )2 R D
2
Nota: ∣V GS∣B=V t +
G. Martines
√ 2K n R D V DD+11
K n RD
16
Amplificatore di tensione con MOSFET
È la trans-caratteristica di un amplificatore di tensione con v I =v GS e v O =v DS
Per utilizzare il circuito come amplificatore bisogna polarizzare il transistore per tenerlo in
un punto di riposo come Q.
G. Martines
17
Guadagno di tensione per
piccoli segnali
Pendenza della tangente alla curva nel
punto Q:
∣ ∣
Av ≡
G. Martines
dv DS
dv GS
=K n (V GS V t ) R D
V GS
18
Amplificatore di tensione con MOSFET
Rappresentazione nel piano delle caratteristiche di uscita
con il metodo della curva di carico
Scelta del punto di riposo Q con riferimento al guadagno:
Av =K n (V GS V t ) R D=K n V OV R D
2I R
ricordando che I D = 1 K n V 2OV si ottiene Av = D D
V OV
2
(ma ID e VOV non sono indipendenti!) e si può definire
l'espressione del massimo:
∣Avmax∣=
G. Martines
V DD
V OV /2
19
Amplificatore di tensione con MOSFET
Forme d'onda sul gate e sul drain del dispositivo
Scelta del punto di riposo Q in funzione dell'escursione del
segnale di uscita e dell'ampiezza del segnale di ingresso
G. Martines
20
Amplificatore di tensione con MOSFET
Criterio di progetto: se si fissa il guadagno di tensione Av e
la ampiezza in uscita V O = I D R D allora
2
2V O
2VO
Av
V OV =
=
ed R D=
2
Av
K n V OV 2K n V O
Ma deve essere contemporaneamente
V DSQ =V DD V O ≥V O+V OV
per avere un segnale di uscita di ampiezza VO.
G. Martines
21
Modello equivalente a piccolo segnale
del FET
Si basa sulla assunzione: v GS =V GS +v gs
1
da cui discende i D= K n (V GS +v gs V t )2
2
1
i D = K n [(V GS V t )2+2(V GS V t )v gs +v 2gs ]
2
che diviene
1
i D≈ K n (V GS V t )2 + K n (V GS V t )v gs = I D +i d
2
per
v gs ≪2(V GS V t )
Allora
g m≡
id
= K n (V GS V t )=K n V OV
v gs
∣ ∣
∂id
che equivale a g m≡
∂ v gs
G. Martines
v GS =V GS
22
Modello equivalente a piccolo segnale del FET
Per tenere in conto la dipendenza di iD da vDS si
introduce la resistenza incrementale
1
r O=
λ ID
Altre espressioni per la transconduttanza:
2I D
g m= K n V OV =√ 2K n I D =
V OV
Il Fattore di Amplificazione µf o guadagno di tensione intrinseco è una figura di merito
che esprime il valore massimo del guadagno di tensione ottenibile, in base al circuito
equivalente a piccolo segnale del transistore:
2
1 2K n
µ f = g m r o=
=λ
λ(V GS V t )
ID
√
Per i MOSFET è inversamente proporzionale alla radice quadrata della corrente di drain
nel punto di lavoro.
G. Martines
23
Modello equivalente a piccolo segnale
dell'amplificatore
Nell'analisi a piccolo segnale si considerano solo le componenti
variabili dei segnali. Allora tutti i nodi a tensione costante sono
equivalenti al nodo
di massa perché la
componente
variabile della
tensione è nulla.
Se sostituiamo il
simbolo del transistore
con il suo modello
equivalente a piccolo
segnale.
Avs=g m (r o / / R D )
G. Martines
24
Il problema della stabilità del punto di riposo
Polarizzazione a VGS fissa
1
W
i D = µ n C OX (v GS V TN )2 (1+λ V DS )
2
L
L'effetto di una variazione in uno o più parametri del
transistor (possibili anche in dispositivi dello stesso chip)
provoca una variazione della corrente iD elevata.
La resa produttiva con questa tecnica di polarizzazione non
può essere elevata
G. Martines
25
Il problema della stabilità del punto di riposo
Polarizzazione con VG fissa e resistore sul source
La resistenza RS introduce una reazione negativa che desensibilizza la ID rispetto alle
variazioni parametriche essendo V GS =V G I D RS . Se la ID tende ad aumentare per un
qualsiasi motivo, la VGS diminuisce (e viceversa). L'effetto è tanto maggiore quanto
maggiore è RS.
G. Martines
26
Amplificatore invertente elementare con MOSFET
Polarizzazione a quattro resistenze per un NMOS E a CS
L'alimentazione VDD è
unipolare. Le equazioni di
progetto sono:
RG2
V G=
V
(RG1+R G2) DD
V V GS
RS = G
ID
V DS =V DD I D (R D +R S )
Condizioni per la regione di
saturazione con segnale di
uscita di ampiezza VO:
I D R D ≥V O ; V DS V GS +V TN ≥V O ; I D RS =V DD I D R D V DS ; V G =V GS + I D RS
Criterio del 1/3: se le specifiche di ampiezza lo consentono, si assume V O =V DD /3 come
buon compromesso fra escursione del segnale di uscita e stabilità del punto di riposo.
G. Martines
27
Amplificatore invertente con NMOS E
Un esempio di schema circuitale completo di generatore di
segnale equivalente (vI ed RI), di carico (R3) e di capacità di
blocco (C1 e C2) e di bypass (C3)
Polarizzazione a quattro resistenze (R1, R2, RD e RS, R4) ed
alimentazione unipolare (VDD) di un MOSFET in
configurazione common source (CS) con rete di reazione
negativa (RS).
G. Martines
28
Amplificatore invertente con NMOS E
Schema equivalente per l'analisi a piccolo segnale:
circuito equivalente semplificato dell'amplificatore:
G. Martines
29
Amplificatore invertente con FET in CS
La semplificazione è giustificata se la corrente in ro è
trascurabile rispetto a quella del generatore di corrente.
Il guadagno di tensione dell'amplificatore:
v
v v
g m R L
Av = o = o gs =
v g v gs v g 1+ g m R S
Essendo v g =v gs + g m v gs R S
Ovviamente se
mentre se
g m R S ≫1 allora
RS =0 allora
Av =
R L
RS
A v =g m R L
g m R D
Analogamente a vuoto ( R3=∞ ) Avo =
1+ g m R S
Il guadagno di tensione complessivo invece è dato da:
Avs=
G. Martines
(
v o v o v g g m R L
RG
=
=
v i v g v i 1+ g m RS R I + RG
)
30
Amplificatore invertente con FET in CS
Per la determinazione della resistenza di ingresso (Rin):
Si usa il circuito equivalente per l'analisi a piccolo segnale:
il simbolo del transistor viene sostituito con il modello
equivalente per l'analisi a piccolo segnale e si sollecita con
un generatore di tensione per calcolare la corrente in
ingresso
G. Martines
31
Amplificatore invertente con FET in CS
Ovviamente
G. Martines
Ri n= RG =R 1 / / R 2
32
Amplificatore invertente con FET in CS
Per la determinazione della resistenza di uscita (Rout):
si usa il circuito equivalente per l'analisi a piccolo segnale,
con i generatori indipendenti di segnale annullati:
si sostituisce il simbolo del transistor con il modello
equivalente per l'analisi a piccolo segnale, si sollecita con
un generatore di tensione e si calcola la corrente
G. Martines
33
Amplificatore invertente con FET in CS
ix
v gs =v s =i d R S ma i d =g m RS i d +
(v x i d R S )
da cui
ro
vx
RS
=r o (1+ g m R S + ) ed infine
id
ro
RS
)/ / R D
ro
Normalmente è verificata la relazione R S ≪r o e quindi
Rout =r o (1+ g m R S +
Rout ≈r o (1+ g m R S )/ / R D
Ovviamente se manca la controreazione per il segnale, cioè
se R S =0 allora
R out =r o / / R D
Normalmente è verificata la condizione r o ≫ R D ; infatti
I D r o =1/ λ per definizione mentre I D R D <V DD .
G. Martines
34
Amplificatore invertente elementare con MOSFET
Alimentazione bipolare
G. Martines
A due resistenze
Con generatore di corrente
35
Inseguitore di tensione con N MOS E
Si utilizza lo stesso esempio di circuito amplificatore già
Il segnale di uscita viene prelevato dal terminale di Source
anziché da quello di drain.
NOTA: la R3
non ha alcuna
funzione in
questo caso e
quindi il drain
va connesso direttamente alla
alimentazione
nelle applicazioni pratiche.
G. Martines
36
Inseguitore di tensione con N MOS E
Il circuito equivalente a piccolo segnale dello stadio
amplificatore inseguitore di tensione.
dove RG = R 1 / / R 2 mentre R s =R 4 / / R7 .
Con il modello equivalente a piccolo segnale del
transistore, si ottiene un circuito equivalente che è uguale
RI
RG
vg
vgs
gmvgs
vi
RS
G. Martines
ro
vo
37
Inseguitore di tensione con FET in CD
Guadagno di tensione per configurazione common drain
RI
vg
vgs
RG
ro
gmvgs
vi
vo
RS
v o =g m v gs (r o / / R s) e v gs =v g v o
se r o ≫ RS allora v o = g m Rs (v g v o ) cioè
v o (1+g m RS )=g m Rs v g da cui
vo
g R
= m S
v g 1+ g m RS
Ovviamente se g m R S ≫1 allora Av ≈1 .
Av =
g m R4
Avo =
1+ g m R 4
L'espressione completa è invece:
mentre a vuoto ( R7=∞ )
(
vo
g m (r o / / RS )
RG
Avs= =
v i 1+ g m (r o / / RS ) RG + Ri
G. Martines
)
38
Inseguitore di tensione con FET in CD
Calcolo delle resistenze di ingresso Rin e di uscita Rout
Ancora una volta Ri n= R G mentre Rout =R6 / / RiS .
Per valutare RiS il ciurcuito è:
v gs =v x
RI
vg
RG
vgs
ro
gmvgs
ix
vx
vx
i x =g m v gs +
ro
g m r o +1
i x =v x
ro
e quindi
ro
RiS =
1+ g m r o
(
(
)
)
1
Per g m r o ≫1 si riduce a RiS ≈
gm
G. Martines
39
Amplificatore non-invertente con NMOS E
Un esempio di schema circuitale completo di generatore di
segnale equivalente (vI ed RI), di carico (R7) e di capacità di
blocco (C1 e C3) e di bypass (C2)
Polarizzazione a quattro resistenze (R1, R2, R3 e R4) ed
alimentazione
unipolare (VDD) di
un MOSFET in
configurazione
common gate
(CG).
G. Martines
40
Amplificatore non-invertente con NMOS E
circuito equivalente a piccolo segnale dell'amplificatore
CG, semplificato con R L= R 3 / / R7 :
Sostituendo infine il simbolo del transistore con il modello
equivalente a piccolo segnale:
ro
RI
R4
vi
vs
vgs
gmvgs
RL
vo
Circuito equivalente a piccolo segnale a frequenze
intermedie di un amplificatore non-invertente basato su un
singolo FET in configurazione common gate (CG)
G. Martines
41
Amplificatore non-invertente con FET in CG
ro
RI
R4
vs
gmvgs
vgs
RL
vi
vo
Poiché la corrente in ro è normalmente trascurabile rispetto
a quella del generatore di corrente, possiamo trascurarla e
allora per il guadagno di tensione si può scrivere:
v
Av = o =g m R L
vs
Mentre a vuoto ( R 7=∞ )
Avo = g m R3
1
R
=
Analogamente per la resistenza di ingresso i n g
m
Il guadagno di tensione complessivo lo si può scrivere
esprimendo vs con Thevenin:
vo v s
gm RL
R4
Avs=
=
v s v i 1+ g m ( R I / / R4 ) R 4+ R I
(
G. Martines
)
42
Amplificatore non-invertente con FET in CG
Per la resistenza di uscita il circuito equivalente è:
ro
RI
R4
vs
ix
gmvgs
vgs
vx
Non si può trascurare ro altrimenti R out =∞ . Per il calcolo
v x v s
v s=i x ( R I / / R4 ) e i x =
g m v s da cui
ro
vx
1+ g m r o
= 1+
( R I / / R 4) i x e quindi
ro
ro
Rout =r o +(1+ g m r o )( R I / / R4 ) .
Ovviamente g m r o ≫1 e quindi
Rout ≈r o [1+g m ( R I / / R4 )] .
[
G. Martines
]
43
Stadi amplificatori a singolo FET
Riepilogo delle equazioni di progetto
G. Martines
44
Stadi amplificatori a singolo FET
Riepilogo delle prestazioni ottenibili
G. Martines
45
Risposta in frequenza di uno stadio
amplificatore a singolo transistore
Per valutare la risposta in frequenza degli amplificatori si
dovrebbero determinare i poli e gli zeri della funzione di
trasferimento ma risulta complicato sia determinare la
funzione di trasferimento completa che porla in forma
fattorizzata.
Per gli amplificatori a larga banda:
è possibile porre la funzione di trasferimento nella
forma:
T (s ) = AM FL (s )FH (s )
determinare ciascun fattore con il circuito equivalente
appropriato
nell’ipotesi di polo dominante, è possibile determinare
le frequenze di taglio senza conoscere i poli e gli zeri
della funzione di trasferimento.
Il metodo delle costanti di tempo a circuito aperto
(OCTC) permette di determinare la frequenza di taglio fH di
un passa basso nell’ipotesi di polo dominante.
Il metodo delle costanti di tempo in cortocircuito (SCTC)
permette di determinare la frequenza di taglio fL di un passa
alto nell’ipotesi di polo dominante.
Entrambi i metodi forniscono una buona stima delle
frequenze di taglio anche nel caso l’ipotesi non sia
rigorosamente soddisfatta.
G. Martines
46
Metodo delle Costanti di Tempo in
Cortocircuito
fornisce la stima della fL per un circuito passa alto con nL
capacità, nell’ipotesi che sia valida la approssimazione del
polo dominante.
si può dimostrare (Gray e Searle, 1969) che:
dove Ris è la resistenza equivalente vista dai terminali di Ci
quando tutte le altre C → ∞ (cortocircuito).
Nell’ipotesi di polo dominante
e1 = ωL
e quindi:
NOTA: da questa espressione il progettista può rendersi
conto anche di quale sia la capacità che limita la risposta a
bassa frequenza.
G. Martines
47
Risposta a Bassa Frequenza Stadio CS
Il circuito equivalente a piccolo segnale a bassa frequenza è
G. Martines
48
Risposta a Bassa Frequenza Stadio CS
Dalla analisi diretta, si trova che la funzione di
trasferimento del circuito equivalente a bassa frequenza
presenta:
due zeri nell’origine per effetto delle capacità di blocco
uno zero alla risonanza di C3//RE ( ω Z = 1 RE C3 )
tre poli dovuti alle capacità di blocco e di bypass.
Applicando il metodo delle costanti di tempo
in cortocircuito si ottiene:
1
R1S = RS + R1 / / R 2 ; R 2S=R S / /
R = R D / /r o+ R3
g ; 3S
m
e quindi:
1
1
1
ω L≈
+
+
( RS + R1 / / R2 )C 1
1
(R D / /r o+ R3)C 3
(R S / / )C 2
gm
G. Martines
49
Risposta a Bassa Frequenza Stadio CS
In prima approssimazione si può assumere che:
R1S ≈ R1 / / R2 ; R2S≈ R D+ R 3≈ R3 ; R3S≈1 / g m
poiché la resistenza vista dallo emettitore o dal source di un
transistore è più bassa di quelle viste dagli altri terminali,
spesso nel progetto si preferisce rendere dominante il polo
associato a questo terminale (C3 in questo caso) perché le
altre due possono ottenersi facilmente molto maggiori con
valori di capacità dello stesso ordine di grandezza. Quindi
in prima approssimazione si ha
g
f L≈ m .
2 π C2
Nota: il metodo SCTC vale nella ipotesi di polo dominante.
G. Martines
50
Modello ad Alta Frequenza del FET
La capacità di gate è costituita dalla
capacità associata alla Cox e da
quella associata alla regione di
svuotamento della giunzione pn
polarizzata inversamente e può
essere rappresentata da tre capacità
Cgs, Cgd e Cgb.
Indicativamente:
1
C gs =C gd = WLC ox
2
2
C gs = WLC ox
3
in regione di triodo;
in regione di saturazione.
C gd =WL ov C ox≈0
La Cdb viene di solito trascurata mentre
la Cgd , seppure molto piccola (capacità
di sovrapposizione), non può essere
trascurata perché responsabile della
risposta in alta frequenza (effetto
Miller)
G. Martines
51
Modello ad Alta Frequenza del FET
La frequenza di transizione si ottiene come la
frequenza a cui il guadagno di corrente in
cortocircuito del transistore si riduce all'unità. Il
circuito equivalente per il calcolo:
( g msC GD )
I d (s)=( g msC GD )V gs ( s)=I g (s)
da cui
s(C GS +C GD )
sC
g m 1 GD
gm
ωT
s
dove
=
1
β( s)=
s(C GS +C GD )
s
C GS
ω 1+
C GD
(
)
(
(
))
NOTA: il modello è valido fino a frequenze dell’ordine di f T /3 .
G. Martines
52
Metodo delle Costanti di Tempo a
Circuito Aperto
fornisce la stima della fH per un circuito passa basso con nH
capacità, nell’ipotesi che sia valida la approssimazione del
polo dominante.
si può dimostrare (Gray e Searle, 1969) che:
dove Rio è la resistenza equivalente vista dai terminali di Ci
quando tutte le altre C → 0 (circuito aperto).
Nell’ipotesi di polo dominante
b1 = 1/ωH e quindi:
NOTA: da questa espressione il progettista può rendersi
conto anche di quale sia la capacità che limita la risposta ad
alta frequenza.
G. Martines
53
Risposta ad Alta Frequenza Stadio CS
Risposta ad Alta Frequenza Stadio CG
G. Martines
54
Risposta ad Alta Frequenza Stadio CD
Nota: per stadi invertenti e non-invertenti vale comunque
ωH <
G. Martines
1
R L C GD
55