Nome…………………………….Cognome…………………… classe 5C
21 Marzo 2012
Verifica di matematica
1) Considera le curve di equazione f ( x) =
kx 2 − k + 1
x2 +1
con k ∈ R
a) determina i punti comuni a tutte le curve
b) determina k in modo che il grafico sia tangente alla curva di equazione y = 1 − 1 − x 2 nel
suo punto di minimo relativo; studio e rappresenta la funzione così ottenuta.
c) Considera un punto P di ascissa positiva appartenente al grafico di f(x), calcola, in funzione
dell’ascissa del punto l’area del triangolo PHA, dove H indica la proiezione di P sull’asintoto
e A è il punto di coordinate (0;1). Determina quindi il punto P per cui risulta massima l’area
del triangolo.
2) Un settore circolare di raggio 2 è lo sviluppo della superficie laterale di un cono. Determina
l’ampiezza dell’angolo al centro del settore in modo che il cono abbia volume massimo.
3) Su un cartoncino rettangolare si deve applicare una fotografia di 300 cm2 con il margine
superiore e inferiore di 3 cm e con i margini laterali di 4 cm. Che dimensione deve avere il
cartone di area minima che serve allo scopo?
4) Dopo aver enunciato il teorema delle tre perpendicolari, si calcoli la superficie laterale della
piramide ABCV così caratterizzata: la base è il triangolo rettangolo ABC retto in C avente
)
π
AC = 3a e CAB = , altezza VH = a che incontra il lato AC in H con HC = a
3
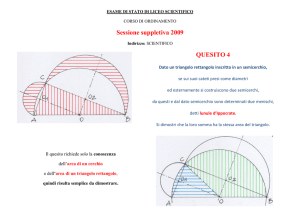
5) Dato un triangolo rettangolo inscritto in un semicerchio, se sui suoi cateti presi come diametri
ed esternamente si costruiscono due semicerchi, da questi e dal dato semicerchio sono
determinati due menischi, dette lunule di Ippocrate. Si dimostri che la loro somma ha la stessa
area del triangolo.
Soluzioni 21/03/2012 classe 5C
1
Soluzioni
1) Considera le curve di equazione f ( x) =
kx 2 − k + 1
x2 +1
con k ∈ R
a) determina i punti comuni a tutte le curve
da y =
kx 2 − k + 1
1
1− x2
+
k
si
ricava
y
−
= 0 , le due generatrici del fascio sono:
x2 +1
x2 +1
1+ x2
1− x2
=0
1+ x2
1
y = x 2 + 1
tra le due generatrici
⇒
2
1 − x = 0
x 2 + 1
y=
1
se k = 0
2
x +1
se
e
k = ∞ , i punti comuni sono quindi i punti di intersezione
x = ±1
1
y = 2
b) determina k in modo che il grafico sia tangente alla curva di equazione y = 1 − 1 − x 2 nel suo
punto di minimo relativo; studia e rappresenta la funzione così ottenuta.
La curva y = 1 − 1 − x 2
ha un punto di minimo in P (0;0) , si tratta infatti di una
semicirconferenza con centro C(0; 1) e raggio R=1
y −1 = − 1− x2
1 − x 2 ≥ 0
y ≤ 1
2
2
x + ( y − 1) = 1
Poiché nel punto di minimo la derivata è nulla la condizione su f(x) è che passi per (0;0) e in
f ( 0) = 0
2kx( x 2 + 1) − 2 x(kx 2 − k + 1)
questo punto abbia derivata nulla
, calcolando y ' =
2
x2 +1
f ' ( 0) = 0
(
)
− k + 1 = 0
quindi k=1
0 = 0
La funzione è di conseguenza: f ( x) =
x2
x2 +1
D = (− ∞; + ∞ ) f (− x) = f ( x) pari
f ( x) =
x2
≥ 0 ∀x ( x = 0)
x2 +1
x2
∞
= F .I . ma
lim
2
∞
x →∞ x + 1
x2
x2
=
= 1 y=1 asintoto orizzontale
lim
lim
2
2
x→∞ x + 1
x →∞ x
Soluzioni 21/03/2012 classe 5C
2
f ' ( x) =
(x
2x
2
f ' ( x) ≥ 0
f ' ' ( x) =
)
D' = D
⇒
x≥0
+1
(
2
)
(x
x = 0 punto di minimo
2
2 x 2 + 1 − 8 x 2 ( x 2 + 1)
f ' ' ( x) ≥ 0
⇒ −
2
)
+1
1
3
4
=
(
(x
2 1 − 3x 2
2
)
+1
)
3
−
1
≤x≤
1
1
3
3
3
∩
1
x=±
punti di flesso y =
4
3
1
∪
∩
y
1
x
−1
1
c) Considera un punto P di ascissa positiva appartenente al grafico di f(x), calcola, in funzione
dell’ascissa del punto l’area del triangolo PHA, dove H indica la proiezione di P sull’asintoto e A è il
punto di coordinate (0;1). Determina quindi il punto P per cui risulta massima l’area del triangolo.
y
L’incognita più naturale è l’ascissa del punto P, con limitazioni
x ≥ 0.
A
x
, il punto H è invece
Il punto P ha quindi coordinate: x; 2
x +1
(x; 1) . Il triangolo PAH, rettangolo in H ha area
2
1
1
x2 1 x
=
A( x) = AH ⋅ PH = x1 − 2
, per determinare
2
2 x + 1 2 x 2 + 1
il punto di massimo si deriva e si studia il segno:
A' ( x) =
⇒
1− x2
(
)
2 x2 +1
2
H
1
P
x
1
2
≥0
−1 ≤ x ≤ 1
-1
Soluzioni 21/03/2012 classe 5C
0
1
3
x=1 punto di massimo
1
Il punto P per il quale è massima l’area del triangolo APH ha coordinate 1;
2
2) Un settore circolare di raggio 2 è lo sviluppo della superficie laterale di un cono. Determina l’ampiezza
dell’angolo al centro del settore in modo che il cono abbia volume massimo.
Etra le diverse possibili incognite, è più comodo
scegliere x = OV , cioè l’altezza del cono, le
limitazioni sono: 0 < x < 2 e il raggio del cono,
V
dal teorema di Pitagora è: OA = 4 − x 2 .
B
V
A=B
O
La funzione volume, da ottimizzare è quindi, in
funzione di x data da :
A
V ( x) =
2
1
1
1
πOA ⋅ OV = πx(4 − x 2 ) = π(4 x − x 3 )
3
3
3
per
determinare il massimo, basta derivare
1
2
2
V ' ( x ) = π( 4 − 3 x 2 ) ≥ 0 ⇒ −
≤x≤
3
3
3
x=
2
3
e
studiare
−
il
2
3
segno
della
0
derivata:
2
3
punto di massimo, il raggio di base del cono è
quindi OA = 2
2
3
Considerando lo sviluppo del cono, l’angolo del settore circolare è, per definizione di angolo in
arco( AB ) 2πOA
radianti: α =
=
=
VA
VA
4π
2
2
3
= 2π
2
≈ 294°
3
3) Su un cartoncino rettangolare si deve applicare una fotografia di 300 cm2 con il margine
superiore e inferiore di 3 cm e con i margini laterali di 4 cm. Che
D
dimensione deve avere il cartone di area minima che serve allo scopo?
Indicando con x la base della fotografia si avrà x > 0 e, essendo 300
300
cm2l’area della fotografia, l’altezza sarà H =
.
x
300 cm2
3 cm
A
Soluzioni 21/03/2012 classe 5C
C
x
4 cm
B
4
300
300
+ 6 e quindi l’area A( x) = ( x + 8)
+ 6 ;
x
x
per determinare il minimo della funzione, si calcola la derivata e se ne studia il segno:
300
300
A' ( x) =
+ 6 + ( x + 8) − 2
x
x
Le dimensioni del cartone sono: AB = x + 8
A' ( x) = 6 −
2400
6 x 2 − 2400
≥
0
≥0
x2
x2
BC =
⇒
x ≤ −20 ∨ x ≥ 20
20
x=20 punto di minimo. Le dimensioni del cartoncino sono quindi:
AB = x + 8 = 28 cm
BC =
300
+ 6 = 21 cm .
x
4) Dopo aver enunciato il teorema delle tre perpendicolari, si calcoli la superficie laterale della
piramide ABCV così caratterizzata: la base è il triangolo rettangolo ABC retto in C avente AC = 3a
)
π
e CAB = , altezza VH = a che incontra il lato AC in H con HC = a .
3
r
P
s
α
Il teorema delle tre perpendicolari dice che dato un piano
una retta r ad esso perpendicolare in P,
ed
una retta s giacente sul piano, è perpendicolare al piano
individuato da r e dalla normale ad s passante per P.
Le misure dei lati sono: AB = 6a , BC = 3a 3 .
La faccia laterale ACV ha come base AC ed altezza HV, quindi la sua area è:
Area ( ACV ) =
AC
3
⋅ HV = a 2 .
2
2
B
V
6a
3a 3
C
H
K
Soluzioni 21/03/2012 classe 5C
C H=V 3a
A
A
K
B
5
2
La faccia laterale BCV ha come base BC ed altezza VC = HC + HV
Area ( BCV ) =
2
= a 2 , quindi la sua area è:
BC
3 6 2
⋅ CV =
a .
2
2
2
La faccia laterale ABV ha come base AB ed altezza VK = KV + HV
HA = 2a quindi KH = a 3 )quindi la sua area è: Area ( ABV ) =
2
= 2a ,(osservando che
AB
⋅ KV = 6a 2 .
2
3 3 6
15 + 3 6 2
La superficie laterale è quindi: Area = ( +
+ 6) a 2 =
a
2
2
2
5) Dato un triangolo rettangolo inscritto in un semicerchio, se sui suoi cateti presi come diametri ed
esternamente si costruiscono due semicerchi, da questi e dal dato semicerchio sono determinati due
menischi, dette lunule di Ippocrate. Si dimostri che la loro somma ha la stessa area del triangolo.
L’area dei sue menischi si può ottenere sottraendo dalla
somma delle area dei due semicerchi che hanno per diametro i
cateti la differenza tra l’area del semicerchio che ha per
diametro l’ipotenusa e l’area del triangolo. Dette a, b, c i lati
del triangolo si ha:
b
c
a
2
2
2
π
b
c a
A(lunule) = π + π − π − A(triangolo) = (b 2 + c 2 − a 2 ) + A(triangolo)
4
2
2 2
Per il Teorema di Pitagora a 2 = b 2 + c 2 cioè b 2 + c 2 − a 2 = 0 , quindi, sostituendo nell’uguaglianza
precedente: A(lunule) = A(triangolo)
Soluzioni 21/03/2012 classe 5C
6