Nucleosintesi sul sole

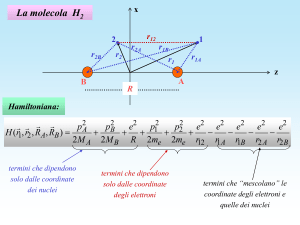
Stelle e Radioattivita’
Processi nucleari governati da interazioni debole, forte ed
elettromagnetica responsabili della produzione di energia e materia
sulle stelle.
Ruolo fondamentale della gravita’.
Modelli teorici per descrivere e interpretare la produzione di
energia: caso particolare del sole (Solar Standard Model- SSM).
Luminosita’ del sole (=potenza irradiata).
Catena PP e ciclo CNO: ruolo del deuterio e delle teorie di Fermi
e Dirac.
Calcolo della luminosita’ del sole.
Cenni di nucleosintesi. Problema della materia organica e dei
nuclei pesanti.
Fase terminale nel ciclo stellare: supernova SN1987A e limite
Superiore a massa neutrino.
Eta’ dell’ Universo
Il Sole
►sfera di gas perfetto costituita da plasma di protoni, particelle a
ed elettroni.
►condizioni di equilibrio fra compressione gravitazionale ed
espansione termica
►calore sviluppato in una regione centrale di raggio ~ (1/4)
del raggio solare, si propaga all’esterno per convezione e radiazione.
►potenza irradiata è mediamente costante nel tempo
►temperatura, pressione e densità crescono dalla periferia al centro
Distribuzione energetica della radiazione solare a livello del suolo e al di
fuori dell’atmosfera (confrontata con la radiazione di corpo nero alla
temperatura di ~ 5770 °K). I minimi nella distribuzione energetica al
suolo corrispondono a lunghezze d’onda di assorbimento da parte di
molecole di ozono, ossigeno acqua e anidride carbonica presenti
nell’atmosfera.
Tabella 1. Parametri solari. Le quantità in corsivo sono misurate, le altre calcolate dai modelli solari. (Cremonesi, Galeotti)
__________________________________________________________________
Raggio
R = 6.96 105 km
Massa (~ 3.33 105 masse terrestri)
M =1.99 1033 g
Distanza terra-sole
d = 1.49 108 km
Luminosità (potenza irradiata)
L = 3.856 1033 erg s–1
= 2.41 1039 MeV s–1
= 9.22 1025 cal s–1
= 3.856 1026 Watt
Luminosità dei neutrini
0.023 L
Flusso medio di radiazione sulla terra per
unità di superficie all’esterno dell’atmosfera 1.36 106 ergcm–2 s–1
1.95 cal cm–2 min–1
8.5 1011 MeV cm–2 s–1
1.36 103 Wat·m-2
Temperatura al centro
1.56 107 oK
alla periferia
5.78 103 oK
Pressione al centro
2.5 106 atm.
alla periferia
0
Densità al centro
158 g cm–3
alla periferia
0
Densità media
1.409 g cm–3
Età
4.55 109 anni
Abbondanza iniziale di elio in massa
27%
Abbondanza iniziale di elementi pesanti 2%
Abbondanza di idrogeno al centro
34%
Flusso di neutrini dalla catena pp
6 1010 cm–2 s–1
Flusso di neutrini dal 8B
6 106 cm–2 s–1
Frazione di energia dalla catena pp
98.4%
Frazione di energia dal ciclo CNO
1.6%
__________________________________________________________________
►maggior parte delle informazioni sulla struttura del sole dalla
radiazione elettromagnetica prodotta sotto forma di fotoni nella regione
centrale del sole
raggiunge (in un tempo stimato di 10 6 anni o più!!) la superficie tramite
una successione di atti di assorbimento ed emissione che ne degrada
progressivamente l’energia.
informazioni sulla regione interna del sole trasportate dalla radiazione
elettromagnetica profondamente alterate dai processi di trasmissione
►2 % dell’energia liberata emessa sotto forma di neutrini.
elevata probabilità di emergere senza interagire con la materia solare
mantengono inalterate le caratteristiche originarie
ma bassa probabilità di interazione dei neutrini
Origine dell’energia solare
varie ipotesi
Ipotesi chimica
►Esempio: combustione del carbone
C  O 2  CO 2
Ipotesi: massa solare costituita da 1/3 di carbone e da 2/3 di ossigeno
Combustione di 1 g di carbone produce 8 103 calorie = 3.35 1011 erg,
E = (energia/grammo) x massa sole =
= (1/3) 3.35 1011 erg/g 1.99 1033 g = 2.22 1044 erg
► Durata del sole = Energia/Luminosità
E(erg)
2.22 10 44 erg
t

 0.57 1011 s  1.8 103 a
33
L(erg / s) 3.861 10 erg / s
valore troppo piccolo
►dallo studio delle rocce età del sole ≈ 109 anni
Ipotesi gravitazionale
►Ipotesi: materia solare inizialmente costituita da frammenti di massa dm a
distanza infinita, i frammenti si raccolgono per attrazione gravitazionale in un
volume sferico di raggio R l’energia gravitazionale diminuisce trasformandosi (in
parte) in energia cinetica dei frammenti
►calcolo della diminuzione di energia potenziale una quantità di massa m di
materia solare si sia già raccolta con simmetria sferica entro una sfera di raggio r <
R variazione di energia relativa a un ulteriore accumulo di materia in uno strato
infinitesimo di spessore dr è
r
 4r 2 dr
mdm
2
dV  G
 G  4r dr 
r
r
0

 = (r) = densità della materia solare
►variazione totale approssimata: r = costante = valor medio
  m 
V   0
R
M
4
R 3
3
(4) 2 2 R 5
3 M2
dV  G
m
 G
3
5
5 R
V = (3/5) 6.6 10-8 cgs (2 1033 g)2/ (7 1010 cm)
= –2.26 1048 erg = -1.41 1054 MeV
durata del sole
V
2.26 10 48 erg
t

 5.8 1014 s  1.8 10 7 anni
33
1
L
3.86 10 erg  s
Valore troppo piccolo
Fusione nucleare
Energia di legame per nucleone B/A in funzione di A per i nuclei stabili.
►Fusione di nuclei leggeri → nuclei più pesanti con A≤56 e liberazione di energia
2
2
2
Q  M(A1)c  M(A2 )c  M(A3  A1  A2)c 
 A1(B3  B1)  A2 (B3  B2 )  0
Fusione ostacolata dalla barriera repulsiva coulombiana
Probabilità di fusione aumenta con l’energia cinetica dei nuclei in collisione
aumenta con la temperatura del gas solare
Ciclo pp
p  p  e  d  
p  p  d  e  
99.75%
0.25%
d  p3 He  
14 %
0.02%
3
hep
He  p  e     4 H
H ee
ee
ee
ee
3
He  4 He  7Be  
99.98 %
7
Be  e  7Li  
0.02 %
7
Be  p  8B  
8
B 8 Be  e   
86 %
3
He  3He  4 He  p  p
7
Li  p 4 He 4 He
8
Be 4 He 4 He
pp 1
pp 2
pp 3
———————————————————————————
Ciclo CNO
12
C  p
13
N
15N  p    12 C
15
13N  e    13C
13
C  p
14
N
15
4
16
O p 
O  e     15 N
17
F  e    17O
14
17
N  p
N  p
CNO
16
4  10
15
O
O
17
F
O  p  
14
N
Energia liberata nella diramazion e pp1.
Energia liberata
p  p  d  e  
2m p  m d  me 
 m p  m n  Bd  me
e +  e   2
 2me
d  p  3 He  
m p  md  m( 3 He) 
0.42 MeV
 1.02 MeV
 B 3 He  Bd
3
5.49 MeV
He  3 He 
 4 He  2 p
2m( 3 He)  2m p  m( 4 He)
 B ( 4 He)  2 B ( 3He)
 12.86 MeV
Energia totale liberata per formare un nucleo di 4 He =
= 2(0.42 + 1.02 + 5.49) + 12.86 = 26.72 M eV
Energia media trasportata dai 2 neutrini
 0.52 MeV
►Fusione fondamentale sul sole pp→d
Seguita da successione di reazioni sintetizzabili in
M(6p)c2→M(4He)c2+M(2p)c2+ 26.72 MeV
Probabilità significativa per T ≈ 10 7 °K
Al crescere della temperatura, diramazioni pp2 e pp3 tendono a
prevalere su pp1
se l’abbondanza di 4He è sufficientemente elevata,
la cattura elettronica del 7Be in pp2 tende ad avere la stessa
importanza della cattura del protone da parte del 7Be in pp3.
Tutte le diramazioni terminano con la produzione di 4He.
Velocità di produzione di deuterio nella catena pp
probabilità per unità di tempo che si verifichi la reazione
p  p  d  e  
determinata
(i)dalla probabilità per unità di tempo che nella collisione pp un protone
si trasformi in neutrone e si formi un deutone
(ii) dalla probabilità che venga superata la barriera repulsiva coulombiana,
(iii) dalla temperatura media della regione centrale del sole,
(iv) dalla distribuzione maxwelliana dell’energia dei protoni
(v) dalla densità di protoni,
Formazione del deutone (trascurando la repulsione coulombiana)
due protoni a distanza nucleare (~ 10 –13 cm)
p  p  d  e  
stato iniziale → legame nucleare “debole” (non esiste stato legato stabile fra
due protoni)
principio di esclusione di Pauli → funzione d’onda per due fermioni identici
antisimmetrica nelle coordinate spaziali e spinoriali
energia cinetica piccola → due protoni in onda S
(momento angolare orbitale L = 0)
funzione d’onda spaziale simmetrica,
parità P = (1) L
0
spin ½ + ½ →
Funzione d’onda antisimmetrica
1
Funzione d’onda simmetrica
stato finale → protone e neutrone legati nel deutone
deuton
e
spin
1
momento angolare orbitale
L =
0
Implicazioni: variazione dello spin 0 → 1 dei due nucleoni
p legato  n legato  e   
per interazione debole con interazione di Gamow-Teller
Densità di probabilità di transizione per unità di tempo
p  p  d  e  
►
dw 2
d N
2

H if
dp e

dE 0 dp e
2
H if   f* Hi dvdv e dv 
H  g GT (re  r)(r  r)
gGT = costante di accoppiamento di Gamow-Teller
r = coordinata del nucleone che decade
►Trascurando l’interazione coulombiana fra positrone e deutone
e 
1 ik e re
e

 
1 ik  r
e

  *  d  1
.
Per
k r
<< 1
e   
1

Coppia elettrone-neutrino in onda S rispetto al nucleo finale (momento angolare orbitale = zero)
►coppia pp in moto libero nello stato S
 pp 
1 sen kr
1

 kr

k = p/

, p = impulso del moto relativo
►deutone (solo contributo in onda S in approssimazione
di “ raggio d’azione nullo”)
2K d e  K d r
d 
4 r
1/Kd = 4.3 fm = “raggio del deutone”
H if
2
g
 3/ 2



0
2
2K d e
g 2 8
dv  3 3
4 r
 Kd
Kd r
►
dw 2
d2N
2

H if
dp e

dE 0 dp e
2
H if
2
g
 3/ 2



0
2K d e  K d r
g 2 8
dv  3 3
4 r
 Kd

d 2N
4  ( E0  Ee ) 2  pe c 

dE0 dpe 2 6
c3
c2
2
2
E 0  2m p c 2  m d c 2
.
2
2
dw 2  g 2 8  4  Eo  Ee  2 
 3 3 

pe 
dpe
   K d  2 6
c3

►
w   dpe
dw
dpe
dpe
integrabile numericamente
integrazione approssimata se Eo » mec2
→
E o2  p e2 c 2  m 2e c 4  p e2 c 2
w  0
po
po
dw
1
4g 2
2 2
dp e 
(
E

E
)
p e dp e ~
o
e

dp e
  2 K 3d  7 c 3 0
1
4g 2
~
  2 K 3d  7 c 6

Eo
0
E 5o
1
4g 2
(E o  E e ) E dE e 
  2 K 3d  7 c 6 30
2
2
e
probabilità per unità di tempo che due protoni in un volume  , una volta incontratisi
a distanza nucleare dopo aver superato la barriera coulombiana, fondano in un deutone
g  g GT ~ 1.7910 49 erg  cm3  1.1210 43 MeVcm3
K d  2.321012 cm1
E o  0.93MeV
  6.5810 22 MeV  s
w ≈ (1/W) 2.4 10–40 s–1
(valore più accurato w =(1/W) 1 × 10–40 s–1)
Trasparenza della barriera coulombiana
avvicinamento dei protoni a distanza nucleare ostacolato dalla repulsione colombiana
probabilità di superare la barriera repulsiva cresce con energia cinetica
energia cinetica fornita inizialmente dall’energia termica accumulatasi nella fase di contrazione gravitazionale
contrazione gravitazionale →
aumento progressivo della temperatura del gas →
innesco dei processidi fusione nucleare→
emissione di energia →
espansione del gas solare →
bilanciamento della compressione gravitazionale →
situazione di equilibrio durante il quale il sole mantiene un volume
costante ed emette energia con potenza costante.
Barriera colombiana
zZ4.8 10 10 
zZe 2
B

MeV
R
R (fm) 10 13  1.6 10 6
2
energia cinetica media
3
E  kT
2
k = 1.36 10–16 erg/grado (costante di Boltzmann)
►trasparenza della barriera per energia cinetica del moto relativo piccola
  e    10 0.43
  2
zZ
zZ
m

 2
c

137
137 2E
E
►Valutazioni numeriche per il moto di un protone di energia E contro un protone fermo.
La velocità v è quella di una particella di massa ridotta m = m/2 v = (2E/m) 1/2.
_________________________________ _____________________________________
R pp  ~ 2fm
B  0.72 MeV
TK 
107
1.5 107
108
300
3
E(MeV)  KT
2
1.29 10 – 3
1.94 10 – 3
1.29 10 2
3.88 10 8
–3
2.03 10 – 3
10 9.7
5.24 10 – 3
10 3.76
8.27 10 –7
β
τ
1.65 10
~ 10 –12
~0
__________________________________________________________________________
►energia cinetica effettiva distribuita attorno alla media secondo la
distribuzione di Maxwell
2
f (E)dE 
 kT 
Ee
3/ 2

E
KT
dE
trasparenza della barriera coulombiana più grande o più piccola di quella corrispondente all’energia media
►valore della trasparenza mediato sulla distribuzione di Maxwell


   E  
2
2
kT 

   (E)f (E)dE 
E
e
dE


 (kT) 3 / 2
 (kT) 3 / 2
E


>>  (Emedia )
~ 105  ~ 10–9.7 x 10 5 ~ 2 10 5
grande incremento perchè la trasparenza della
barriera coulombiana è funzione rapidamente
crescente dell’energia
frazione consistente di particelle con energia
superiore alla media
E m ax
 kT 


 2 
2/3
3
 kT
2

Ee
  E 

 
 E kT 
dE
Luminosità del sole
►dNd/dt = numero di deutoni prodotti nell’unità di tempo nelle collisioni fra N
protoni in un volume 
 = (4/3)  (1/4 Rsolare )3 ~ 0.22 1032 cm3
alla temperatura
T=1.5 10 7 K
dN d
 probabilit à che 1 coppia di p in un volume  formi un deutone 
dt
numero n pp di coppie di p in   w    n pp
►
w    2.4 10 40 s 1  2 10 5  2 10 
45
► npp = numero combinazioni p a due = N(N–1)/2 ~ N2/2
numero di coppie di protoni equivale a numero di collisioni protone-protone
► N = numero protoni nel volume  = (densità p) × 
densità materia solare
100 g  cm3
 np 
 6.25 10 25 p / cm3
 24
massa p
1.6 10 g
57
N  n p   1.38 10
densità p 
►
dN d 1.24 2 10114

 2 10  45  0.86 10 38 s 1
32
dt
2  0.2  10
►Produzione di 1 nucleo di 4He ogni due deutoni con liberazione di 26.72 MeV
dN He 1 dN d

 0.43 10 38 s 1
dt
2 dt
Luminosità del sole calcolata
valore sperimentale
L = 26.72 ·(dNHe /dt) = 1.15 10 39 MeV/s
2.4 1039 MeV/s
vita del sole
Ipotesi: tutto l’idrogeno del sole contribuisce alla formazione di 4He
energia totale liberata
M sole 4
2 10 33 g
E
E( He ) 
 26.72 MeV  8 10 57 MeV
 24
4m p
4  1.67 10 g
durata del sole
E
8 1057 MeV
t

 3.3 1018 s  100 109 a
39
Lu min osità 2.4 10 MeV / s
età oltre 20 volte l’età attuale del sole
In realtà ci si attende che solo 1/10 circa dell’idrogeno dia origine a 4He
perchè la temperatura delle regione esterna del sole ha temperatura troppo bassa
e la struttura del sole cambia notevolmente quando l’idrogeno della regione centrale
è prossimo all’esaurimento.
Pertanto la durata del sole si riduce a circa 10 miliardi di anni, il doppio dell’età attuale.
Cenni di nucleosintesi
Da gas di soli protoni nascono deutoni, 3He, 4He ecc.
formazione di nuclei più pesanti per fusione di nuclei più leggeri
nucleosintesi
sole e stelle laboratori per la creazione di nuclei atomici.
evoluzione delle stelle
composizione delle stelle è in continua evoluzione
diminuzione dei nuclei leggeri e aumento di nuclei via via più pesanti
evoluzione stellare mediante processi iterativi
contrazione gravitazionale
aumento della temperatura
innesco dei processi di fusione pp quando la regione centrale aggiunge ≈107 °K
fusione di idrogeno in d, 3He, 4He (7Li, 7,8Be, 8B)
esaurimento dell’idrogeno nella regione centrale
cessa la produzione di energia da fusione
la temperatura diminuisce
la pressione gravitazionale contrae la stella
aumenta nuovamente la temperatura
a ≈ 108 °K fusione di nuclei di 4He →
4
He  4 He 8 Be
4
He  8 Be12 C  
4
He 12 C16 O  
3) esaurito l'4He
 stelle di piccola massa (sole): processi di fusione cessano,
la stella perde luminosità
♣ stelle di grande massa
si ripete la successione di processi in (2)
a ≈ 109 °K si innescano fusioni di 14C
e così via finchè il nucleo del sole si arricchisce di nuclei con A = 56 (Fe, Ni)
e i processi di fusione hanno termine
la contrazione gravitazionale non più contrastata dalla pressione termica e,
dipendentemente dalla massa della stella, possono intervenire fenomeni catastrofici
che in tempi brevi causano l’esplosione della stella.
Processi con nuclei pesanti: fusione dell’ elio
Fusione dell'elio: Questa reazione di fusione nucleare può avvenire solo in
ambienti che siano ricchi di elio, sottoposti a pressioni elevate e a temperature
superiori a 100.000.000 gradi.
il processo alfa
12C
+ 4He
→
16O
16O
+ 4He
→
20Ne
+γ
→
24Mg
+γ
20Ne
+ 4He
+γ
il processo tre alfa
+ 4He ↔ 8Be
8Be + 4He ↔ 12C + γ + 7.367 MeV
4He
Processi con nuclei pesanti: fusione del carbonio
Il processo di fusione del carbonio è una reazione di fusione nucleare che
avviene nelle stelle massicce (almeno 4 volte la MSole alla nascita) quando
hanno esaurito tutti gli elementi più leggeri nel loro nucleo.
Richiede elevate temperature (6×108 K)
12C
+ 12C
→
24Mg
+γ
→
23Mg
+n
→
23Na
+ 1H
→
20Ne
+ 4He
→
16O
+ 24He
Processi con nuclei pesanti: fusione del neon
Il processo di fusione del neon è un insieme di reazioni di fusione nucleare
basate sul Neon che avvengono in stelle massicce (almeno 8 MSole).
La fusione del Neon richiede alta temperatura (circa 1.2×109 K ).
A temperature così alte la fotodisintegrazione è importante, e così
alcuni nuclei di Neon si decompongono rilasciando particelle alfa
20Ne + γ → 16O + 4He
Queste particelle alfa possono essere riutilizzate per produrre magnesio-24
20Ne + 4He → 24Mg + γ
In alternativa
20Ne + n → 21Ne + γ
21Ne + 4He → 24Mg + n
dove il neutrone prodotto nel secondo passo può essere riutilizzato nel primo.
Processi con nuclei pesanti: fusione dell’ ossigeno
Il processo di fusione dell'ossigeno è una reazione di fusione nucleare
che avviene in una stella massiccia quando questa ha esaurito gli elementi
più leggeri nel proprio nucleo. La fusione avviene alla temperatura di 1.5×109K
Tutte le reazioni seguenti possono avvenire, anche se la più probabile è quella
che produce il Silicio.
16O
+ 16O
→
32S
+γ
16O
+ 16O
→
31S
+n
16O
+ 16O
→
31P
+ 1H
16O
+ 16O
→
28Si
16O
+ 16O
→
24Mg
+ 4He
+ 24He
Processi con nuclei pesanti: fusione del silicio
Il processo di fusione del silicio è una reazione di fusione nucleare
che avviene nelle stelle massicce. Richiede temperature di 2.7×109 K
Le reazioni che avvengono sono le seguenti:
28Si
+ 28Si
56Ni
56Co
→
→
→
56Ni
+γ
56Co
+ e+ +
νe
56Fe
+ e+ +
νe
Il processo di fusione del silicio è estremamente rapido; una stella
mediamente brucia il silicio accumulato nelle fasi precedenti in un solo
giorno. Questo è anche l'ultimo passo nella vita di una stella, in quanto il
prodotto finale, il Ferro-56, è uno degli isotopi più stabili dell'Universo.
La fusione non può procedere ulteriormente, se non tramite processi
endotermici (quali la cattura di neutroni, vedi processo-r, processo-s), che
richiedono per avvenire più energia di quanta ne producano.
Il nucleo della stella non può produrre più energia e quindi si raffredda.
Allora la contrazione gravitazionale non è più compensata dalla produzione
di energia e il collasso della stella è inevitabile. Questo termina con
l'esplosione di una supernova e la formazione di una stella di neutroni (o anche
di un buco nero, se la stella è sufficientemente massiccia).
La supernova rilascia una enorme quantità di energia che rende possibile la
formazione di nuclei più pesanti del Ferro tramite il processo di cattura rapida
di neutroni (il processo-r).
Nuclei presenti sul sole e loro origine
Analisi dello spettro di radiazione emesso dalla superficie solare
Abbondanze degli elementi nel sole in funzione del numero atomico A. La distribuzione è normalizzata
ponendo uguale a 10 6 l’abbondanza del silicio. Sono messi in evidenza gli elementi con numeri magici di
neutroni (N=50, 82, 126). I nuclei da He a Ca hanno A=4n, n=1, 2, 3, .
sul sole sono presenti tutti gli elementi esistenti sulla terra
ma solo nuclei leggeri con A<16 sono prodotti dai processi di fusione nel nocciolo del nuclei più pesanti prodotti
da altri processi
abbondanza degli elementi è caratterizzata da picchi e gobbe, che riflettono particolari modalità di formazione
dei nuclei
origine dei nuclei con A< 56
a) il sole ha avuto origine verosimilmente dall’esplosione di una stella di
grande massa in
cui erano presenti nuclei con A< 56
a) l’abbondanza decresce al crescere di A:
i) fusione nel sole incrementa nuclei con A < 16;
ii) la repulsione coulombiana ostacola la produzione di nuclei al crescere di Z
a) picchi per A < 16 riflettono la particolare stabilità dei nuclei con A multiplo di 4
a) Picco del Fe: il ferro è elemento di accumulazione per i processi
di fusione dei nuclei più leggeri e non è soggetto a fusione.
Nucleosintesi e materia organica
sezione d’urto d’interazione di due nuclei → valori elevati per energia di collisione con produzione
di nuclei in livelli eccitati
sezione d’urto risonante.
12C costituente fondamentale della materia organica con azoto e ossigeno
3
7.275 MeV
 + 8 Be
7.654 MeV
4.439 MeV
7.366 MeV

12 C
2 10 16 s
    92 keV 8 Be  2
Piccola probabilità di fusione in carbonio eccitato
8
Be  12 C * 12 C  7.654MeV
7.6547.275 MeV  379 keV energia termica necessaria per produrre C*
da 3  T ~2 10 8 °K
Decadimenti 12C*→3 prevalente
C*→12C + n
0.04%
sufficiente per spiegare l’abbondanza di C osservata nell’universo
12
12C
+  →16O
formazione di nuclei con A > 56
►assorbimento di neutroni da parte di nuclei stabili con A < 56 produce
nuclei con eccesso di neutroni che decadono   in isobari stabili con A crescente
nucleo stabile (Z, N) cattura neutroni, diviene instabile, decade – , diviene un nucleo con Z´=Z+1;
questo, a sua volta, assorbe neutroni finché non diventa instabile, decade –, si trasforma in un nucleo
con Z˝=Z+2 e così via.
►assorbimento poco probabile per nuclei magici
Effetti diversi per flussi di neutroni di bassa e alta intensità
a) Bassa intensità (processi s): la probabilità di assorbimento di 1 neutrone è più piccola della probabilità
del conseguente decadimento –.
Neutroni prodotti da reazioni secondarie nel sole
14
7
N  189 F  
18
9
F188 O  e   
18
8
O  22
Ne 
10
22
10
25
Ne  12
Mg  n
I nuclei assorbitori aumentano A di una unità prima di decadere
1 g di materia solare produce 1021 neutroni, quantità sufficiente per spiegare le abbondanze osservate
a)Elevata intensità (processi r): i nuclei stabili possono assorbire più di un neutrone prima di decadere  
Neutroni prodotti nella fase di collasso di stelle di grande massa
I nuclei assorbitori possono subire una “grande” variazione di A allontanandosi molto dalla linea di stabilità
prima di decadere
c) I nuclei magici sono nuclei di accumulazione dei nuclei
non magici più leggeri e sono scarsamente coinvolti
dall’assorbimento di neutroni. La loro accumulazione ha
un ritmo più elevato della loro riduzione.
d) abbondanza dei nuclei sul Sole ha portato a
individuare la presenza di nuclei pesanti prevalentemente
prodotti da processi s ( Ba, La, Cs e Pb) e nuclei
prevalentemente prodotti da processi r (Eu, Gd, Dy, Th e
U).
►assorbimento di protoni dà origine a nuclei ricchi di
protoni non producibili mediante i processi s e r; i
meccanismi principali sono reazioni di cattura del tipo
(p,) e (p,n)
Contributo dei processi r alla produzione
di nuclei sul Sole.
Sono indicati con i nomi degli elementi quelli
per i quali il contributo è superiore al 70%
o inferiore al 30%.
Collasso della supernova SN1987A
limite superiore della massa del neutrino
►stella di grande massa (> 3 volte massa del sole) con nocciolo centrale
trasformato in ammasso di nuclei di Fe e Ni,
subisce processo catastrofico con esplosione dello strato esterno
e implosione del suo nocciolo → stella di neutroni o in un buco nero
►fenomeni associati previsti:
temporaneo aumento della luminosità della stella, (miliardi di volte quella del sole)
emissione di neutrini elettronici
e  p  n  e
emissione coppie neutrino-antineutrino
e  e    
Emissione in pochi secondi di energia gravitazionale tramite un flusso di
circa 10 58 neutrini di energia dell’ordine di 10-20 MeV.
23 e 24 febbraio 1987
Osservazione eventi compatibili con le reazioni
e  e  e  e
e  p  n  e 
24 febbraio 1987, 5h 31m 12s
bagliore proveniente dalla Grande Nebulosa di Magellano
esplosione supernova SN1987A
►storicamente documentate negli ultimi due mila anni nella nostra Galassia solo 8 supernove prima della SN1987A
l’ultima nel 1604!
limite superiore della massa del neutrino elettronico.
►sezioni d’urto
2g 2F m e c 2
( e e ) 
E   1.65 10 44 E  cm2
4
(c)

g2
( e p) 
E 2  1.65 1044 E 2 cm2
4
(c)
a parità di energia valore più elevato
►Dalla misura dell’energia dell’elettrone
energia del neutrino
E   m n  Tn  E e  m p  m n  E e  m p  1.29  E e MeV
►ipotesi relative alla distribuzione temporale degli eventi
a) m = 0 → l v = c (indipendentemente dall’energia)
→ distribuzione temporale degli eventi osservata sulla Terra = distribuzione dei neutrini
al momento dell’emissione dalla stella.
b)
m  0
e neutrini emessi simultaneamente → arrivano sulla terra prima i più energetici e dopo i meno energetici
c)
m  0
e neutrini emessi dalla stella casualmente entro t →
distribuzione temporale sulla terra non ordinata corrispondentemente
alla distribuzione energetica in un intervallo di tempo
t 
più lungo o più corto di t
► Distribuzione temporale ed energetica dei primi 8 eventi osservati con il rivelatore Kamiocande II
_________________________________________________________________________________________
T (s)
Ee
(MeV)
1
2
3
4
5
6
7
8
0.
0.107
0.30
3
0.32
4
0.50
7
1.54
1
1.728
1.91
5
20.0
±2.9
13.5
±3.2
7.5
±2.0
9.2
±2.7
12.8
±2.9
35.4
±8.0
21.0
±4.2
19.8
±3.2
E(MeV
21.3
14.8
8.8 10.5 14.1 36.7
22.3 21.1
__________________________________________________________________________________
) neutrini meno energetici sono arrivati prima di neutrini più energetici
ipotesi verosimili
a) m = 0 (distribuzione temporale sulla stella = sulla terra)
c)
m  0
e neutrini emessi dalla stella casualmente entro t
► relazione
fra t e  t
Distanza Supernova-Terra
L  1.5 10 5 anni luce  1.5 10 5  3600  24  365  c (cm / s ) cm
 c  4.73 1012 cm
Tempo di percorrenza per neutrini con massa = 0, v = c
t
= L/c ~ 4.73 1012 s ~ 1.5 105 a
Supernova esplosa 150.000 anni fa !!!!
Tempo di percorrenza per massa ≠ 0,
2
m 
v  c 1    
 E 
L L
1
t m  
v c
m
1   
 E
2
L  1  m  
 
 1  
2
c
2
E

   



t = istante di emissione,
t   t  t m
t   t  t m
t’ = istante d’arrivo
intervallo di tempo fra l’arrivo di due neutrini i e j
t i  t j  (t i  t j )  (t mi  t mj )
corrispondente intervallo di tempo all’emissione
t i  t j  ( t i  t j ) 
L 2  1
1 
m   2  2  
2c  E i E j 


1
1
s
 ( t i  t j )  2.36 m 2 (eV) 2
 2

E
(
MeV
)
E
(
MeV
)
j
 i

►Se
E i  E vj
e
t i  t j  0
(il neutrino più energetico giunge sulla terra dopo il neutrino meno energetico) →
t i  t j  t i  t j
(intervallo di tempo sulla stella > di quello sulla terra).
Per i = 6, Emax = 36.7 MeV
j = 3, Emin = 8.8 MeV
t 6  t 3  1.238  0.029m 2 s
Ipotesi:
t6  t3
< t prefissato < 2 × valore osservato sulla terra ≈ 4 s
m 2  0.029
t  1.238
0.029
___________________________________________________________________________________
m (eV)
t (s)
m   10eV
0
6
≤ 1.238 2.282
8
3094
10
12
16
4.138
5.41
48.66
(include il valore zero)
Altra stima del limite superiore della massa del neutrino
►limite superiore dedotto dall’energia del primo neutrino rivelato dall’apparato
sotto il Monte Bianco (7 ± 1.4 MeV) e dal ritardo fra la sua rivelazione e quella del
segnale dell’antenna per onde gravitazionali (t=1.4±0.5 s)
velocità onda gravitazionale = c
tutto il ritardo dovuto a v < c, ossia alla massa del neutrino
m  (eV)
L L
t  t m  t    2.36
v c
E  (MeV )2
2
m   4.5eV
Limite inferiore dell’Età delle stelle e dell’Universo
Sul Sole e sulle stelle presenza di tutti i nuclei stabili e di nuclei a lunga vita media
quali l'uranio e il torio con circa la stessa abbondanza → processi di formazione simili su sole e stelle
Tuttavia la presenza di un nucleo particolare è riconoscibile nello studio dello spettro luminoso
d'emissione solo se la sua abbondanza è sufficientemente elevata e la stella sufficientemente vicina
solo su alcune stelle osservata la presenza di nuclei radioattivi a vita media lunga
nuclei prodotti in processi r sono presenti con abbondanze immutate nel tempo se stabili, decrescenti se
instabili
►abbondanza residua al tempo t di torio (prodotto in modo impulsivo dall’esplosione di una supernova
con processo r al tempo t' = 0)
n Th (t )  n(0)e  Tht
X = nucleo stabile prodotto in processo r
n Th ( t ) n Th (0) Th t

e
n X ( t ) n X (0)
t
1
Th
ln
nX (t ) nTh (0)
1
 2.3
nTh (t ) nX (0)
Th

nTh (0)
n (t ) 
 log10 Th 
log10
nX (0)
nX (t ) 

nTh (t ) / nX (t )
= rapporto fra le abbondanze misurato oggi
nTh (0) / nX (0)
????
Ipotesi verosimile: all’origine
 n X (0) 
 n (0) 

   X 
 n Y (0)  sole  n Y (0)  stella
 n Th ( t s )  Thts
 n Th (0) 
 n Th (0) 


 n (t )  e
 n (0) 
 n (0) 
 X
 stella  X
 sole  X s  sole
n Th (t s ) / n X (t s )
= rapporto odierno sul sole
età del sole è nota (ts = 4.5 109 a)
. Abbondanze relative attuali e all’origine sul Sole e attuali sulle stelle.
Nella penultima colonna sono riportate le corrispondenti età e, nell’ultima riga, la loro media pesata.
In particolare sono state studiate due stelle nella Via Lattea
CS22892-052 e CS31082-001, situate nella zona periferica a cui
appartengono le stelle piu’ antiche della Galassia.
Log10R(ts )
Log10
R(0)
Log10R(t)
Età (109 a)
232Th/Eu
-0.533
-0.336
-0.66±0.04
15.2±3.7
Sneden 96
238U/Os
-2.555
-1.27
-2.19±0.18
13.6±2.7
Cowan 99
238U/Ir
-2.616
-1.30
-2.10±0.17
11.8±2.5
Cowan 99
-0.255
-0.10
-0.74±0.15
-0.74±0.15
10.6±3.3
14.0±3.3
Cowan 99
Goriely 99
R
238U/ 232Th
Valor
medio
12.9±0.7
L’età misurata si riferisce al tempo di produzione del torio su una stella già
esistente dovuta all’esplosione di una supernova preesistente,
►l’età misurata è un limite inferiore per la stella e per l’universo.