x
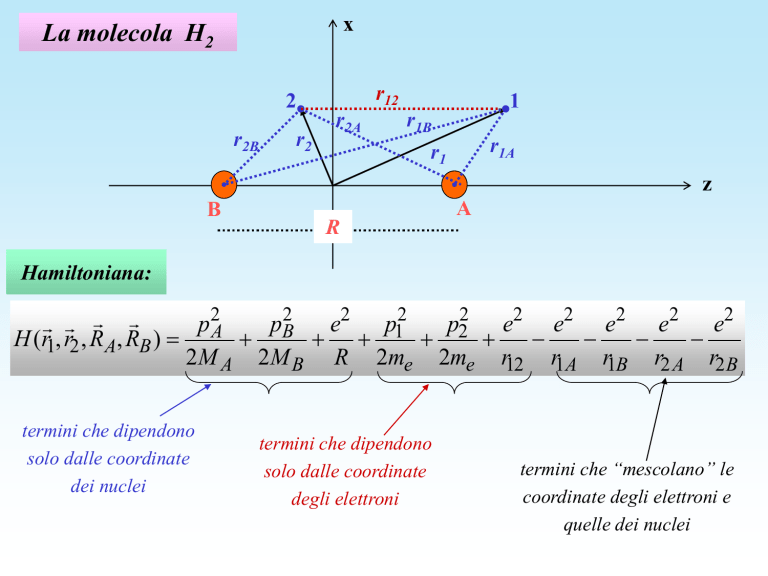
La molecola H2
2
r2B
r2
r12
r2A
1
r1B
r1
r1A
z
B
R
A
Hamiltoniana:
p2A
pB2
e2 p12
p22 e2 e2 e2 e2 e2
H ( r1, r2 , RA, RB )
2 M A 2 M B R 2me 2me r12 r1A r1B r2 A r2 B
termini che dipendono
solo dalle coordinate
dei nuclei
termini che dipendono
solo dalle coordinate
degli elettroni
termini che “mescolano” le
coordinate degli elettroni e
quelle dei nuclei
Equazione di Schrödinger:
La molecola H2
H ( r1, r2 , R A , RB ) ( r1, r2 , R A , RB ) E ( r1, r2 , R A , RB )
Approssimazione di Born-Oppenheimer:
data la grossa differenza fra la massa dell’elettrone e quella dei nuclei, è lecito
trascurare la variazione delle posizioni dei nuclei nella soluzione del moto degli
elettroni e risolvere l’equazione con una funzione d’onda prodotto della
funzione d’onda nucleare per una funzione d’onda elettronica con i nuclei
fermi a una distanza R.
funzione d’onda
R interviene come
funzione d’onda
elettronica con i nuclei
parametro e non come
nucleare
a distanza fissa R
variabile.
( r1, r2 , R A , RB ) R ( r1, r2 ) ( R A , RB )
energia degli elettroni con
i nuclei fissi a una
distanza R (non
necessariamente uguale a
quella di equilibrio)
R
H ( r1, r2 , RA , RB ) H el ( r1, r2 ) H nucl ( RA , RB )
R
R
H el ( r1, r2 ) R ( r1, r2 ) Eel R ( r1, r2 )
Equazione di Schrödinger per il moto dei nuclei
R
Sostituendo a H el ( r1, r2 ) il suo autovalore
EelR si ottiene:
2
2
p2
p
e
A
B
H nucl ( R A , RB ) ( R A , RB )
E el ( R ) ( R A , RB )
2M A 2M B
R
dove Eel (R) è ora una funzione
di R e non più una serie di
autovalori parametrizzati con R
repulsione fra i nuclei
e gli elettroni interni
e2
e2 b
E p ( R) E el ( R) 9
R
R R
attrazione fra gli ioni
esempio di Eel (R): legame ionico
esempio di potenziale interatomico: il potenziale di Morse
5
livello di energia
per atomi separati
4
potenziale (eV)
energia di
dissociazione D
3
parametri:
2
Ro 1/a
D=3,7 eV
1
Ro=2,5 Å
0
a = 0,6 Å-1
-1
0
Ro
5
10
15
R (angstrom)
e2
a ( R Ro ) 2
E p ( R)
E el ( R) D 1 e
R
confronto fra il potenziale di Morse e il potenziale ionico per Na Cl
5,0
potenziale ionico
potenziale
di Morse
potenziale (eV)
2,5
livello di energia
per ioni separati
0,0
parametri:
livello di energia
per atomi separati
D=3,7 eV
“energia di-2,5
Ro 1/a
dissociazione” D
Ro=2,5 Å
a = 0,6 Å-1
-5,0
0
E p( R) D 1 e
Ro
5
a ( R Ro ) 2
D
R (angstrom)
10
e2
b
E p ( R) 9
R R
15
e2 Ro8
; b
9
Separazione del moto del centro di massa e del moto relativo
R R A RB
M cm Rcm M A R A M B RB
x
RB
dove Mcm =MA +MB e Rcm sono la
massa e la coordinata del baricentro.
Si separa il moto traslatorio del baricentro e si studia
solo il moto relativo introducendo la massa ridotta :
RA
z
R
M AM B
M A MB
z
p2
H nucl ( R ) ( R )
E p ( R ) ( R )
2
R
potenziale a simmetria
sferica: coordinate sferiche R,
,
y
x
z
energia di vibrazione
moti
rotazionali
energia di rotazione
R
y
2
L2
pR
H nucl ( R, , ) ( R, , )
E
(
R
)
( R, , )
p
2
2 2 R o
x
distanza di equilibrio:
parametro non variabile
Erot
2
2 Ro2
l (l 1)
Erot
2
l (l 1) B rot l (l 1)
2
spettri rotazionali
2 Ro
1213
1112
01
12
89
23
45 56 67
34
regola di selezione: l =
910
1011
78
spettri “equispaziati”:
dalla spaziatura si risale al
valore di Brot e quindi di Ro
1
emissione
l = - 1 Erot = Brot [l (l+1)-(l-1)l]=2lBrot
assorbimento
l = + 1 Erot = Brot [l (l+1)-(l+1)(l+2)]=-2Brot (l+1)
l’andamento del potenziale
intorno al minimo è sempre
parabolico
Oscillazioni intorno alla
distanza di equilibrio
5
energia di
dissociazione D
potenziale (eV)
4
livello di energia
per atomi separati
potenziale “armonico”
Ep=1/2 2
3
= costante elastica
2
Ro 1/a
= spostamento da Ro
D=3,7 eV
1
Ro=2,5 Å
0
esempio: potenziale di Morse
a = 0,6 Å-1
-1
0
Ro
5
10
15
E p( R) D 1 e
R (angstrom)
Da 2 ( R Ro )2
2Da 2 2 3,7 (0,6 1010 m-1 ) 2 2,6 1020 eVm -2 40 Jm -2
valori di costanti elastiche macroscopiche!
a ( R Ro ) 2
2Da 2
oscillazioni intorno alla distanza di equilibrio
e2
10 Ro8
3 11 3 2 8
2
dR
R
R
R
R
d 2E p
2e 2
90b
tenendo conto che
e 2 Ro8
b
9
nel punto di equilibrio Ro:
20
Ro
8 10 eVm
-2
8 2 107 eVm
8 c
3
137 Ro 137 (2,5 1010 m) 3
2
1,3 10 Jm
-2
risulta maggiore con il calcolo da
potenziale ionico rispetto a Morse perché
la buca è più stretta intorno al minimo!
5,0
2,5
potenziale (eV)
d 2E p
dR 2
potenziale ionico
0,0
-2,5
potenziale
-5,0
di Morse 0
Chi ha ragione? Guardiamo l’energia di vibrazione
5
R (angstrom)
10
15
oscillazioni intorno alla
distanza di equilibrio
energia di
dissociazione
oscillatore armonico classico:
energia di
livello zero
1
Eo
2
(c)2
c2
per Na Cl 0,05 eV
massa ridotta:
932 MeV
932 MeV
13 109 eV
1
1
1
1
ANa ACl
23 35
massa ridotta
oscillatore armonico quantistico:
1
E v v
2
potenziale ionico, 2,6·1020 eV · m-2:
4 1014 8 1020 (eV )3
9
13 10 eV
0,05 eV
potenziale di Morse, 2,6·1020 eV · m-2:
4 1014 2,6 1020 (eV )3
9
13 10 eV
0,03 eV
oscillazioni intorno alla distanza di
equilibrio: correzione a grandi energie
potenziale di Morse:
E ( R) D 1 e
Da (R Ro )
a ( R Ro ) 2
2
2
1
( ) 1
E v v
v
4D 2
2
termine armonico
5,0
3
3
Da ( R Ro )
2
termine anarmonico
0,4eV
4,0
potenziale (eV)
2
13 14
12
11
10 9
8
3,0
2,0
7
6
5
4
a causa del termine
anarmonico i livelli
energetici si
addensano al crescere
dell’energia
3
1,0
2
1
0
0,0
0
2
4
6
R (angstrom)
8
10
1
energia di
Eo
livello zero, v=0
2
Energie rotovibrazionali
livelli e transizioni rotovibrazionali
spettri rotovibrazionali
932 MeV 932 MeV
0,9737 932 MeV
1
1,0270
1
37
932 MeV 932 MeV
H 35Cl c 2
0,9722 932 MeV
1
1,0286
1
35
H 37Cl c 2
=1/0,27·104 cm-1
=3,7 ·10-3 mm IR
vibrazioni in molecole poliatomiche
probabilità
eccitazione
probabilità relativa
di due di
livelli
di energie termica
E1 ed Eo:
P ( Eo E1 )
E1
Eo
Ce E1 / k BT
Ce Eo / k BT
E1
3
2
Eo
1
2
e ( E1 Eo ) / k BT
P( Eo E1 ) e / k BT
probabilità di eccitare il livello 2 vibrazionale di CO2
2f
2c
12.56 10 5 eV cm 667cm 1 0,08eV
P e / k BT e 0,08/ 0,03 0,07
eccitazione radiativa
E1
Eo
E1
3
2
Eo
1
2
fotone
fotone di energia E 0,08 eV 30 m lontano IR
La “linea di
inversione”
dell’ammoniaca