Costruzioni con riga e compasso e operazioni algebriche
Tra i testi che vengono diffusi in gran numero grazie all’invenzione della stampa, un posto rilevante
è occupato dalle edizioni dei classici della matematica greca, in particolare degli Elementi di
Euclide e delle Opere di Archimede e Apollonio. Gli Elementi sono il testo sul quale si formaranno
generazioni di matematici e più in generale di scienziati dal Rinascimento ai nostri giorni, un testo
pubblicato innumerevoli volte sia nell’originale greco sia soprattutto nelle traduzioni in latino prima
e poi nelle verie lingue nazionali. Dall’altra parte le Opere di Apollonio e Archimede, soprattutto
queste ultime, saranno fonte di ispirazione e occasione di ricerca per i matematici dl Cinquecento e
del Seicento. È a partire dai risultati del Siracusano che si prenderanno le mosse le indagini
moderne, che condurranno attraverso varie vicende all’invenzione del calcolo infinitesimale.
Il Cinquecento vede completarsi il processo di appropriazione e di assimilazione dei risultati di
Euclide e di Archimede. Se gli Elementi del primo erano già largamente noti anche nel Medioevo,
le opere del secondo diventeranno accessibili solo grazie alla loro pubblicazione a stampa. Lo
sviluppo delle ricerche pone subito il problema del metodo soggiacente alla scoperte dei geometri
antichi. Gli Elementi di Euclide, come pore le Opere di Archmede e Apollonio contengono
l’esposizione dei risultati nelle loro forma definitiva; in essi è evidente l’intento espositivo (la
concatenazione dei risultati, la stringatezza delle dimostrazioni, il gioco degli assiomi e dei
postulati), mentre è del tutto assente la descrizione del processo, spesso tortuoso e intuitivo, basato
più su ragionamenti plausibili che su inferenze rigorosamente logiche; che ha condotto alla
scoperta dei teoremi che vengono presentati e dimostrati. Questo silenzio pressoché totale genera la
convinzione dell’esistenza di un “metodo nascosto” di scoperta, diverso e distante da quello palese
dell’esposizione, che gli antichi avrebbero utilizzato nelle loro ricerche ma avrebbero poi occultato
nella comunicazione delle loro scoperte. Su questo metodo segreto si sono affaticati non pochi
matematici del Rinascimento.
Nel caso di Archimede, il sospetto doveva rivelarsi fondato all’inizio del secolo scorso, quando il
filologo danese Heiberg fece emergere da un palinsesto allora conservato a Costantinopoli un’opera
fin allora sconosciuta di Archimede, intitolata per l’appunto “Il Metodo”, in cui il Siracusano
rivelava –sotto forma di lettere a Conone e a * , due matematici alessandrini suoi corrispondenti– il
metodo di cui si serviva per trovare i risultati che poi avrebbe dimostrato rigorosamente nelle opere
pubblicate.
Per quanto riguarda gli Elementi di Euclide, la domanda riguardava soprattutto le costruzioni con
riga e compasso, spesso semplici ma talvolta molto complesse. La correttezza delle dimostrazioni
era evidente, ma quale strada aveva seguito Euclide per giungere alle costruzioni richieste? Non
essendoci pervenuto nessun “Metodo” euclideo, la questione è di difficile soluzione. I matematici
del Cinquecento e del Seicento tendevano per lo più a identificare il procedimento euclideo di
scoperta con il metodo di “analisi e sintesi” descritto da Pappo (un matematico alessandrino del V
secolo d. C.) e variamente interpretato.
Le parole di Pappo sono grosso modo le seguenti: l’analisi consiste nel considerare il problema
come risolto e partendo dalla soluzione nel dedurne via via una serie di affermazioni, finché si
giunge a una proposizione nota o perché dimostrata in precedenza o perché assunta come ipotesi. A
questo punto, mediante la sintesi, si procede a ritroso da questa proposizione fino a ritrovare il
risultato voluto.
Non sembra che il metodo così descritto da Pappo sia molto utile nelle costruzioni con riga e
compasso. A questo punto però si innesta nei procedimenti geometrici un nuovo filone, in gran
parte sconosciuto ai matematici classici: l’algebra. Grazie alla nuova disciplina, l’analisi e sintesi
vengono rilette in termini algebrici: si considera il problema come risolto e trattando allo stesso
modo i segmenti noti e quelli incogniti (l’unica differenza, seguendo Descartes, sarà che per
distinguere gli uni dagli altri si designeranno le incognite con le ultime lettere dell’alfabeto e le
quantità note con le prime) si tradurranno le relazioni geometriche tra i segmenti in questione in
equazioni algebriche. Eliminate le variabili tra le diverse equazioni, si giungerà –se il problema è
determinato– a un’equazione in una sola incognita, la cui soluzione verrà poi riletta in termini
geometrici e indicherà la strada da seguire per la costruzione del problema. Abbiamo così di nuovo
una separazione del procedimento in analisi e sintesi, o anche risoluzione e composizione. L’analisi
(o la risoluzione) consiste nel porre il problema in equazioni algebriche e nella soluzione di queste
ultime; la sintesi (o composizione) nell’interpretazione della formula o dell’algoritmo risolutivo in
termini di operazioni geometriche con riga e compasso e di conseguenza nella costruzione
geometrica della soluzione.
Finché l’algebra era soprattutto “numerica”, ossia finché i coefficienti delle equazioni in gioco
erano dati in forma numerica, non esisteva una “formula risolutiva” delle equazioni di secondo
grado, ma la loro soluzione erqa data sotto forma di un algoritmo, una ricetta buona per tutti i casi.
Ad esempio, la soluzione del “capitolo di censo (x2) e cose (ax) uguali a numero (b)”, ovvero nella
terminologia di Bombelli, di “potenza e tanti eguali a numero” (cioè dell’equazione x2+ax=b)
veniva espressa così:
Quando si haveranno Potenza e Tanti eguali a Numero … si piglia la metà delli Tanti, e si
quadra, ed il prodotto si aggiunge al Numero, e della somma se ne pigli il lato, e dal detto lato
se ne cava la metà delli Tanti, e quello che restarà sarà la valuta del Tanto.
che si può tradurre in termini moderni così:
Quando si haveranno Potenza e Tanti eguali a Numero [x2+ax=b]
si piglia la metà delli Tanti [a/2] e si quadra [(a/2)2]
ed il prodotto si aggiunge al Numero [(a/2)2+b]
e della somma se ne pigli il lato
(a / 2) 2 + b
e dal detto lato se ne cava la metà delli Tanti
(a / 2) 2 + b − a / 2
e quello che restarà sarà la valuta del Tanto
x = (a / 2) 2 + b − a / 2
Più avanti, con la pubblicazione delle opere di Viète, viene introdotta l’algebra speciosa, cioè
l’algebra letterale moderna, in cui sia le incognite che i dati del problema sono indicati con delle
lettere. Lo stesso Viète mostra come eseguire con riga e compasso le operazioni algebriche
elementari e con qureste risolvere le equazioni di secondo grado o biquadratiche. Un suo allievo,
Marino Ghetaldi, scriverà un importante volume in cui il metodo algebrico viene usato
sistematicamente per le costruzioni con riga e compasso.
Viète usa le vocali per denotare le incognite e le consonanti per le quantità note; meno di
cinquant’anni dopo, Descartes introdurrà le notazioni algebriche in uso tuttora, in cui le ultime
lettere dell’alfabeto, x, y, z sono usate per indicare quantità incognite e le prime lettere indicano
quantità note. Con Descartes le notazioni algebriche assumono la forma attuale.
Contemporaneamente, perde di importanza la parte “sintetica” della costruzione geometrica, a tutto
vantaggio della parte analitica. Non a caso la geometria introdotta da Descartes si chiama
“geometria analitica”. In essa, una curva piana è rappresentata direttamente da un’equazione in due
variabili (le coordinate cartesiane) e i problemi e le relative le operazioni geometriche vengono
tradotti immediatamente in analoghi problemi e relazioni algebriche. Vengono così
progressivamente svalutate le ricerche relative alle costruzioni geometriche, sia quelle con riga e
compasso che quelle in cui intervengono curve di ordine superiore, anche se il problema della
“costruzione delle equazioni” (cioè del tracciamento delle curve rappresentate da equazioni
algebriche e in alcuni casi trascendenti) resta pur con un ruolo secondario fino alla fine
dell’Ottocento (teorema di Kempe).
Vediamo ora come sia possibile utilizzare l’algebra per la soluzione di problemi geometrici
mediante costruzioni con riga e compasso. Per semplificare la trattazione, utilizzeremo le notazioni
cartesiane anche quando i problemi esaminati sono presi da autori precedenti, in particolare
dall’Algebra di Raffaele Bombelli.
Con riga e compasso si possono eseguire sui segmenti le quattro operazioni aritmetiche ed estrarre
la radice quadrata.
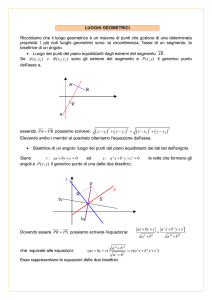
1. Somma e differenza.
Dati due segmenti a=AB e b=CD, costruire i segmenti somma a+b e differenza a-b. Quest’ultima
operazione è possibile solo se a>b.
B
a
A
C
b
D
Si trasporta il segmento CD con un estremo in B (Elem. I.2)
a
A
C
B
b
D
Si prolunga ora il segmento AB (Elem. I, Post. 2) e si traccia la circonferenza di centro B e raggio
BD (Elem. I, Post. 3), che incontra il segmento AB in F e il suo prolungamento in E.
Il segmento AE è la somma a+b di AB e CD, mentre AF è la differenza a–b.
2. Prodotto e quoziente.
Dati tre segmenti, di lunghezza a, b e c, si tracci un angolo arbitrario POQ. A partire dal vertice O si
riporti OA=a, OB=b e BC=c.
Si congiunga il
CD parallela ad
teorema di
segmento AB e si tracci
AB. Sia d = AD. Per il
Talete si ha
a:b=d:c
e dunque
ac
d= .
b
La costruzione vale sia per il prodotto che per il quoziente; infatti se si prende b=1 si ha d=ac,
mentre se c=1 risulta d=a/b.
3. Sottomultipli di un segmento.
Il teorema di Talete permette anche di dividere un segmento in un qualsiasi numero di parti uguali.
Costruire un multiplo di un segmento è moilto facile: basta sommare tanti segmenti uguali. Magari
per sveltire le operazioni, ad esempio se si vuole moltiplicare un segmento AB per 7, si può
raddoppiare, poi raddoppiare di nuovo e poi ancora una volta, in modo da moltiplicarlo per 8. Il
segmento B8 è sette volte AB..
Per dividere un segmento AB in un certo numero di parti uguali, ad esempio 5, si prende un
segmento arbitrario CD e lo si moltiplica per 5.
Si
hanno così sulla stessa
retta
cinque segmenti uguali
A1, 12,
23, 34 e 45. Si riporta
ora con un angolo qualsiasi il segmento AB che si vuole dividere in cinque parti uguali. Si traccia la
retta B5, e poi dai punti 1, 2, 3 e 4 si tracciano le parallele a B5, che incontreranno il segmento AB
nei punti C, D, E ed F- Per il teorema di Talete, i cinque segmenti AC, CD, DE, EF e FB sono
uguali, e quindi il segmento AB risulta diviso in cinque parti uguali.
4. La radice quadrata.
Occorre considerare tre tipi di radici:
a2 + b2 , a2 − b2 e
ab .
Vediamole in ordine.
4.1.
a2 + b2 .
Consideriamo due segmenti, di lunghezza a e b. Per costruire il segmento di lunghezza
basta disporre i due segmenti perpendicolarmente uno su un estremo dell’altro.
a2 + b2 .
Completato il triangolo rettangolo, per il teorema di Pitagora (Elem. I.32*) l’ipotenusa c avrà
lunghezza
a2 + b2 .
4.2.
a2 − b2 .
Sempre usando il teorema di Pitagora si può costruire il segmento di lunghezza
a2 − b2 .
Siano a e b le lunghezze di due segmenti, con a>b. Sopra il segmento AB di lunghezza a si tracci la
semicirconferenza AFB. Con centro A e raggio b si tracci una circonferenza (non presente nel
disegno), che incontra la semicirconferenza AFB in F. Questa intersezione esiste sempre perché si è
supposto a>b. Il triangolo AFB è rettangolo e quindi per teorema di Pitagora, il segmento FB ha
lunghezza
c = a2 − b2
4.3.
ab .
Si può procedere in due modi. Il primo consiste nel riportare i due segmenti a=AB e b=BD sulla
stessa retta (come abbiamo fatto per la somma).
Trovato ora il punto di mezzo E del segmento AD (Elem. I.10), si tracci la semicirconferenza di
centro E e raggio EA=ED. Dal punto B si tiri la perpendicolare al segmento AD (Elem. I.11), che
incontra la semicirconferenza in F. Il triangolo AFD è rettangolo, e quindi per il secondo teorrema
di Euclide il quadrato su FB è equivalente al rettangolo sui segmenti AB e BD. Se si pone FB=c, si
ha dunque c2=ab, e quindi
c = ab .
Un secondo modo sfrutta il primo teorema di Euclide. Si supponga a>b (se a<b basta scambiare i
due segmenti; se a=b la radice cercata è a) e sul diametro AB=a si tracci la semicirconferenza ABF.
Sul diametro si riporti il segmento BD=b e dal punto D si tiri la perpendicolare CF che incontra la
semicirconferenza in F.
Per il primo teorema di Euclide, il quadrato del cateto BF è equivalente al rettangolo che ha per lati
l’ipotenusa AB e la proiezione DB del cateto sull’ipotenusa. Detta d la lunghezza di CF, si ha allora
d2=ab, e quindi
d = ab .
Notiamo che se si vuole costruire la radice di a, basterà prendere uguale a 1 la lunghezza b del
segmento DB.
5. Le equazioni di primo grado.
La costruzione geometrica corrispondente a un’equazione di primo grado è molto semplice. Infatti
l’equazione
bx=ac
ha come soluzione x=ac/b, che può essere costruita come abbiamo visto in 2. In particolare,
l’equazione bx=a si costruisce come detto, prendendo c=1.
6. Le equazioni di secondo grado.
Nell’algebra dei segmenti che abbiamo studiato finora, le grandezze a, b, c, così come l’incognita x,
denotano sempre lunghezze di segmenti, e quindi sono sempre positive. Di conseguenza, non
abbiamo un solo tipo di equazioni di secondo grado, ma tre, e precisamente
[1] x2+ax=b2
[2] x2=b2+ax
[3] x2+b2=ax
Non si prende in considerazione un quarto tipo di equazione, e precisamente x2+ax+b2=0, perché le
sue eventuali radici sono necessariamente negative.
Notiamo che abbiamo scritto il termine noto nella forma b2 per far sì che i diversi termini siano
omogenei, cioè tutti di dimensione 2. Se si scrive l’equazione nella forma usuale, ad esempio
x2+ax=c, occorrerà per prima cosa costruire un segmento b con b2=c.
La soluzione geometrica di queste equazioni consiste, dati due segmenti di lunghezza a e b, nel
costruire con riga e compasso il segmento di lunghezza x, soluzione dell’equazione data.
Vediamo i tre casi in ordine. La soluzione della prima equazione è
2
a
a
x = − ± + b2
2
2
ma poiché la lunghezza x deve essere positiva, si dovrà scegliere il segno +. Avremo dunque
2
a
a
x = − + + b2
2
2
Per la seconda, sempre prendendo la sola soluzione positiva, si ha
2
a
a
x = + + b2
2
2
Per la costruzione geometrica occorre prima dividere a metà il segmento a, poi costruire la radice
secondo il procedimento visto sopra, dalla quale occorre infine sottrarre (nel primo caso) o
sommare (nel secondo) il segmento a/2. La figura spiega i vari passi:
1. Si divide a metà il segmento a.
2. Su un estremo A del segmento AB=a/2 si tira la perpendicolare AC di lunghezza b.
3. Si costruisce il triangolo rettangolo ABC di cateti AB= a/2 e AC=b. La sua ipotenusa BC vale
2
a
2
+b
2
4. Con centro nel vertice B del triangolo ABC e raggio a/2 si traccia una circonferenza, che incontra
l’ipotenusa in D e il suo prolungamento in E. Poiché DB=BE= a/2, si avrà
2
a
a
CD = + b 2 −
2
2
e
2
a
a
CE = + b 2 +
2
2
Di conseguenza il segmento CD è la soluzione x dell’equazione [1], mentre CE è la soluzione
dell’equazione [2].
In questo modo si possono costruire con riga e compasso dei problemi geometrici, come il seguente
preso dall’Algebra di Raffaele Bombelli:
Trovami un rettangolo che sia pari al quadrato LIK, e che li due suoi lati sia uno maggiore
dell’altro la linea D.
Per porre questo problema in equazione, chiamiamo b il lato del quadrato LIK e a la lunghezza
della linea D. Se x è il più piccolo dei lati del rettangolo, l’altro sarà a+x, e dunque l’area del
rettangolo x(a+x) dovrà essere uguale a quella del quadrato b2. Avremo allora x(a+x)=b2, ossia
x2+ax=b2. Il lato minore è dunque il segmento CD nella costruzione precedente. Per trovare il lato
maggiore basta sommare a questo il segmento DE di lunghezza a, trovando così il segmento CE. In
conclusione, i lati del rettangolo sono CD e CE.
Resta da indagare la costruzione dell’equazione [3], che ha due soluzioni positive
2
a
a
x = ± − b2
2
2
purché risulti a/2>b. Se invece a/2<b, non ci sono soluzioni reali, mentre se a/2=b c’è una sola
soluzione x=a/2, la cui costruzione è immediata. Consideriamo allora il caso a/2>b.
La costruzione della radice l’abbiamo vista sopra. Sul segmento AB=a/2 si costruisce una
semicirconferenza ACB; poi con centro A e raggio b si traccia una seconda circonferenza (non
presente nel disegno) che incontra la prima in C. Il triangolo ACB è rettangolo, e quindi il segmento
c=CB ha lunghezza
2
a
2
−b
2
Per trovare le due soluzioni bisogna aggiungere o togliere questa radice dal segmento AB=a/2.
Descritta allora la circonferenza di centro B e raggio BC, le due soluzioni saranno rispettivamente i
segmenti AD ed AE.
Un problema geometrico corrispondente si trova ancora nell’Algebra di Bombelli:
Voglio dividere la linea AZ in due tal parti delle quali fattone un rettangolo sia pari al quadrato
LIK.
Detta a la lunghezza della linea AZ, e x una delle parti, l’altra sarà a–x. Si avrà allora l’equazione
x(a–x)=b2, dove b è il lato del quadrato LIK. L’equazione corrispondente è dunque x2+b2=ax, che
abbiamo appena studiato, e le due parti della linea sono i segmenti AE ed AD costruiti sopra.
7. Le equazioni biquadratiche.
Le costruzioni delle equazioni di secondo grado possono servire per le equazioni biquadratiche.
Cominciamo con un esempio, tratto anche questo dall’Algebra di Bombelli.
Trovami due linee che, fatto su di esse un rettangolo, sia pari al quadrato LIK e che fatto di
ciascuna di esse un quadrato, il maggiore meno il minore sia pari al rettangolo IKM [con un lato
uguale al lato del quadrato].
Siano x il minore e y il maggiore dei due segmenti cercati, sia a il lato del quadrato LIK e siano a e
b i lati del rettangolo IKM..
I
a
L
a
a
K
b
Dovremo avere
xy=a2
y2–x2=ab
Dalla prima equazione ricaviamo y=a2/x, e dalla seconda
a4
− x 2 = ab
2
x
M
e quindi
a4=x4+abx2.
La soluzione di questa equazione è
x2 = −
2
2
b
ab
b
ab
+ + a 4 = a − + + a 2
2
2
2
2
Cominciamo a costruire la quantità tra parentesi, che chiasmiamo z. La radice esprime la diagonale
del rettangolo di lati a e b/2, dunque è uguale al segmento IH. Per ottenere la quantità z tra parentesi
occorre sottrarre b/2.
Questo si può fare riportando il segmento IH sulla base LH, cioè descrivendo una circonferenza
con centro in H e raggio HI. Il segmento EH è allora uguale a IH, e sottraendo KH=b/2 si ottiene
z=EK.
A questo punto si deve costruire il segmento x = az . Ricordando che LK=a, si riporta KF=z e
sul segmento LF si costruisce la semicirconferenza LGF, che incontra il lato IK in G. Il segmento
KG è la soluzione x; infatti per il secondo teorema di Euclide si ha LK×KF=GK2, e quindi il
segmento GK è la radice di az.
Osserviamo che perché questa costruzione funzioni, è necessario che l’equazione sia della forma
x4+abx2=a4. Questa naturalmente non è la forma più generale di un’equazione biquadratica di
questo tipo; se si ha a che fare con un’equazione biquadratica generale:
x4+hkx2=pqrs
Occorre prima di procedere ridurla alla forma precedente. Per questo si comincia dal secondo
membro, costruendo per mezzo del teorema di Euclide (§ 4.3) le radici c = pq e d = rs .
Avremo allora pqrs = c2d2. Sempre utilizzando il teorema di Euclide, si costruisce a = cd
e quindi pqrs = c2d2=a4.
A questo punto possiamo porre b=hk/a (§ 2) da cui hk = ab. In questo modo l’equazione diventa
x4+abx2=a4, la cui soluzione può essere costruita con riga e compasso come visto sopra.
8. Problemi più complessi.
Negli esempi visti finora, i coefficienti dell’equazione risolvente erano combinazioni molto
semplici dei dati del problema. Quando ciò non avviene, le cose si complicano e le costruzioni
diventano più complesse. Vediamo un esempio, sempre tratto dall’Algebra di Bombelli.
Facciasi della linea BE due parti, che fatti di esse parti due quadrati, et aggiunti insieme, siano
pari al quadrato fatto dalla linea [data] A col agiungerli un rettangolo fatto dalle due parti di detta
linea.
Sia a la lunghezza del segmento BE, b quella del segmento A e sia x la più piccola delle due parti in
cui è diviso il segmento BE. L’altra parte sarà allora a–x, e dovremo avere
x2+(a–x)2=b2+x(a–x).
Siccome la somma dei due quadrati a primo membro è minore di a2, mentre il secondo membro è
maggiore di b2, perché il problema sia risolubile deve essere a>b. Sviluppando e raggruppando i
termini nell’equazione precedente si giunge all’equazione
x2 +
a2 − b2
= ax
3
che ha come soluzioni
a
a2 − b2
a
.
± −
2
3
2
2
Poiché avevamo supposto che x fosse la parte più piccola del segmento BE, occorrerà prendere il
segno –. Avremo allora
a
a2 − b2
a
x= − −
.
2
3
2
2
Come al solito, la costruzione con riga e compasso comincia dalla radice. Dato che a>b, i due
termini sotto radice sono positivi, e quindi la costruzione sarà quella per
p2 − q2
Nel nostro caso, p è a/2, mentre q2=(a2–b2)/3. Bisognerà dunque costruire in primo luogo la quantità
a2 − b2
.
3
Ora noi sappiamo costruire
sappiamo invece come
radice.
a2 − b2
(§ 4.2) e dunque
fare quando il 3 è
a2 − b2
3
Per questo ci viene in aiuto la costruzione della radice del § 4.3. Infatti si ha
a2 − b2
.=
3
a2 + b2 ×
a2 + b2
3
anche (§ 3). Non
all’interno della
e poiiché, come abbiamo visto, sappiamo costruire i due fattori sotto la radice a destra, sapremo
costruire anche la radice a primo membro.
A questo punto possiamo procedere con la costruzione, cominciando da
Sul segmento BE=a tracciamo un semicerchio, sul quale con centro in B
individuiamo il punto A. Completiamo il triangolo rettangolo BAE, che
AE =
a2 − b2
.
3
a2 − b2
e raggio b
avrà il lato
Ciò fatto dividiamo il segmento AE in tre parti uguali, di cui una sia CE. Si avrà dunque
CE =
a2 − b2
3
Costruiamo poi un semicerchio sul diametro AE, e dal punto C tiriamo la perpendicolare ad AE,
che incontrerà il semicerchio nel punto D. Congiungiamo DA e DE. Il triangolo ADE è rettangolo,
e per il teorema di Euclide il quadrato sul cateto DE è equivalente al rettangolo che ha come lati
l’ipotenusa AE e la proiezione di DE sull’ipotenusa. Si ha dunque DE2=AE×CE, e dunque
DE 2 = a 2 − b 2 ×
Il
A
a2 − b2 a2 − b2
=
.
3
3
segmento q=DE è dunque quello cercato.
questo punto possiamo costruire la
soluzione del problema.
Sul segmento DF=a/2 si costruisce un semicerchio. Con centro in D e raggio il segmento q=DE
trovato in precedenza si determina il punto E sul semicerchio. Si completa il triangolo rettangolo
DEF, il cui cateto EF sarà uguale a
a2 − b2
a
a
2
.
−q = −
3
2
2
2
2
Per concludere, bisognerà sottrarre questa quantità da a/2. Questo si fa tracciando un arco di
cerchio con centro F e raggio EF. Risulta GF=EF, e dunque DG è il segmento cercato.