A.A. 03-04 Elettronica - Soluzioni della prova scritta del 05/07/04 1
annuncio pubblicitario
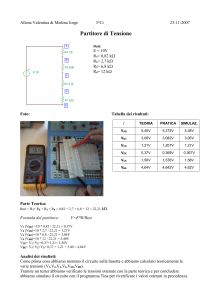
A.A. 03-04 Elettronica - Soluzioni della prova scritta del 05/07/04 1) Dallo schema segue immediatamente che: VGS = VDD per cui, siccome VGS − VTH ≈ 2.55 V, risulta soddisfatta la disuguaglianza: VDS < VGS − VTH . Pertanto il transistor opera in regione di triodo e la corrente di drain è data dalla relazione: W I D = kn L 2 2 (VGS − VTH ) VDS − VDS , dove: ID = VDD − VDS ≈ 30 µA. R Sostituendo, quindi, nella relazione precedente, si ha: ID W = ≈ 0.67. 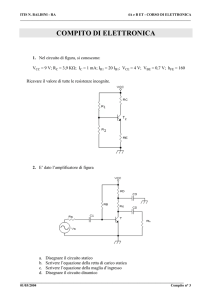L kn 2 (VGS − VTH ) VDS − VDS 2 2) Considerando i condensatori dei circuiti aperti si ottiene lo schema di figura. Assumendo che il BJT sia in zona lineare, con VBE pari a 0.7 V, applicando la KVL al circuito di ingresso si trova: +VCC IB VEE − VBE = R1 I B + ( R4 + R5 ) I E = R1 IE + I ( R + R5 ) , β +1 E 4 da cui segue: IE = VEE − VBE ≈ 2.0 mA; R1 + R + R5 β +1 4 quindi, applicando la KVL al circuito di uscita si ha: R1 R2 IE VCE IE VBE R4 R5 -VDD VCE = VCC + VEE − RC I C − ( R4 + R5 ) I E = = VCC + VEE − RC I E β β +1 − ( R4 + R5 ) I E ≈ 6.2 V . Siccome VCE > 0.7 V , il BJT opera effettivamente in zona lineare. Nel punto di funzionamento, la corrente di collettore vale: IC = IE ≈ 2.0 mA, β +1 così i parametri del modello a π sono: I mA g m = C ≈ 76.6 , V VT rπ = β gm vbe C1 vin + rp R1 R4 R2 R5 ≈ 1.3 kΩ. 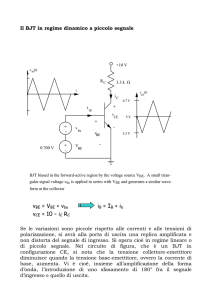C3 gm vbe R3 v out C2 In figura è mostrato il circuito equivalente per il piccolo segnale; considerando i condensatori dei cortocircuiti, lo schema si modifica come indicato in figura vbe seguente, in cui la resistenza RC vale: N RC = R2 R3 ≈ 2.1 kΩ R2 + R3 vin + R1 rp R4 gm vbe RC ie Applicando la KVL al circuito di ingresso risulta: vi = vbe + R4ie dove la corrente ie può esprimersi attraverso vbe applicando la KCL al nodo N: ie = g m vbe + vbe rπ inoltre la tensione vout può scriversi come: vout = − g m vbe RC , per cui: vbe = − vout . g m RC Quindi, sostituendo nelle precedenti espressioni, si trova: v out vi = − vout g m RC 1 R4 R R + 4 + 4 1 + g m R4 + = −vout rπ g m RC RC β RC , da cui segue: Av = − g m RC R 1 + g m R4 + 4 rπ =− β RC rπ + R4 (1 + β ) ≈ -6.7, vbe C1 g v m be che corrisponde a circa 17 dB. Per calcolare la costante rp di tempo associata al condensatore C1 , dopo aver R4 RC R1 annullato il generatore d’ingresso, sostituiamo tutti gli altri condensatori con dei cortocircuiti. Lo schema si Re1 R'e1 modifica così come mostrato in figura. La resistenza Re1 vista dal condensatore C1 è pari al parallelo di R1 con la resistenza Re′1 posta a valle di R1 . Per valutare tale quantità stabiliamo la resistenza equivalente del circuito a destra di R1 . Applichiamo, pertanto, un generatore di tensione e stabiliamo la corrente erogata. Risulta: v1 = i1rπ + ( i1 + i1 g m vbe ) R4 = i1 rπ + R4 (1 + β ) , vbe i1 da cui segue: v1 + rp gm vbe R4 RC i 1 + gm vbe Re′1 = v1 = rπ + R4 (1 + β ) ≈ 31.6 kΩ. i1 Così la resistenza Re1 vale: Re1 = R1 Re′1 ≈ 1.9 kΩ, R1 + Re′1 e quindi la costante di tempo τ 1 associata a C1 è: vbe rp gm vbe N R4 R5 τ 1 = Re1C1 ≈ 376 ms. 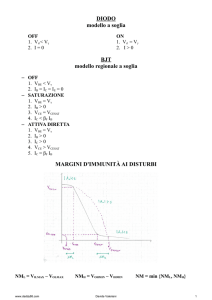RC C2 Per calcolare la costante di tempo associata a C2 procediamo in maniera analoga; in figura è mostrato il corrispondente circuito. Allo scopo di semplificare la vbe determinazione escludiamo il ramo compreso tra il nodo N e gm vbe massa e stabiliamo la resistenza equivalente Re′2 vista da questi i2 rp + due morsetti. Applichiamo, pertanto, un generatore di tensione RC v2 e stabiliamo la corrente erogata; poiché risulta vbe = −v2 , segue: i2 = − g m vbe − vbe 1 = −vbe g m + rπ rπ 1 = v2 g m + rπ , e quindi: Re′2 = r v2 1 = = π ≈ 12.9 Ω. i2 g + 1 1 + β m rπ N R'e2 Così, con riferimento alla figura, la resistenza Re 2 vale: Re 2 ( R′ + R4 ) R5 = e2 Re′2 + R4 + R5 R4 R5 C2 ≈ 295.5 Ω, e quindi la costante di tempo τ 2 associata a C2 è: τ 2 = Re 2C2 ≈ 8 ms. Infine calcoliamo la costante di tempo associata a C3 ; per semplificare il calcolo escludiamo il ramo posto a sinistra di R2 e valutiamone la resistenza equivalente Re′3 . Pertanto applichiamo un generatore di tensione e stabiliamo la corrente erogata; siccome risulta: i= 1 vbe + g m vbe = vbe + g m , rπ rπ allora, poiché vbe + iR4 = 0 , segue: vbe rp C3 gm vbe R4 R3 R2 R'e3 vbe rp gm vbe R4 i v3 + i3 1 vbe + vbe R4 + g m = 0 rπ che è soddisfatta solo se vbe = 0 . Quindi anche i = 0 e pertanto la resistenza Re′3 è infinita. Così, dal circuito di figura segue che la resistenza Re3 vista C3 vale: Re3 = R2 + R3 ≈ 9.3 kΩ. Ne segue che la corrispondente costante di tempo è: τ 3 = Re3C3 ≈ 930 ms. La frequenza di taglio inferiore dell’amplificatore vale quindi: C3 R2 R3 fL = 1 2π 1 1 1 + + ≈ 20 Hz. τ1 τ 2 τ 3 Si noti che la frequenza di taglio è dominata dal polo associato alla capacità C2 che, da solo, determina una frequenza di taglio 1 ( 2πτ 2 ) pari a 19.9 Hz, mentre le frequenze di taglio associate alle capacità C1 e C3 sono, rispettivamente, 50 e 100 volte minori.
