Pubblicazioni

Il BJT in regime dinamico a piccolo segnale
+10 V
v be(t)
0.008 V
RC
3.3 k 
t
v (t)
iC
i
-0.008 V
CE
6.7 V
+
B
t
v
CE
5V
+
0.700 V
+
-
v
-
+
-
V
be
vBE
3.3 V
-
BE
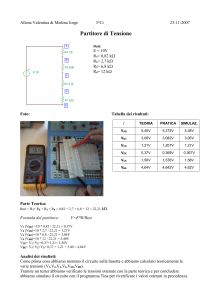
BJT biased in the forward-active region by the voltage source VBE. A small triangular signal voltage vbe is applied in series with VBE and generates a similar waveform at the collector
vBE = VBE + vbe
vCE = 10 – iC RC
iB = IB + ib
Se le variazioni sono piccole rispetto alle correnti e alle tensioni di
polarizzazione, si avrà alla porta di uscita una replica amplificata e
non distorta del segnale di ingresso. Si opera cioè in regime lineare o
di piccolo segnale. Nel circuito di figura, che è un BJT in
configurazione CE, si nota che la tensione collettore-emettitore
diminuisce quando la tensione base-emettitore, ovvero la corrente di
base, aumenta. Vi è cioè, insieme all’amplificazione della forma
d’onda, l’introduzione di uno sfasamento di 180° fra il segnale
d’ingresso e quello di uscita.
4.0mA
t
VBE= 0.717 V
I = 30 uA
B
C 3.0mA
o
l
l
e
c
t
o
r 2.0mA
Vce(t)
V = 0.708 V
BE
I = 20 uA
B
C
u
r
r
e
n
t 1.0mA
vbe(t)
Q-point
t
V = 0.700 V
BE
I = 15 uA
B
V = 0.692 V
BE
I = 10 uA
B
Load Line
0A
0V
2V
4V
6V
8V
10V
12V
Collecter-emitter Voltage
Load line, Q-point and signals for the CE circuit
Il funzionamento di un BJT in regime lineare può essere analizzato
con l’ausilio di un modello circuitale che utilizza parametri circuitali
in forma di impedenze, ammettenze e generatori controllati. La
tipologia di questi parametri dipenderà dalla scelta delle variabili
indipendenti che viene fatta alla porta d’ingresso e alla porta di
uscita. Individuando come variabili dipendenti le correnti i1 e i2 e
come variabili indipendenti le tensioni v1 e v2, la descrizione del
comportamento in regime lineare sarà effettuata per mezzo dei
parametri Y:
i1
i2
+
+
1
y
v
y v
11
1
12 2
1
y
y v
21 1
v
2
22
-
-
The y-parameter representation for a two-port network
i1 = y11v1 + y12 v2
i2 = y21v1 + y22 v2
costituisce la descrizione analitica dei legami fra tensioni e
correnti in questo modello
ic
+
ib
Q
+
v
be
v
ce
-
-
Two-port representation of the npn transistor
ib = y11vbe + y12 vce
ic = y21vbe + y22 vce
queste grandezze rappresentano le componenti variabili delle tensioni
e delle correnti totali, ovvero le piccole variazioni rispetto ai valori
corrispondenti al punto di polarizzazione.
I parametri y che individuano il comportamento del dispositivo in
regime di piccolo segnale saranno legati al punto di polarizzazione e
determinati come segue:
y11 = ib/vbe @ vce = 0
y12 = ib/vce @ vbe = 0
y21 = ic/vbe @ vce = 0
y22 = ic/vce @ vbe = 0
ciò equivale a calcolare la derivata parziale di ciascuna corrente
rispetto a ciascuna tensione intorno al punto di polarizzazione.
Quindi i parametri a piccolo segnale dipendono dal punto di
polarizzazione e vengono anche definiti parametri differenziali.
In un buon BJT possiamo ritenere trascurabile l’effetto del generatore
y12 vce cioè sostituirlo con un circuito aperto, semplificando il circuito
equivalente. Per quanto riguarda il parametro y11 si ha:
y11 = IC / o VT
dove o è definito guadagno per piccoli segnali a
emettitore comune ed è legato all’andamento
del guadagno di corrente in continua F in
funzione della corrente di collettore
F
o > 
 o< 
F
F
i
C
IM
DC current gain F versus current for the BJT
Il guadagno o quindi non è costante e tale che o>F per IC< IM mentre
o < F per IC > IM . E’ esattamente uguale a F per IC = IM dove la
derivata della funzione F ( IC ) si annulla.
Definendo i seguenti parametri:
Transconduttanza:
gm = y21 = IC/VT
Resistenza differenziale d’ingresso:
r = 1/y11 = o/gm
Resistenza differenziale di uscita:
r= 1/y22 = (VA + VCE )/ IC
si arriva alla rappresentazione mediante il modello cosiddetto a ibrido per piccoli segnali.
Ancora una volta si noti come i parametri sono dipendenti dalla scelta
del punto di polarizzazione. La transconduttanza è direttamente
proporzionale alla corrente di collettore, mentre le resistenze
differenziali d’ingresso e di uscita sono inversamente proporzionali
alla corrente di collettore. La resistenza differenziale mostra una
debole dipendenza dalla tensione collettore-emettitore (generalmente,
infatti, VA >>VCE).
Dalle espressioni relative ai parametri ibridi si evidenzia il legame
o = gm r
ic
ib
B
+
+
v
be
C
r
r
g v
m be
-
v
ce
E
Hybrid- small-signal model for the intrinsic bipolar transistor
Si definisce inoltre il fattore di amplificazione f dato da:
f = gm ro = (VA + VCE )/ VT
Esso rappresenta il massimo guadagno di tensione che un dato
transistore può fornire e non varia in funzione della polarizzazione.
ib
B
C
i
B
ic
b
C
+
v
r
be
g v

r
m be
r


 oib
r
(a)
(b)
E
E
Two equivalent forms of the BJT small-signal model
(a) Voltage-controlled current source model
(b) Current-controlled current source model
Modello lineare a parametri h
v1 = h11i1 + h12 v2
i2 = h21i1 + h22 v2
vbe = hieib + hre vce
CE
ic = hfeib + hoe vce
i1
+
v
1
i2
h
11
h v
12 2
h i
21 1
1
h
22
+
v
2
-
General two-port h-parameter representation
Da un punto di vista operativo si definisce il BJT in funzionamento a
piccoli segnali (condizione di linearità) quando:
vbe << 2VT
|vbe| ≤ 5 mV
che comporta ic / IC = 0.2 cioè una variazione della corrente di
collettore pari al 20%.
IC
iB
iC
ic
V CC
ib
IB
NPN
DC bias and signal currents for the npn transistor
Nell’analisi dei circuiti in regime dinamico lineare si sostituirà al BJT
il suo modello equivalente con valori appropriati degli elementi
(dipendenti dal punto di polarizzazione) e si ricaveranno le prestazioni
del circuito complessivo considerando anche l’effetto dei componenti
esterni. Tale analisi viene condotta considerando:
a) i generatori di tensione continua e i condensatori come
dei cortocircuiti
b) i generatori di corrente continua e gli induttori come dei
circuiti aperti
L’analisi del circuito in continua, d’altra parte, per la determinazione
del punto di polarizzazione viene fatta considerando:
a) i condensatori come circuiti aperti
b) gli induttori come corto circuiti
Questa separazione in due fasi è resa possibile dal principio di
sovrapposizione degli effetti, basato sulla condizione di linearità e
cioè di piccolo segnale.
V
R
CC
= 12 V
RC
2
4.3 k 
30 k 
RS
C1
•
C2
•
+
R
3
v
O
1k
v
100 k 
S
R
-
1
R
10 k 
E
•
C3
1.3 k 
Common-emitter amplifier circuit employing a bipolar transistor
R
S
Q
1k 
v
s
R
R
R
R
C
30 k 
+
vo
2
1
10 k 
3
4.3 k 
Thevenin Transformation
AC equivalent circuit for the common-emitter amplifier.
The common-emitter connection should now be evident.
100 k 
-
R
th
+
Q
R
880 
v = 0.88 v
th
R
C
3
v
o
s
4.3 k 
-
100 k 
Simplified ac equivalent circuit
R
B
th
C
+
+
v
g v
m be
v
th
be
r
r
-
R
R
C
vo
3
E
AC equivalent circuit with the bipolar transistor replaced by its small-signal model
R
th
v
v
th
+
+
be
r
g v
m be
R
L
v
-
Final equivalent circuit for ac analysis of the common-emitter amplifier
o
-