capitolo i - Sistema ETD

II Giunzione Tunnel Singola
Equation Section 2
Considerando da un punto di vista classico una giunzione tunnel metallo/isolante/metallo, non
si prevede alcun passaggio di carica attraverso l'isolante, ed essa si comporta come un condensatore di
capacità C.
La carica Q sulla giunzione è una grandezza continua perchè è dovuta allo spostamento della nube
elettronica rispetto agli ioni positivi del reticolo: potrà quindi assumere un valore inferiore al quanto di
carica e. L'interazione tra le due distribuzioni di carica ai lati della giunzione è descritta da un'energia
Q2
di caricamento:
.
2C
Dal punto di vista quantistico, si deve considerare il tunneling di elettroni, quindi di carica
discreta, attraverso la giunzione: il cambiamento di energia che coinvolge la giunzione a seguito di un
fenomeno di tunneling è dell'ordine dell'energia di caricamento:
Ec 
e2
2C
Perchè sia sensato parlare di effetti di caricamento, questi non devono esser mascherati da
fluttuazioni termiche,per cui la nostra ipotesi di lavoro sarà:
Ec
K BT
Tale condizione richiede una temperatura di lavoro e una capacità di giunzione (e quindi le dimensioni
della giunzione stessa) molto basse: ad esempio, una giunzione di 100 100nm 2 ed un ossido spesso
10 ha una capacità di 1fF, che corrisponde ad una temperatura di T=1K.
Presentiamo ora due diversi comportamenti della singola giunzione tunnel.
II.1 Visione Globale e Locale
Si consideri una giunzione tunnel connessa ad un generatore ideale di tensione V: la carica
sulla giunzione tunnel è quindi mantenuta fissa ad ogni istante.
Dopo calcoli di cui ci limitiamo a giustificare intuitivamente il risultato, si ottiene per la
relazione tensione-corrente:
I V  
1
eRT

 f  E  1  f  E  eV   f  E  eV  1  f  E  dE
(II.1)

1
è la distribuzione di Fermi-Dirac alla temperatura T. Il primo termine
 E 
1  exp 

 K BT 
fornisce la probabilità di trovare un elettrone di energia E nella parte sinistra ed un corrispondente stato
vuoto in quella destra.
Il dislivello tra i livelli di Fermi dei due lati della giunzione viene considerato nel termine eV
nell'argomento della seconda Fermi-Dirac. Il secondo termine è analogo al primo, ma descrive il
processo inverso.
Ove f  E  
15
ELEMENTI DI ELETTRONICA A SINGOLO ELETTRONE
Calcolando esplicitamente l'integrale (II.1), si trova che esso è indipendente dalla temperatura e
può essere riscritto come:
I
V
RT
La caratteristica tensione-corrente di questo sistema è dunque la stessa di un resistore ohmico:
chiameremo d'ora in avanti RT resistenza di tunneling, ben coscienti però del meccanismo di
conduzione molto diverso attraverso una giunzione tunnel ed un resistore.
Si consideri ora una giunzione tunnel polarizzata da una corrente I costante e misuriamo la
caduta di tensione ai suoi capi con un voltmetro ad alta impedenza: l'effetto di un evento di tunneling è
che Q, continua, diminuisca della quantità discreta e.
Si trova facilmente che la diminuzione di energia elettrostatica della giunzione in seguito al tunneling
di un elettrone è:
e

eQ  
2
Q

e
   2
Q 
i
E  E    E f 

2c
2C
C
2
A T=0K il tunneling si potrà verificare solo se E è positivo, ovvero se porta una diminuzione
dell'energia della giunzione.
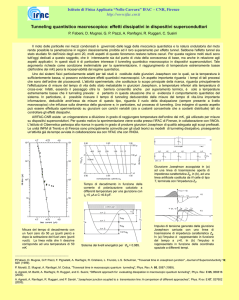
Fig. 1: Diagramma di energia che illustra l'origine del Coulomb Blockade del tunneling di un singolo elettrone in una
giunzione polarizzata da un generatore di corrente. Le transizioni favorevoli dal punto di vista energetico sono
rappresentate con linee continue, quelle sfavorevoli con linee tratteggiate.
Se consideriamo la caratteristica I-V della giunzione,essa avrà un ramo:

e
e
V 
2C
2C
per I=0. Questo è il Coulomb blockade per singole giunzioni.
Imponendo una corrente costante attraverso la giunzione, Q cresce linearmente col tempo per il
e
progressivo accumularsi della carica fornita dalla corrente finchè, raggiunto il valore di soglia , non
2
e
si verifica un evento di tunneling che la riporti a  : a questo punto si innesca un altro ciclo.
2
16
Q dunque avrà un andamento temporale a dente di sega, con frequenza di oscillazione:
f SET 
I
e
Come si vede, si è stabilita una correlazione temporale, o autocorrelazione, degli eventi di tunneling:
questo fenomeno prende il nome di SET (Single Electron Tunneling) oscillation.
Fig. 2: (a)Giunzione tunnel singola polarizzata da una corrente I. (b)Successione degli eventi di tunneling nel processo
della SET oscillation.
In alternativa al generatore ideale di corrente si può usare anche un generatore di tensione per
fornire corrente alla giunzione attraverso una resistenza alta, che sia minore della resistenza di
tunneling, ma abbastanza grande perchè impedisca una veloce ricarica della capacità dopo un evento di
e
tunneling. Per quanto suddetto non scorrerà corrente nel circuito se la tensione fornita è 
.A
2C
e
1
temperatura T=0K la caratteristica è una retta di pendenza
spostata in tensione di
, detto
2C
RT
Coulomb Gap.
In quest'ultimo caso, la variazione di energia associata all'evento di tunneling è la diminuzione
nell'energia di caricamento della giunzione che si registra quando questo si verifica. Si parla quindi di
visione locale: si è infatti presa in considerazione solo la giunzione ignorando le sue interazioni con
l'ambiente.
Nel primo caso invece si è adottata una visione globale del circuito. Dopo un evento di
tunneling infatti si crea una situazione di non equilibrio in cui la carica Q  e presente sulla giunzione
e la carica Q imposta dal generatore di tensione sono diverse. Per ristabilire l'equilibrio il generatore
deve trasferire un elettrone che riporti la carica sulla giunzione al valore originario Q . Quindi non c'è
alcun cambiamento nell'energia di caricamento: si deve però tener conto del lavoro eV compiuto dal
generatore in seguito al trasferimento di carica che è chiamato a realizzare.
A questo punto è normale chiedersi quale delle due descrizioni sia corretta. La soluzione al
problema può esser trovata non trattando la singola giunzione come disaccoppiata dall'ambiente,
connettendola ad un generatore ideale di tensione o di corrente, ma solo considerando l'influenza
dell'ambiente elettromagnetico.
17
ELEMENTI DI ELETTRONICA A SINGOLO ELETTRONE
Seguendo questo approccio si troverà che le visioni globale e locale non sono che casi limite di
un modello più generale.
II.2 Teoria della Singola Giunzione
Prima di presentare un'analisi dell'influenza dell'ambiente elettromagnetico della giunzione
sulla probabilità di tunneling, si devono considerare i tempi caratteristici del problema.
Il primo tempo caratteristico è l'inverso della frequenza di tunneling per una giunzione
e
polarizzata da un generatore ideale di tensione di valore V  :
C
 r  RT C
che è il tempo maggiore.
Il tempo intermedio è il tempo di rilassamento del sistema, che intercorre tra un evento di
tunneling ed il raggiungimento dello stato stazionario:
c 
hC
 RK C
e2
h
è il quanto di resistenza.
e2
Infine, il tempo più breve è quello di tunneling  t , che può esser pensato come quello trascorso
dall'elettrone dentro la barriera.
Si deve a questo punto modellare l'ambiente elettromagnetico della giunzione, che include non
solo la strumentazione per la misurazione della caratteristica I-V, di solito a temperatura ambiente, ma
anche i fili vicino alla giunzione.
ove RK 
II.2.1
Descrizione dell’ambiente
Si considera la risposta dell'ambiente fino alla frequenza di cut-off  t 1 : tale frequenza è
caratteristica del dominio ottico, ma la giunzione può esser considerata come un elemento concentrato,
avendo dimensioni submicrometriche (per assicurare una capacità dell'ordine dei fF).
Assumendo che l'ambiente sia lineare, la circuiteria di polarizzazione, che comprende
l'elettronica a temperatura ambiente, i filtri ed i fili fino ai pads del chip della giunzione, può essere
schematizzata da un generatore di tensione ideale Vb con una resistenza Rb in serie ed un condensatore
cb in parallelo che modella le capacità parassite della circuiteria di polarizzazione. Questi elementi
tengono conto della risposta per basse frequenze dell'ambiente, e sono in serie ad un'impedenza
complessa Z   che tiene conto invece del comportamento per alte frequenze (fig.1(a)).
Fig. 1: Modello a parametri concentrati dell'ambiente elettromagnetico visto da una giunzione tunnel di capacità C e
resistenza di tunneling RT
Osservando poi che Cb è di solito almeno 104 C , si capisce come il cambiamento della tensione
su di esso causato da un evento di tunneling sia in pratica trascurabile e quindi il modello possa essere
18
semplificato: otterremo così un'impedenza Z   in serie ad un generatore ideale di tensione
V  Vb  Rb I V  (fig.1(b)).
A questo punto lo scopo è stabilire quali valori dovrà
assumere Z   alle frequenze
caratteristiche della giunzione per osservare il Coulomb Blockade.
Frequenza di Tunneling
II.2.2
Il trasferimento di cariche attraverso la giunzione tunnel sarà caratterizzato da una frequenza di
tunneling diretto (ovvero dall'elettrodo 1 all'elettrodo 2)  ed una di tunneling inverso (da 2 a 1)  .
L'ipotesi centrale di questa teoria è una definita proporzione tra i tempi caratteristici della
giunzione:
t
c
r
La prima diseguaglianza equivale a considerare il tempo di tunneling trascurabile, mentre la
seconda, che implica:
RT
RK
permette di assumere che prima di un evento di tunneling il sistema giunzione tunnel-ambiente
elettromagnetico abbia raggiunto uno stato di equilibrio ad una tensione V che cade sulla giunzione ed
una temperatura del sistema pari a T. Il livello di Fermi dell'elettrodo 1 starà quindi sopra quello
dell'elettrodo 2 di eV .
Stabilendo che una tensione positiva favorisca il passaggio di elettroni dall'elettrodo 1
all'elettrodo 2, si ottiene:
1
 V   2
e RT
 
  f  E  1  f  E P  E  eV  E  dEdE
'
'
'
(II.2)
 
E è l'energia posseduta dall'elettrone quando si trova sull'elettrodo 1 ed E ' è la sua energia
finale sull'elettrodo 2, entrambe misurate rispetto ai livelli di Fermi.
Data la:
Re  Z t    
 
coth 
 RK
 2 K BT



J t   2 


 cos  t   1  j sin  t   d


ove:
Zt   
1
jC  Z 1  
che è detta funzione di correlazione, la P  E  sarà la sua trasformata continua di Fourier:

1
jEt 

P  E    exp  J  t  
dt
h 

19
ELEMENTI DI ELETTRONICA A SINGOLO ELETTRONE
È chiaro dunque che si potrà
calcolare la P  E  per il nostro circuito solo dopo che
l'impedenza esterna sia nota. In genere non è possibile calcolare P  E  analiticamente, eccetto casi
particolari.
P  E  possiede comunque proprietà generali che non dipendono dall'impedenza Z   :

 P  E  dE  1
(P.1)


 EP  E  dE  E
c
(P.2)

 E 
P   E   exp  
 PE
 K BT 
(P.3)
Per capire il significato fisico di P  E  i deve osservare che, se non ci fossero interazioni
energetiche tra la giunzione ed il circuito esterno, si avrebbe allora E  eV  E ' .
La (P1) suggerisce di pensare la P  E  come una probabilità: essa sarà dunque la probabilità
che un elettrone ceda l'energia E al circuito esterno. Per $E<0,$ P  E  rappresenta la probabilità di
assorbimento dell'energia E da parte dell'elettrone che sta facendo tunneling.
Si noti infine che, dalla (P3), a temperatura T=0K, P  E  si annulla per energie negative: non
può esistere dunque assorbimento di energia dall'ambiente.
Alla luce di queste considerazioni, l'espressione di  V  , che discende da una trattazione
quantistica del sistema qui completamente omessa, può quantomeno essere giustificata intuitivamente
osservando che è legata alla probabilità di trovare un elettrone (uno stato occupato) di energia E  EF 1
sull'elettrodo 1, a quella di trovare uno stato vuoto di energia E '  EF 2 sull'elettrodo 2 ed a quella che
l'elettrone ha di scambiare con il circuito esterno una quantità di energia pari al salto energetico che
deve compiere quando fa tunneling.
Manipolando opportunamente (II.2), si ottiene l'espressione equivalente:
1
 V   2
e RT



E
 E 
1  exp  

 K BT  

P  eV  E  dE
Per la frequenza di tunneling inversa si ottiene poi:
 V     V 
com'era ovvio data la simmetria del problema.
In virtù della (P3) si ottiene infine:
 eV 
 V   exp  
  V 
 K BT 
20
Caratteristica tensione-corrente
II.2.3
Ammesso che la corrente attraverso la giunzione sia I
e
, essa sarà semplicemente pari alla
c
carica che passa durante un evento di tunneling per la differenza tra le frequenze di tunneling diretto e
inverso. Essa sarà quindi espressa da:
I V   e  V    V   

 eV  
1

exp




1
 K BT  


P  eV  E  dE
E
eRT 
 E 
1  exp  

 K BT  

(II.3)
Che permette di determinare la caratteristica I-V per qualsiasi temperatura e qualunque sia il
comportamento dell'ambiente elettromagnetico al variare della frequenza.
Per alte tensioni, tali che eV K BT , la (II.3) diventa:
I V  
1
eRT


EP  eV  E  dE 

1
eRT

  eV  E P  E  dE

che, per le (P1) e (P2), implica:
I V  
1 
e 
V 

RT 
2C 
Dunque la caratteristica I V  presenta un andamento ohmico, ma è spostata in tensione di
e
, il
2C
Coulomb Gap.
Specifichiamo ora la (II.2) nei due casi limite di ambiente a bassa ed alta impedenza.
Nel caso di bassa impedenza, ovvero Z   RK , si ha P  E    E  (e quindi non c'è
possibilità che un elettrone scambi energia con l'ambiente esterno), per cui si ottiene:
 V  
1
e RT
2
eV
 eV 
1  exp  

 K BT 
Dunque non si ha Coulomb Blockade. In questo caso infatti la corrente sarà esprimibile in funzione
della tensione come:
I V  
V
RT
Si ritrova quindi il risultato della visione globale del circuito, quando la giunzione era polarizzata da
un generatore ideale di tensione: nell'approssimazione di bassa impedenza infatti si può porre
Z   ~ 0 .
21
ELEMENTI DI ELETTRONICA A SINGOLO ELETTRONE
Nel caso di alta impedenza, ovvero per Z  
RK per    c 1, si ottiene un andamento
gaussiano:
  E  Ec 2 
1
PE 
exp  

4 Ec K BT
 4 Ec K BT 
A temperatura T=0K P  E    E  Ec  (per cui un elettrone può fare tunneling quando cede
un'energia Ec all'ambiente esterno) per cui la (II.2) diventa:
 V  
1
 eV  Ec  H  eV  Ec 
e RT
2
Ove H(x) è la funzione di Heavside. Questo risultato descrive il Coulomb Blockade del tunneling,
e
perchè come si vede  V  diventa 0 per V 
: se, infatti, un elettrone che fa tunneling trasferisce
2C
sempre un'energia pari a Ec all'ambiente elettromagnetico, perchè tale transizione abbia luogo
l'energia a disposizione eV deve superare Ec . Si è quindi ritornati alla visione locale del circuito: la
connessione si fa più chiara se si nota che:
Q2 Q  e 
eV  Ec 

2C
2C
2
BIBLIOGRAFIA
“Electrical Conduction Mechanism in Ultrathin, Evaporated Metal Films” C. A. Neugebauer, M. B. Webb, J.
Appl. Phys. 33,74 (1962)
''Single electron tunneling rates in multijunction circuits'' H. Grabert, G. L. Ingold, M. Devoret, D.Estève, H.
Pothier, C. Urbina Z. Phys. B-Condensed Matter 84, 143 (1991)
''Effect of the Electromagnetic Environment on the Coulom Blockade in Ultrasmall Tunnel Junctions''M. Devoret,
D.Estève, H. Grabert, G. L. Ingold, H. Pothier, C. Urbina Phys. Rev. Lett. 64, 1824 (1990)
''Finite-Temperature Current-Voltage Characteristcs of Ultasmall Tunnel Junctions'' G. L. Ingold, H.\ Grabert
Europhys. Lett. 14, 371 (1990)
''Introduction to single charge tunneling'' M. H. Devoret, H. Grabert in ''Single charge tunneling'', M. H. Devoret,
H. Grabert, eds. New York: Plenum (1992)
''Charge tunneling rates in ultrasmall junctions'', G. L. Ingold, Yu. V. Nazarov in''Single charge tunneling'', M. H.
Devoret, H. Grabert, eds. New York: Plenum (1992)
''Effect of High-Frequency Electrodynamic Environment on the Single-Electron Tunnelig in Ultrasmall Junctions''
P. Delsig, K. K. Likharev, L.S. Kuzmin, T. Cleason, Phys. Rev. Lett. 63, 1180 (1989)
''Coulomb Blockade of Single Electron Tunneling, and Coherent Oscillations in Small Tunnel Junctions'', D. V.
Averin, K. K. Likharev, J. Low Temp. Phys. 62, 345 (1986)
1.
2.
3.
4.
5.
6.
7.
8.
1
Infatti la corrente che attraversa la giunzione dev' essere tale che:
I
e
c
perchè il modello sia significativo, per cui le frequenze d'interesse saranno necessariamente
sufficiente che
22
Z  
RK
nell’intervallo di

1
c
. Per parlare di alta impedenza d’ambiente è quindi