Problemi similitudine

SIMILITUDINE
Problemi
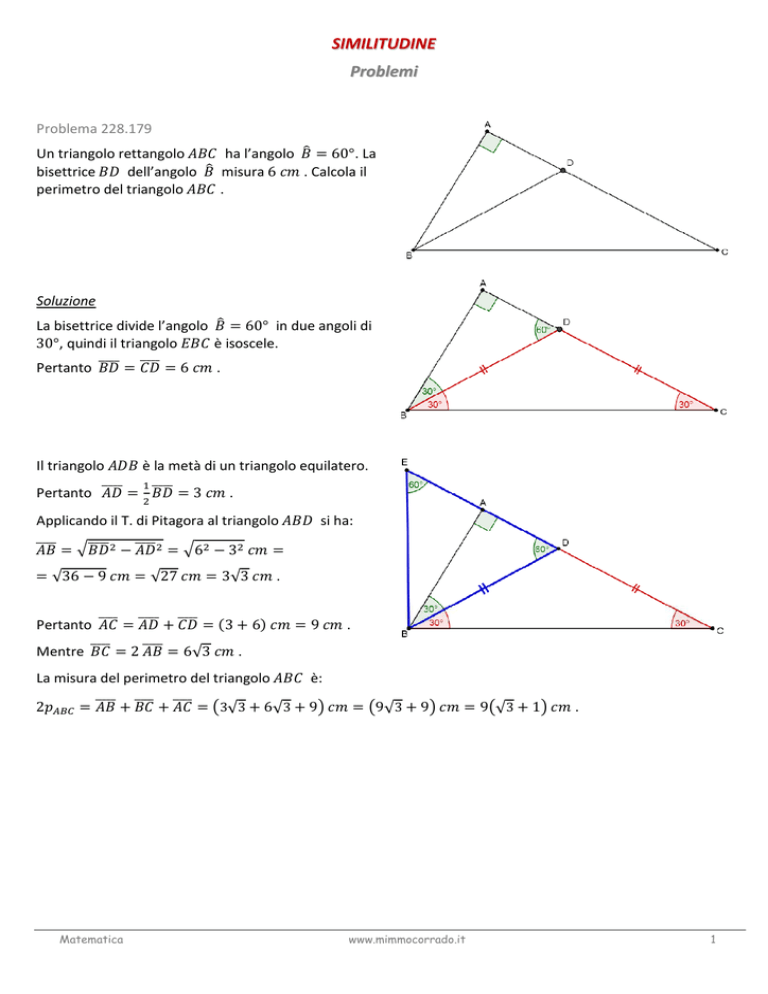
Un triangolo rettangolo ha l’angolo = 60°. La
bisettrice dell’angolo misura 6 . Calcola il
perimetro del triangolo .
Problema 228.179
La bisettrice divide l’angolo = 60° in due angoli di
30°, quindi il triangolo è isoscele.
Soluzione
= 6 .
= Pertanto Il triangolo è la metà di un triangolo equilatero.
= Pertanto = 3 .
Applicando il T. di Pitagora al triangolo si ha:
= = 6 − 3 =
− = √36 − 9 = √27 = 3√3 .
= + = 3 + 6 = 9 .
Pertanto = 6√3 .
= 2 Mentre La misura del perimetro del triangolo è:
+ + = 3√3 + 6√3 + 9 = 9√3 + 9 = 9√3 + 1 .
2 = Matematica
www.mimmocorrado.it
1
= 12 = 16 , , "
# = 90° .
Nel triangolo rettangolo raffigurato a lato, " = "
Calcola l’area del triangolo $".
Problema 228.136
Applicando il T. di Pitagora al triangolo si ha:
Soluzione
= + = 16 + 12 =
= √256 + 144 = √400 = 20 = 10 .
Pertanto " = "
I triangoli e " sono simili. Infatti:
L’angolo è in comune
# perché entrambi retti.
' ≅ "
= "
;
∶ " ∶ Pertanto hanno i lati corrispondenti in proporzione:
10 ∶ 16 = " ∶ 12 ;
10 ∙ 12
15
=
16
2
1
1
15
75
∙ "
= / ∙ 10 ∙ 0 =
∙ "
2
2
2
2
In definitiva l’area vale:
,-. =
=
"
Matematica
www.mimmocorrado.it
2
= 9 , = 12 e "1
# = 90° . Calcola il
Nel triangolo rettangolo raffigurato a lato, perimetro del triangolo "1.
Problema 228.140
Applicando il T. di Pitagora al triangolo si ha:
Soluzione 1
= + = 9 + 12 =
= √81 + 144 = √225 = 15 L’area del triangolo è:
1
1
∙ = ∙ 9 ∙ 12 = 54 ∙ 2
2
L’altezza relativa all’ipotenusa misura:
, =
=
"
2 ∙ , 2 ∙ 54
36
=
=
15
5
Applicando il T. di Pitagora al triangolo " si ha:
− "
= = 312 − 4568 = 3144 − 96 = 35:; = ;< .
"
7
7
7
7
Inoltre i triangoli e "" sono simili. Infatti:
L’angolo ' è in comune
# perché entrambi retti.
' ≅ "1
= "
∶ ;
∶ "1
Pertanto hanno i lati corrispondenti in proporzione:
48
5 = 9 ∙ 48 ∙ 1 = 144 ∶ 9 =
=
"1
∶ 15 ;
"1
5
15
5 15
25
Applicando il T. di Pitagora al triangolo "1 si ha:
9∙
48
= "
− "1
= 34568 − 4;;8 = 396 − :=56 = 35;::>:=56 = 366; = :< 1
7
7
7
67
67
67
7
La misura del perimetro del triangolo "1 è:
+ "1
= /
+ 1
2-. = "
36 144 108
180 + 144 + 108
432
+
+
0 =
=
.
5
25
25
25
25
Dopo aver determinato le misure dell’ipotenusa e dell’altezza relativa all’ipotenusa " , si sfrutta la
similitudine dei triangoli e "1 :
Soluzione 2
∶ = "1
;
∶ "
36
36 1
144
= 12 ∙
: 15 = "1 ∶ 12 ;
"1
∙
=
5
5 15
25
.
Si calcola in seguito, con il T. di Pitagora, la misura di 1
Matematica
www.mimmocorrado.it
3
In un triangolo rettangolo , di cateti 16 e 12 , traccia l’altezza " relativa all’ipotenusa e la
bisettrice 1 dell’angolo retto. Calcola l’area del triangolo "1.
Problema 292.202
Applicando il T. di Pitagora al triangolo si ha:
Soluzione
= + = 12 + 16 =
= √400 = 20 L’area del triangolo vale:
∙ = 4 ∙ 12 ∙ 168 = 96 .
, = 2 ∙ , 2 ∙ 96
48
=
=
.
20
5
L’altezza relativa all’ipotenusa misura:
=
"
Ricordando il T. della bisettrice:
“La bisettrice di un angolo interno di un triangolo divide il lato opposto in parti direttamente proporzionali agli altri due
lati”,
∶ ∶ 1
1 = ∶ 1
1 = 12 ∶ 16 ;
si ottiene:
= A
Ponendo 1
⇒
= 12 ∶ 16 ;
A ∶ 1
+ 1
= 20
Considerando che: 1
4
A + A = 20 ;
3
si ha:
3A + 4A = 60 ;
7A = 60 ;
= ; ∙ 6: = <: .
= 60 e 1
Pertanto 1
7
5 =
=
Applicando il T. di Pitagora al triangolo " si ha:
= 6C = ; A .
1
5
A=
60
7
= − "
= 312 − 4;< 8 = 3144 − 5:; = 396 = 56 .
"
7
7
7
7
− "
= 4 − 8 =
= 1
Si ricava quindi: "1
7
7
60
56
5::>7
57
1 48 48
1152
1
= / ∙
,-. = "1 ∙ "
∙ 0 =
2 35 5
175
2
= 57 .
;<
In definitiva l’area vale:
Matematica
www.mimmocorrado.it
4
= 16 e altezza Un rettangolo di perimetro 28 è inscritto in un triangolo di base " = 12 .
Calcola le dimensioni del rettangolo.
Problema 294.217
I triangoli e sono simili. Infatti:
L’angolo ' è in comune
# perché corrispondenti ….
' ≅ ≅ perché corrispondenti ….
Soluzione
Ricordando il teorema:
“In due triangoli simili le basi sono proporzionali alle rispettive altezze”
∶ ∶ 1
= "
si ha:
= A
Ponendo D
⇒
= "
− D
= 12 − A
1
16 ∶ 14 − A = 12 ∶ 12 − A ;
12 ∙ 14 − A = 16 ∙ 12 − A ;
= 14 − A
168 − 12A = 192 − 16A ;
−12A + 16A = 192 − 168 ;
4A = 24 ;
A =6.
= 6 è Pertanto D
= 8 .
Matematica
www.mimmocorrado.it
5
In una circonferenza di centro E inscrivi un triangolo isoscele avente la base di 16 e i lati obliqui di 20 ciascuno. Calcola la misura del raggio.
Problema 206.113
= 8 2
Applicando il T. di Pitagora al triangolo " si ha:
Soluzione 1
=
"
− "
= 20 − 8 = √336 = 4√21 " = Applicando il I T. di Euclide al triangolo si ha:
= "
∙ ;
=
400
4√21
=
100
=
√21
Pertanto il raggio misura:
F=
50 √21
=
.
2
21
;
20 = 4√21 ∙ 100 √21
21
100 √21
∙
=
.
21
21
√21 √21
Soluzione 2
∶ ∶ HD
;
CH
AH = HB
Applicando il T. delle corde si ha:
HD =
8∙8
4√21
Pertanto:
=
16
√21
=
16
∙
√
√21
√21 √21
√
=
4√21 ∶ 8 = 8 ∶ HD
16 √21
21
16 √21
84√21 + 16 √21
100√21
4√21 + 21
50 √21
" + "
21
21
=
=
=
=
.
F =
2
2
2
2
21
Matematica
www.mimmocorrado.it
6
Due corde AB e CD di una circonferenza di raggio 10 si intersecano in un punto $ interno a essa. Sapendo
= 7cm e le parti un cui è divisa CD sono lunghe 6 e 2 , determina le lunghezze delle parti in
che AB
cui è divisa la corda AB.
Problema 206.116
= A
Ponendo $
= 7 − A
⇒ $
Soluzione
Applicando il teorema delle corde si ha:
$: $ = $: $
6 ∶ A = 7 − A ∶ 2 ;
A ∙ 7 − A = 6 ∙ 2 ;
7A − A = 12 ;
A − 7A + 12 = 0 ;
A = 3
A = 4
= 3 e $
= 4 .
Pertanto $
Da un punto $ esterno a una circonferenza e distante 20 dal centro E di essa, conduci una tangente
lunga 12 cm . Determina la lunghezza del raggio.
Problema 206.117
Applicando il T. di Pitagora al triangolo $E si ha:
Soluzione 1
= E$
− $
= 20 − 12 =
F = E
= √400 − 144 = √256 = 16 .
= A
Ponendo E
Soluzione 2
⇒
∶ $ ∶ $ = $
$ ;
= 20 − A e $
= 20 + A
$
Applicando il T. della tangente si ha:
20 + A ∶ 12 = 12: 20 − A
20 + A ∙ 20 − A = 12 ∙ 12 ;
400 − A = 144 ;
A = 256 ;
A = ∓√256 = ∓16 .
Scartando la soluzione negativa si ha: F = E = 16 .
Matematica
www.mimmocorrado.it
7
L’area di un triangolo rettangolo è 80 e l’ipotenusa è lunga 20 . Calcola la misura dei cateti.
Problema 214.173
Soluzione 1
2 , 2 ∙ 80
=
= 8 .
20
I triangoli " e " sono simili. Infatti:
L’altezza relativa all’ipotenusa misura:
" =
# ≅ "
# ≅ 90° .
"
' " ≅ 90° − "' ≅ ∶ ∶ "
" = "
"
= A e Ponendo "
" = 20 − A si ottiene:
Pertanto i lati corrispondenti sono proporzionali:
A ∶ 8 = 8 ∶ 20 − A ;
A − 20A + 64 = 0 ;
A ∙ 20 − A = 8 ∙ 8 ;
= 4 Pertanto "
∆
= 10 − 64 = 36 ;
4
= 16 .
"
Applicando il T. di Pitagora al triangolo " si ha:
e
20A − A = 64 ;
A, = 10 ∓ 6 =
A = 4
A = 16
= = 8 + 4 = √64 + 16 = √80 = 4√5 " + "
Applicando il T. di Pitagora al triangolo " si ha:
= = 8 + 16 = √64 + 256 = √320 = 8√5 " + "
Soluzione 2
2 , 2 ∙ 80
=
= 8 .
20
= A ⇒ Ponendo "
" = 20 − A
L’altezza relativa all’ipotenusa misura:
" =
Applicando il II T. di Euclide al triangolo si ha:
∙ "
;
" = "
8 = A ∙ 20 − A ;
A − 20A + 64 = 0 ;
= 4 Pertanto "
∆
= 10 − 64 = 36 ;
4
= 16 .
"
64 = 20A − A ;
A, = 10 ∓ 6 =
Applicando il T. di Pitagora al triangolo " si ha:
e
A = 4
A = 16
= = 8 + 4 = √64 + 16 = √80 = 4√5 " + "
Applicando il T. di Pitagora al triangolo " si ha:
= = 8 + 16 = √64 + 256 = √320 = 8√5 " + "
Matematica
www.mimmocorrado.it
8
= 10 , = 15 , Nel triangolo isoscele raffigurato a lato, = 5 Problema 215.180
e ∥ . Calcola il perimetro e l’area del triangolo CLM.
Il perimetro del triangolo misura:
Soluzione
+ = 10 + 15 + 15 = 40 + 2 = Applicando il T. di Pitagora al triangolo " si ha:
− "
= √225 − 25 = √200 = 10√2 " = L’area de triangolo vale:
∙ "
= 4 10 ∙ 10√28 = 50√2 .
, = I triangoli e " sono simili. Infatti:
' è in comune
# perché angoli corrispondenti fra DE ∥ AB tagliate da AC
#E ≅ A
CD
≅ perché angoli corrispondenti fra ∥ tagliate da Ricordando il teorema:
“Il rapporto fra i perimetri di due triangoli simili è uguale al rapporto fra le misure dei lati corrispondenti”,
si ottiene:
2
∶ ;
∶ 2 = 40 ∶ 2 = 15 ∶ 5
Ricordando il teorema:
2
=
40 ∙ 5
40
=
.
15
3
“Il rapporto fra le aree di due triangoli simili è uguale al rapporto fra i quadrati delle misure dei lati
corrispondenti”, si ha:
,UV
=
;
,
,UV =
,UV
5
= ;
15
50√2
50
√2 2 .
9
,UV
50√2
=
25
;
225
,UV
50√2
=
1
;
9
Problema 215.181
Un rettangolo il cui perimetro è 15a è simile a un altro rettangolo la cui base è 8a e la cui altezza è 2a. Calcola
la misura dei lati e l’area del primo rettangolo.
Il perimetro del rettangolo W X è
Soluzione
YZ = 2 ∙ 8[ + 2[ = 20[
Essendo i due rettangoli W e W X simili, si ha che i perimetri sono proporzionali ai lati corrispondenti:
Y ∶ YZ = \ ∶ \ X
15[ ∶ 20[ = \ ∶ 8[
L’altezza ℎ =
7
Matematica
\=
7] ∙ <]
:]
= 6[ .
[ − 6[ = [ . L’area del rettangolo W è: , = \ ∙ ℎ = 6[ ∙ [ = 9[ .
5
da cui si ottiene:
www.mimmocorrado.it
5
9
Problema 215.184
Il lato AB di un triangolo ABC misura a. Conduci da un punto P di AB la parallela PQ a un altro lato in modo che
il triangolo risulti suddiviso in due poligoni equivalenti.
= A
Poniamo $
Soluzione 1
Con i limiti geometrici: 0 < A < [
I due triangoli $`
perché:
e
sono simili
l’angolo ' è in comune
` $ ≅ ' (angoli corrispondenti)
$ ` ≅ (angoli corrispondenti)
Pertanto i due triangoli $` e hanno i lati proporzionali alle altezze corrispondenti:
∶ = `"
∶ 1
$
∶ 1
;
A ∶ [ = `"
L’equivalenza fra il triangolo $`
e il trapezio `$
$` ≗ `$ In simboli:
⇔
Sostituendo i dati conosciuti si ha:
∙.
= 2∙
∙d
c
;
= 2 ∙ A ∙ C 1
;
[ ∙ 1
]
A
[ =2∙
;
[
A = ∓3
[
=∓
√
[=
√
∓ [
A = −
A =
⇔
√
[
√
+[
= C `"
1
]
l’area del triangolo ABC è il doppio
dell’area del triangolo $`
∙ 1
= 2 ∙ $
∙ `"
;
[ = 2A ;
=
⇔
≗ 2 ∙ $`
≠ 0
dividendo per 1
da cui si ottiene:
, = 2 ∙ ,cd
si ottiene:
[
A =
;
2
fgf [hii[\jkh
[hii[\jkh
Soluzione 2
Ricordando il teorema:
“Il rapporto fra le aree di due triangoli simili è uguale al rapporto fra i quadrati delle misure dei lati
corrispondenti”, si ha:
∶ $
= , ∶ ,cd ;
[ ∙ ,cd
A =
2,cd
A = ∓3
[
;
=∓
Matematica
√
[=
√
∓ [
[ ∶ A = 2 ,cd ∶ ,cd ;
=
A = −
A =
√
[
√
+[
A =
1 [ ;
2
fgf [hii[\jkh
[hii[\jkh
www.mimmocorrado.it
10
Considera una circonferenza avente il raggio di 3 e circoscrivi a essa un triangolo isoscele sulla base
6
. Il rapporto tra l’altezza " e la base è . Determina le lunghezze dei lati del triangolo.
Problema 215.191
7
Soluzione
= A
Poniamo "
= 6 2A = A
"
=
E
7
7
⇒
7
A−3
= 2A
= 3;; A + A = 369 A = 5 A .
7
7
7
Dalla similitudine dei triangoli E e " si ottiene:
∶ = E
∶ E
" ;
39
12
A = A ∙ / A − 30 ;
5
5
A=0
9
2A − 9A = 0 ;
A=
2
Pertanto:
12
13
A − 30 ∶
A=3∶A
5
5
39
12 A=
A − 3A ;
5
5
/
12A − 54A = 0 ;
9
= 9 2
13 9 117
=
∙ =
= 11,7 .
5 2
10
= 2 ∙
Matematica
www.mimmocorrado.it
11
Problema 215.192
É dato un triangolo rettangolo il cui cateto è 12 . Si sa, inoltre, che il cateto è di .
;
Determina su un punto $ in modo tale che, detta ` la sua proiezione ortogonale su , sussista la
+ 2$`
= 40$
− 3 .
relazione: $
5
Soluzione
3
∙ 12 = 9 4
Calcoliamo innanzitutto le misure degli altri due lati:
=
= 12 + 9 = √144 + 81 = √225 = 15 = A ⇒ Indicando: $
$ = 12 − A
geometrici 0 < A < 12 .
con i vincoli
Dalla similitudine dei due triangoli e $` (l’angolo in comune e ' = $` = 90°) si ottiene:
∶ = $
;
∶ $`
∶ 9 = 12 − A ∶ 15 ;
$`
=
$`
= $
;
∶ ∶ `
∶ 12 = 12 − A ∶ 15 ;
`
=
`
Mentre
4
75 − 48 + 4A 27 + 4A
= − `
= 15 − 12 − A =
`
=
5
5
5
Applicando il T. di Pitagora al triangolo rettangolo CPQ si ricava:
Pertanto:
9 ∙ 12 − A 3
= 12 − A .
15
5
12 ∙ 12 − A 4
= 12 − A .
15
5
3
27 + 4A 9
729 + 16A + 216A
= $`
+ `
= l 12 − Am + /
144 + A − 24A +
$
0 =
=
5
25
5
25
1296 + 9A − 216A + 729 + 16A + 216A 2025 + 25A =
=
= 81 + A .
25
25
= 40$
− 3 si ottiene:
Sostituendo le espressioni trovate nella relazione: $ + 2$`
81 + A + 2 ∙
9
144 + A − 24A = 40A − 3 ;
25
Da cui si ricavano le radici: A = 2 e A = − 59 .
=<
Pertanto il punto P si trova a 2 dal vertice .
Di queste radici soltanto quella positiva è accettabile.
Matematica
www.mimmocorrado.it
12
Un rettangolo ha la superficie di 80 . Se si aumentano le sue dimensioni ciascuna di 2 , l’area aumenta
di 46 . Calcola la misura delle dimensioni.
x
2
Problema 215.193
y
Soluzione
Ponendo le dimensioni del rettangolo uguali a A e n.
Si ottiene il sistema:
A ∙ n = 80
o
A + 2n + 2 = 80 + 46
80
A
p
q
80
80
A∙
+ 2A + 2 ∙
= 122
A
A
n=
80
p
on = A
2A − 42A + 160 = 0
Da cui si ricava:
A,
80
n=
p
o
A
An + 2A + 2n + 4 = 126
q
n=
80
A
80 + 2A +
p
160
− 122 = 0
A
80
p
on = A
A − 21A + 80 = 0
21 ∓ √441 − 320 21 ∓ 11 A = 5
=
=
=
A = 16
2
2
2
80
n=
p
o
A
An + 2A + 2n = 122
80
p
on = A
80A + 2A + 160 − 122A = 0
A = 5 p
n = 16
A = 16p
r n = 5
r
Le dimensioni del rettangolo sono pertanto: \ = 16 e ℎ = 5 .
Matematica
www.mimmocorrado.it
13
Stabilisci se si può inscrivere un trapezio isoscele che ha il perimetro di 20 in una semicirconferenza di
raggio 5 .
Problema 215.194
Soluzione
La base del trapezio deve coincidere con il diametro.
= 10 .
Pertanto + DC
+ CD
= 10 .
Quindi: AD
Cioè:
+ CB
= 5 . Ma ciò non può sussistere.
EC
Infatti, ricordando che:
la somma di due qualsiasi lati di un triangolo è maggiore del terzo
+ CB
> EB
= 5 .
> OB
si ha che: EC
in un triangolo rettangolo l’ipotenusa è maggiore di ciascuno cateto
Matematica
www.mimmocorrado.it
14
Problema 215.195
Un trapezio isoscele è circoscritto a
un semicerchio di raggio F. Sapendo
che la base minore è parallela al
5
diametro ed è lunga F, determina il
;
perimetro e l’area del trapezio.
Soluzione
Essendo = ; F
5
⇒
5
= < F
E ≅ E' perché alterni interni
e
5
E" = < F
E' ≅ E' u perché CE e CF sono tangenti alla circonferenza.
⇒
Il che dimostra che il triangolo OBC è isoscele con E ≅ .
= A
Poniamo E
⇒
E ≅ E' u
= A − 5 F
"
<
Con i limiti geometrici: A > F
+ "
;
= "
Applicando il T. di Pitagora al triangolo rettangolo BCH si ha:
3 9
3
F + /A − F0 = A ;
F + A + F − FA = A ;
8
64
4
73 73 4
73
3
FA =
F ;
A=
F ∙
;
A=
F
4
64
64
3F
48
= =5 F e = 2 ∙ =5 F = =5 F
Pertanto ;<
;<
;
73 3
F − FA = 0 ;
64
4
+ + =
2 = + In definitiva il perimetro del trapezio è:
Mentre l’area è:
=5
;
F+
=5
;<
F+ F+
5
;
=5
;<
F=
+ ∙ "
= ∙ 4 F + F8 ∙ F = F .
, = ∙ ;
;
;<
Matematica
=5
5
9
5<
;<
F=
;
6
F.
www.mimmocorrado.it
15
Disegna un arco AB, quarta parte di una circonferenza di centro E il cui raggio 5 . Fissa su AB un punto $ e
+ 2$"
= 11 .
indica con " la sua proiezione sul lato E. Determina la misura di PH in modo che: $
Problema 215.196
Soluzione
Poniamo $" = A
$ = 11 − 2A
Con i limiti geometrici: 0 < A < 5
⇒
e
1 = 5 − A
Applicando il T. di Pitagora al triangolo rettangolo OPH si ha:
= 25 − A E"
+ $1
;
= $
1
Applicando il T. di Pitagora al triangolo rettangolo PAK si ha:
5 − A + 425 − A 8 = 11 − 2A ;
25 + A − 10A + 25 − A = 121 + 4A − 44A ;
4A − 34A + 71 = 0 ;
\
\ − 428 ∓ 3428 − [
17 ∓ √289 − 284 17 ∓ √5
=
.
[
4
4
Soluzioni entrambe accettabili, perché rispettano i limiti geometrici.
A, =
=
= 20 , individua un punto P in modo tale che 2$
= 3$
.
Su una semicirconferenza di diametro Problema 215.198
Soluzione
= A
Poniamo $
⇒
5
$ = A
Con i limiti geometrici: 0 < A < 20
+ $
= $
Applicando il T. di Pitagora al triangolo rettangolo ABP si ha:
A + ; A = 400 ;
9
4A + 9A = 1600 ;
13A = 1600 ;
= ;: √13 .
Soltanto la soluzione positiva è accettabile. Pertanto $
5
A =
6::
5
;
A = ∓ 5 √13
;:
= "
∙ Applicando il I° T. di Euclide al triangolo rettangolo ABP si ha: $
= c = 6:: ∙ = <: .
Da cui si ottiene: "
5
:
5
v
Matematica
www.mimmocorrado.it
16
Il raggio di una circonferenza di centro E è 10 . Conduci una corda e indica con " il piede della
perpendicolare condotta da E ad .. Trova a quale distanza dal centro E si deve tracciare la corda affinché
+ E"
= 22 .
sussista la relazione Problema 218.206
Soluzione
Poniamo E" = A
= 100 − A "
con i limiti geometrici: 0 < A < 10.
= 2100 − A ⟹
+ Sostituendo nella relazione E" = 22 si ottiene:
2100 − A + A = 22 ;
4100 − A = 484 + A − 44A ;
2100 − A = 22 − A
400 − 4A − 484 − A + 44A = 0 ;
5A − 44A + 84 = 0 ;
A,
14
22 ∓ √484 − 420 22 ∓ √64
64 22 ∓ 8 A =
=
=
=
=
5
[
5
5
A = 6
Matematica
www.mimmocorrado.it
17
Considera un segmento lungo 9 . Tra gli estremi e prendi un punto $ e costruisci, dalla stessa
parte, i due triangoli equilateri $ e $. Calcola quale distanza deve avere $ da affinché risulti:
,cU = ,cU .
Problema 218.207
Soluzione
= A
Poniamo $
= 9 − A
$
=
"
√3
A
2
con i limiti geometrici: 0 < A < 9 .
=
$"
=
1
A
2
√3
9 − A
2
=
$1
9−A
2
Sostituendo nella relazione: ,cU = ,cU si ottiene:
1
,U.- − ,c- − ,cU. = ,cU
2
1
1
1
1 1
∙ "1
− + "
− = ∙ ;
1
$" ∙ "
$1 ∙ 1
$ ∙ 1
2
2
2
2 2
1
∙ "1
− $1
− $"
∙ "
∙ 1
= ;
+ "
1
$ ∙ 1
2
A 9−A
A √3
9 − A √3
1
√3
√3
√3
9 − A = 9 − A ∙
9 − A ;
x 9 − A +
Ay ∙ / +
0− ∙
A−
∙
2
2
2
2
2
2 2
2
2
2
9√3 9 √3 √3
√3
9 − A =
9 − A ;
∙ −
A −
2 2
4
4
4
81√3 √3 √3
9 − A = 0 ;
−
A −
4
4
2
81√3 √3 √3
81 + A − 18A = 0 ;
−
A −
4
4
2
81√3 √3 81√3 √3 −
A −
−
A + 9√3A = 0 ;
4
4
2
2
81√3 − √3A − 162√3 − 2√3A + 36√3A = 0 ;
−3√3A + 36√3A − 81√3 = 0 ;
A − 12A + 27 = 0 ;
A, =
\
\ − 2 ∓ 3428 − [
[
=
6 ∓ √36 − 27
A =3
=6∓3= A = 9
1
Soltanto la soluzione positiva: A = 3 è accettabile.
= 3 .
Pertanto $
Matematica
www.mimmocorrado.it
18
Un quadrato ha l’area di 75[ . Inscrivi in esso un altro quadrato uD" la cui area sia 39[ . Calcola le
lunghezze di e di .
Problema 215.208
Soluzione
,U = 75[
,Vz{- = 39[
Poniamo = A
⇒
⇒
⇒
= 5√3[
u = √39[
= 5√3[ − A
con i limiti geometrici: 0 < A < 5√3[ .
= u
+ u
Applicando il T. di Pitagora al triangolo rettangolo EBF si ha:
5√3[ − A
+ A = √39[
2A − 10√3[A + 36[ = 0 ;
A, =
;
75[ + A − 10√3[A + A = 39[ ;
A − 5√3[A + 18[ = 0 ;
−\ ∓ √\ − 4[ 5√3[ ∓ √75[ − 72[ 5√3[ ∓ √3[ A = 2√3[
=
=
=
2[
2
2
A = 3√3[
Soluzioni entrambe accettabili.
Matematica
www.mimmocorrado.it
19
Un trapezio isoscele che ha la base maggiore di 28 , la minore di 10 e l’altezza di 12 , si deve
suddividere, mediante una parallela alle basi, in due trapezi aventi l’area uguale. Trova a quale distanza dalla
base minore si deve tracciare la parallela.
Problema 215.209
Soluzione
,U =
:|<
∙ 16 = 228 ⇒ ,UVz = 114 = A
Poniamo 1
con i limiti geometrici: 0 < A < 12 .
− = 9 2
= 1
∶ "
∶ Dalla similitudine dei triangoli ADH e DEK si ha: 1
" ;
=
"
= 5 A .
Da cui si ricava: 1
;
Sostituendo nella relazione: ,UVz = 114 si ottiene:
+ u
= 114 ;
∙ 1
2
3
20A + A = 228 ;
2
A, =
\
\ − 428 ± 3428 − [
[
∙ 1
+ = 228 ;
u
3A + 40A − 456 = 0 ;
=
∶ 9 = A ∶ 12
1
3
/10 + A + 100 ∙ A = 228 ;
2
−20 ± √400 + 1368 −20 ± √1768 −20 ± 2√442
=
=
.
3
3
3
Scartando la soluzione negativa, si ha:
1 =
−20 + 2√442
3
Matematica
www.mimmocorrado.it
20
= 10 , trova un punto $ in modo tale che, detta " la sua
Su una semicirconferenza di diametro + $
= 12 .
proiezione su , sia "
Problema 215.210
Soluzione
= A
Poniamo "
e
= n
$
con i limiti geometrici: 0 < A < 10
e
0 < n < 10
Per il I° T. di Euclide applicato al triangolo rettangolo $ si ha:
r
r
A + n = 12
n = 10 ∙ 10 − A
n = 12 − A
p
A − 14A + 44 = 0
r
n = 12 − A
p
12 − A = 100 − 10A
n = 12 − A
p
r
144 + A − 24A − 100 + 10A = 0
Da cui si ricava:
A,
\
\ − 428 ± 34 8 − [ 7 ± √49 − 44
2
=
=
= 7 ± √5
[
1
Le soluzioni sono entrambe accettabili perché entrambe positive e minori di 10.
Matematica
www.mimmocorrado.it
21