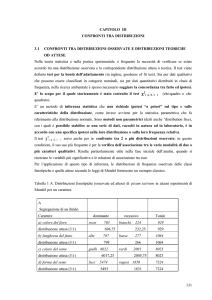
1) Su un collettivo di n = 11 coppie residenti a Roma si sono rilevati i seguenti dati, circa il numero di figli minorenni
(X) e la spesa sostenuta durante il mese di dicembre per spettacoli, in euro (Y).
X
Y
2
54
1
19
1
64
4
14
2
95
0
61
2
48
1
80
3
51
1
40
0
36
A) Con riferimento al carattere X
determinare le frequenze e la moda
rappresentare la distribuzione con un diagramma a barre
B) Con riferimento al carattere Y, calcolare la media aritmetica, la mediana e la varianza
C) Sempre con riferimento al carattere Y
suddividere i dati in 3 classi di ampiezza 30 , in un campo di variabilità da 10 a 100 e costruire la distribuzione delle
frequenze e rappresentare la suddetta distribuzione mediante istogramma
D) Mantenendo sempre il raggruppamento in classi, scrivere una tabella a doppia entrata, secondo i due caratteri
numero di figli / fascia di spesa e fornire un’opportuna rappresentazione grafica.
SOLUZIONE
2)
a) Nelle prove di allenamento per una gara di salto in alto , l'atleta A effettua le seguenti prestazioni
( in metri)
1,88
1,95
2,01
1,98
1,95
1,98
2,01
1,98
1,96
Calcola le frequenze e disegna l'ogiva delle frequenze cumulate
Determina la media aritmetica e la mediana della distribuzione
Verifica che eliminando il risultato nettamente più basso risulta alterata la media ma non la mediana
b) Nel corso delle gare, il suddetto atleta effettua le seguenti prestazioni
SALTO IN ALTO (in metri)
1,97
100 METRI ( in secondi)
10,10
LANCIO DEL PESO(in metri)
17,60
Sapendo che, nelle gare considerate, media e deviazione standard delle distribuzioni (dei risultati di tutti gli atleti)
sono risultate rispettivamente
media
deviazione standard
salto in alto
1,99
0,19
100 metri
10,30
1,21
lancio del peso
17,80
2,25
determina in quale
sport l'atleta A ha fornito la peggiore prestazione.
c) Confronta la prestazione nel salto in alto con la distribuzione delle prestazioni dell'atleta A durante gli allenamenti e
stabilisci la sua posizione rispetto ai quartili.
SOLUZIONE
3) Sono qui di seguito riportati gli esiti degli Esami di Stato delle classi VA e Vb di un Liceo romano, abbinate nella
medesima Commissione ( i voti sono espressi in centesimi)
VA
ANGELINI Massimo
BELLINI
Giovanni
CARELLA Luca
CINI
Alessia
DE NIGRIS Marco
DI MAIO
Fabio
FERRARA Enrico
FUCCI
Guglielmo
LELLI
Marianna
LORENA Diego
MARCELLINI Giulia
NISTRI
Alessandra
ORTISEI
Giovanna
PEZZI
Francesca
RATTI
Paolo
TROTTA Simone
VECCHI
Luciana
VILLA
Angelo
ZANETTI
Aldo
65
75
96
80
70
72
87
66
83
72
100
82
90
70
60
100
78
60
70
VB
BIANCHI Claudia
BRAVI
Riccardo
CONTI Marco
CORSO Antonio
EVANGELISTA Lucio
FANI
Daniela
GELLI Alessandro
GHINI Fabio
LOMBARDI Chiara
MARTELLI Francesco
MOSCA
Daniele
MUCCI
Roberta
NONIS
Paola
ROTA
Fabio
SCHIAVI Andrea
TIRELLI Stefano
ZOLLO Serena
80
75
70
90
85
95
84
100
96
86
78
72
82
74
62
90
84
a) Per ciascuna distribuzione determina la Media, la Mediana e lo Scarto quadratico medio Quale delle due classi
presenta un rendimento più omogeneo?
b) Tenendo conto dell’andamento della classe, è migliore la prestazione dell’allievo Bellini della VA o dello studente
Bravi della VB? E quella di Marcellini e di Trotta rispetto della VA all’allievo Ghini della VB?
c) Raggruppare i voti in classi 60- 65
65-70
70- 75
75-80 80-85 85-90 90-95 95-100 e
rappresentare ciascuna distribuzione mediante istogrammi
d) Mantenendo sempre il raggruppamento in classi, scrivere una tabella a doppia entrata, secondo i due caratteri
classi / votazioni e completarla con le distribuzioni marginali
Costruire una tabella analoga con le frequenze relative in formato percentuale
e) Verificare se c’è differenza significativa fra le due distribuzioni
SOLUZIONE