Esercizio n. 1
aria
acqua
Φ
0
(amb)
1
3
2
risposte ai quesiti
Una miscela di gas scorre alla velocità
in un condotto di
diametro
. Sapendo che la miscela si trova a pressione
1)
e temperatura ambiente, e che la sua composizione in volume è:
He
70% (vol.)
N2
20% (vol.)
CO2
10% (vol.)
si determinino:
2)
1) la portata massica ̇ (g/s);
2) il flusso termico (kW) necessario per portare detta
miscela alla temperatura
.
La temperatura viene quindi regolata al valore
mediante
miscelazione con una portata di aria (secca) a temperatura
ambiente. Calcolare:
3) la portata massica ̇ (g/s) di aria necessaria;
4) la composizione in volume della miscela risultante.
Infine, nell’ipote i di umidificare il fluido tramite iniezione di una
portata di acqua ̇
(disponibile in fase liquida a
pressione e temperatura ambiente), determinare:
5) la temperatura finale della miscela nel punto 3,
;
6) l’u idità relativa
(%).
Si proceda sotto le seguenti assunzioni ed approssimazioni:
a. pressione ambiente
at ;
b. temperatura ambiente
;
c. perdite di carico trascurabili;
d. composizione in volume dell’aria a biente: N2 79%, O2 21%;
e. calore specifico a pressione costante rispondente alla teoria
cinetica dei gas ideali (e costante con la temperatura):
per gas monoatomici
per gas biatomici
per gas triatomici
f. calore pecifico a pre ione co tante del vapor d’acqua
costante con la temperatura e pari a
;
g. entalpia sensibile dei gas perfetti nulla alla temperatura
(
);
ambiente: ( )
h. calore latente di vaporizzazione dell’acqua co tante e pari a
;
i. comportamento del vapor d’acqua surriscaldato
approssimabile a quello di gas perfetto;
j. comportamento dell’acqua “sottoraffreddata” approssimabile a
quello di liquido perfetto.
̇
=
g/s
=
kW
=
g/s
=
°C
=
%
3)
̇
4)
5)
6)
Esercizio n. 2
Una miscela di gas è contenuta in un serbatoio di volume
alla pressione
e temperatura
.
La composizione in volume della miscela è la seguente:
CO
20% (vol.)
N2
30% (vol.)
CO2
50% (vol.)
Si determinino innanzitutto:
1) la massa di miscela contenuta nel serbatoio
( );
2) la composizione in massa della miscela.
risposte ai quesiti
1)
=
2)
kg
composizione massica
Si consideri quindi un riscaldamento del serbatoio tramite un
flusso termico
applicato per un tempo
. Si
calcolino:
3) le condizioni di temperatura ( ), pressione ( ) e
densità (
) alle quali si trova la miscela al termine
del suddetto processo di riscaldamento.
Nell’ipote i di introdurre nel serbatoio una quantità di aria (secca),
disponibile alla temperatura
, tale da portare la
temperatura della miscela risultante (miscela originaria + aria) al
valore
, determinare inoltre:
4) la massa presente nel serbatoio al termine di detto
miscelamento,
( );
5) la composizione in volume della miscela risultante;
6) la pressione ( ) e la densità (
) della miscela
risultante.
3)
Si chiede infine di:
7) rappresentare sul piano T-s la trasformazione (1-2-3)
subita dal componente CO presente nella miscela.
4)
Si proceda sotto le seguenti assunzioni ed approssimazioni:
k. composizione in massa dell’aria secca: N2 77%, O2 23%;
l. calore specifico a pressione costante rispondente alla teoria
cinetica dei gas ideali (e costante con la temperatura):
per gas monoatomici
per gas biatomici
per gas triatomici
5)
=
°C
=
bar
=
kg/m
=
kg
3
composizione in volume
6)
=
bar
=
kg/m
7) sul foglio
3
Esercizio n. 3
c2
c1
sez. 1
sez. 2
Si consideri il condotto in figura percorso da una miscela di gas
caratterizzata dalla seguente composizione:
He
45% vol.
O2
35% vol.
Ar
20% vol.
e dalle seguenti condizioni di funzionamento nominale:
portata gas
̇
=
2,0
temperatura (di ristagno)
= 250
pressione (di ristagno)
=
3,0
velocità del fluido all’in re o
=
20
pressione allo scarico del condotto
=
2,5
risposte ai quesiti
1)
kg/s
°C
bar
m/s
bar
(% massa)
2)
=
m
3)
=
m
Nell’ipote i che il condotto così dimensionato si trovi ad operare con le
te e condizioni ter odina iche del fluido all’in re o
, ) ma con
una pressione allo scarico pari a
bar, calcolare, supponendo
invariato il rendimento isoentropico:
6) la portata di gas che il condotto è in grado di elaborare ̇ (kg/s).
4)
=
°C
Si determini inoltre:
7) la pressione allo scarico che determina il raggiungimento delle
condizioni soniche in uscita
(bar).
5)
=
m/s
Si chiede infine di:
8) rappresentare su un opportuno diagramma termodinamico le
trasformazioni del fluido nelle diverse condizioni assegnate,
evidenziando le energie cinetiche in gioco e rispettando
orientativamente le scale delle grandezze rappresentate.
6)
Sulla base delle condizioni sopra assegnate, si calcolino:
1) la composizione in massa del fluido;
2) il dia etro del condotto all’in re o del fluido
(m);
3) il diametro del condotto allo scarico
(m);
4) la temperatura del fluido allo scarico
(°C);
5) la velocità del fluido allo scarico (m/s).
Si proceda sotto le seguenti assunzioni ed approssimazioni:
a. calore specifico a pressione costante rispondente alla teoria
cinetica dei gas ideali (e costante con la temperatura):
per gas monoatomici
per gas biatomici
b. efflusso ideale (rendimento isoentropico unitario) in tutte le
condizioni di funzionamento assegnate.
̇
7)
8)
=
=
sul foglio
kg/s
bar
Esercizio n. 4
𝑚̇
Φ
Φ
2
𝑚̇
1
3
5
4
𝑚̇ 𝑤
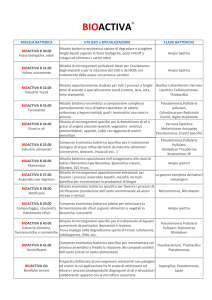
Si consideri un flusso di aria umida (sezione 1 in figura) caratterizzato
dalle seguenti condizioni:
portata di aria secca
̇
=
1 kg/s
temperatura
= 40 °C
pressione
= 1,1 bar
umidità relativa
= 80 %
Tale flusso sia miscelato con un secondo flusso (sezione 2 in figura)
per il quale valgano le seguenti condizioni:
portata di aria secca
̇
= 0,5 kg/s
temperatura
= 30 °C
umidità relativa
= 80 %
Si determinino innanzitutto:
1) la portata di aria umida nella sezione 3 ̇
(kg/s);
2) la temperatura
del flusso risultante dalla miscelazione (°C);
3) l’u idità relativa
di detto flusso (%).
La portata di aria umida ottenuta è quindi sottoposta ad un
raffreddamento con condensazione (trasformazione 3-4) e ad un
successivo riscaldamento (trasformazione 4-5), al fine di ottenere nella
sezione finale le seguenti condizioni:
temperatura
= 25 °C
umidità relativa
= 50 %
Si calcolino:
4) la temperatura a valle della prima trasformazione (°C);
5) la portata d’acqua conden ata ̇ (g/s);
6) il flusso termico complessivamente richiesto nel processo di
raffreddamento con condensazione
(kW);
7) il flusso termico richiesto per la sola condensazione
(kW);
8) il flusso termico richiesto per il riscaldamento finale
(kW).
Si proceda sotto le seguenti assunzioni ed approssimazioni:
a. perdite di carico trascurabili;
b. calore pecifico a pre ione co tante dell’aria ecca co tante
con la temperatura e pari a
;
c. calore pecifico a pre ione co tante del vapor d’acqua
costante con la temperatura e pari a
;
d. entalpia sensibile dell’aria ecca nulla a
e dunque
valutabile con la relazione: ( )
( temperatura in );
e. calore latente di vaporizzazione dell’acqua co tante e pari a
;
f. comportamento del vapor d’acqua surriscaldato
approssimabile a quello di gas perfetto;
g. comportamento dell’acqua “sottoraffreddata” approssimabile a
quello di liquido perfetto.
risposte ai quesiti
̇
1)
=
kg/s
2)
=
°C
3)
=
%
4)
=
°C
=
g/s
6)
=
kW
7)
=
kW
8)
=
kW
5)
̇