LE FRAZIONI
Sappiamo che i numeri naturali non consentono di eseguire le sottrazioni nei casi in cui il
sottraendo e` maggiore del minuendo. Per tale motivo e` stato necessario introdurre i numeri interi
relativi. Ma anche i numeri interi relativi non sono sufficienti a risolvere tutti i problemi.
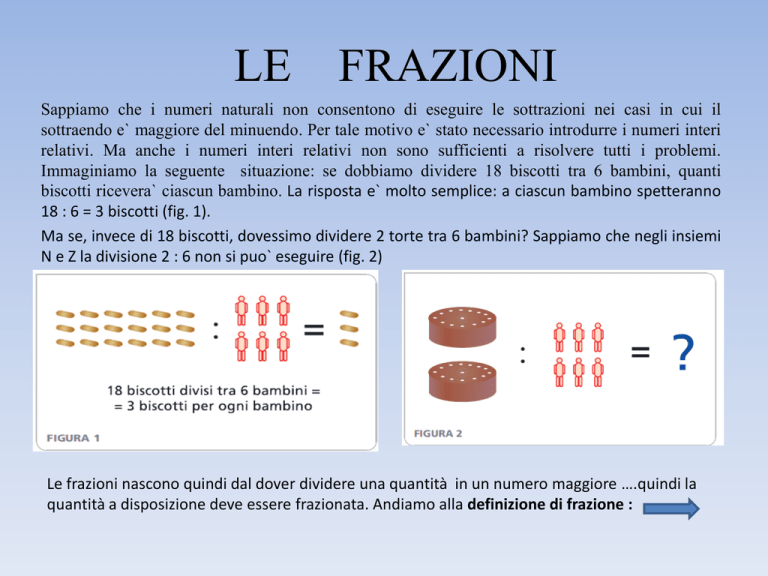
Immaginiamo la seguente situazione: se dobbiamo dividere 18 biscotti tra 6 bambini, quanti
biscotti ricevera` ciascun bambino. La risposta e` molto semplice: a ciascun bambino spetteranno
18 : 6 = 3 biscotti (fig. 1).
Ma se, invece di 18 biscotti, dovessimo dividere 2 torte tra 6 bambini? Sappiamo che negli insiemi
N e Z la divisione 2 : 6 non si puo` eseguire (fig. 2)
Le frazioni nascono quindi dal dover dividere una quantità in un numero maggiore ….quindi la
quantità a disposizione deve essere frazionata. Andiamo alla definizione di frazione :
Definizione di Frazione: è una coppia ordinata di numeri naturali, con il
secondo diverso da zero. E’ del tipo
, dove il primo numero m è il
m
n
numeratore della frazione ed il secondo n è il denominatore.
Esempio:
Linea di frazione
2
5
Numeratore
Denominatore
Il numeratore indica le parti prese, il denominatore il numero
di parti in cui è stato diviso l’intero!
La frazione
2
5
si legge “ due quinti”
Sta ad indicare che l’intero viene diviso in cinque parti (pari al numero che si ha
al denominatore e se ne prendono due di queste parti (pari al numero che si ha al
numeratore.
E si rappresenta cosi:
La frazione come operatore:
la frazione
m
n
puo è un operatore che ci permette di dividere l’intero in parti
uguali e di considerarne alcune di esse.
Quindi per operara con una frazione m si deve DIVIDERE l’intero in n parti
n
uguali e prendere m parti ottenute dalla divisione.
TIPI DI FRAZIONI
Le frazioni possono essere: PROPRIE, IMPROPRIE, APPARENTI, COMPLEMENTARI
TIPI DI FRAZIONI
frazioni equivalenti
hanno lo stesso valore
Le frazioni
1
2
e
2
4
sono
equivalenti perché hanno
lo stesso valore, in quanto,
corrispondono alla stessa
parte di unità come si vede
dalla loro rappresentazione
Se moltiplichiamo per uno stesso numero sia
il numeratore che il denominatore otteniamo
infinite frazioni equivalenti
3 = 6 = 9 = 12 = 15 = 18
5
10
15
20
25
30
…
viceversa, si possono dividere per uno stesso
numero il numeratore e il denominatore
18 = 9 = 6 =
30
15
10
3
5
3/5 è la frazione
ridotta ai
minimi termini
Per semplificare una frazione basta dividere per uno stesso
numero il numeratore e il denominatore. Si ottiene una frazione
equivalente con termini più piccoli.
Es. 20 = 10 = 2
30 15 3
Per semplificare la frazione 20/30 Abbiamo diviso x2 e poi x5 .
Potevamo dividere direttamente x10 (M.C.D.) ottenendo 2/3,
frazione ridotta ai minimi termini.
Per semplificare una frazione in un solo passaggio basta dividere
numeratore e denominatore per il loro MASSIMO COMUNE DIVISORE.
ESERCIZI:
1) Rappresenta graficamente le seguenti frazioni:
1
2
3
6
3
4
4
7
Ci sono frazioni equivalenti?
2) Indica per ogni frazione se è propria, impropria, apparente:
3
2
7
8
12
6
5
4
3
4
30
5
30
18
3) Semplifica le seguenti funzioni:
12
20
150
120
4) Semplifica le seguenti frazioni calcolando il massimo comune divisore:
150
120
42
30
90
18
150
300
5) Scrivi le frazioni complementari delle seguenti frazioni:
3
5
5
6
4
7












