Schema ripasso integrali indefiniti e definiti

a.s.2009/10
ISIS Facchinetti di Castellanza
classe 5 CH
INTEGRALI
Traccia per il ripasso delle questioni fondamentali e la risistemazione degli appunti
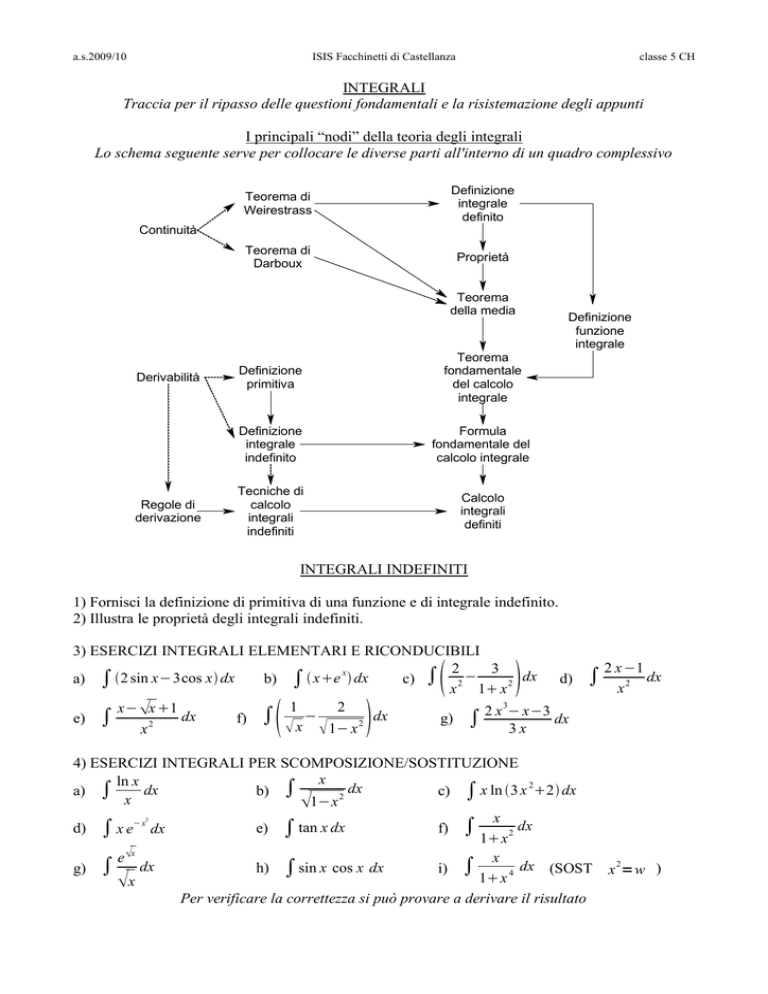
I principali “nodi” della teoria degli integrali
Lo schema seguente serve per collocare le diverse parti all'interno di un quadro complessivo
Teorema di
Weirestrass
Definizione
integrale
definito
Teorema di
Darboux
Proprietà
Continuità
Teorema
della media
Derivabilità
Regole di
derivazione
Definizione
primitiva
Teorema
fondamentale
del calcolo
integrale
Definizione
integrale
indefinito
Formula
fondamentale del
calcolo integrale
Tecniche di
calcolo
integrali
indefiniti
Calcolo
integrali
definiti
Definizione
funzione
integrale
INTEGRALI INDEFINITI
1) Fornisci la definizione di primitiva di una funzione e di integrale indefinito.
2) Illustra le proprietà degli integrali indefiniti.
3) ESERCIZI INTEGRALI ELEMENTARI E RICONDUCIBILI
2
3
x
dx d)
a) ∫ 2 sin x−3cos x dx
b) ∫  xe  dx
c) ∫ 2 −
x 1 x 2
1
2
x− x 1
2 x 3− x−3
−
dx
dx
e) ∫
f) ∫
g) ∫
dx
2
2
 x  1− x
3x
x




∫
4) ESERCIZI INTEGRALI PER SCOMPOSIZIONE/SOSTITUZIONE
x
ln x
2
dx
dx
a) ∫
b) ∫
c) ∫ x ln 3 x 2 dx
2
x
1−x
x
dx
d) ∫ x e− x dx
e) ∫ tan x dx
f) ∫
1x 2
e x
x
dx (SOST
dx
h) ∫ sin x cos x dx
g) ∫
i) ∫
1x 4
x
Per verificare la correttezza si può provare a derivare il risultato
2 x −1
dx
x2
2
2
x =w )
a.s.2009/10
ISIS Facchinetti di Castellanza
classe 5 CH
5) INTEGRALI PER PARTI
Ricava, partendo dalla formula di derivazione del prodotto di due funzioni, la formula di
integrazione per parti. Applicala quindi alla risoluzione dei seguenti integrali
−x
2
a) ∫ ln x dx
b) ∫ x e dx
c) ∫ x ln x dx
d) ∫ x sin x dx
ln x
−2 x
2 −x
e) ∫ 2 dx
f) ∫ artg x dx
g) ∫ x e dx
h) ∫ x e dx
x
6) ALTRI INTEGRALI (questione da approfondire in classe)
3 x−2
x−1
2 x−5
dx
dx
dx
a) ∫
b) ∫
c) ∫ 2
x1
3 x1
x 1
d)
∫
3 x2
dx
 1−x 2
INTEGRALI DEFINITI (le dimostrazioni sono consigliate ma non obbligatorie)
1) Fornisci la definizione di integrale definito
2) Illustra il significato geometrico dell'integrale definito
3) Illustra le proprietà dell'integrale definito
4) Enuncia il teorema della media integrale e illustrane il significato grafico
5) Enuncia e dimostra il teorema della media integrale
6) Determina e rappresenta graficamente
a) il valore medio della funzione f  x =1−x 2 nell'intervallo [-1,1]
b) i valori di x in cui la funzione assume tale valore medio.
c) ripeti l'esercizio con f  x = x 22 nell'intervallo [-2,0]
7) Fornisci la definizione di funzione integrale e mostrane il significato attraverso un esempio
grafico
8) Enuncia il teorema fondamentale del calcolo integrale; ricava quindi l'espressione analitica della
x
t
funzione F  x =∫ −1 dt
2 2
9) Enuncia e dimostra il teorema fondamentale del calcolo integrale
10) Enuncia la formula fondamentale del calcolo integrale e mostrane un esempio di applicazione
11) Enuncia e dimostra la formula fondamentale del calcolo integrale.
 
12) ESERCIZI INTEGRALI DEFINITI SEMPLICI
−1
a)
x−1
dx
∫
∫  x −1
2
dx
b)
−2
c)
x
1
3
5 / 6
4
2
∫
sen x dx
d)
/ 3
2
dx
∫ 1x
2
1
13) ESERCIZI INTEGRALI DEFINITI PER SOSTITUZIONE
 /3
e
ln 2 x
dx
a) ∫
x
1
b)
0
2
3
d)
∫ x  1 x
2
3
dx
∫
1/ 3
1
x 1x 
c)
 /3
dx
h)
2
∫
0
sin x
2
x
∫  x 22
2
1
e
e−1/ x
e) ∫ 3 dx
x
1
0
g)
2
∫ sin x cos2 x dx
f)
∫
1/ e
1
dx
i)
cos x
∫
 2 /2
ln x
dx
dx
x
x
dx (SOST.
 1− x 4

2
l) Sapendo che vale l'identità cos 2 x=1 – 2 sin x determina
∫ sin 2 x dx
0
14) INTEGRALI DEFINITI PER PARTI
2
e
a)
∫ x ln x dx
e
 /4
4
b)
∫xe
0
x/ 2
dx
c)
∫ x cos  2 x dx
0
x 2=w )