Condensatore elettrico

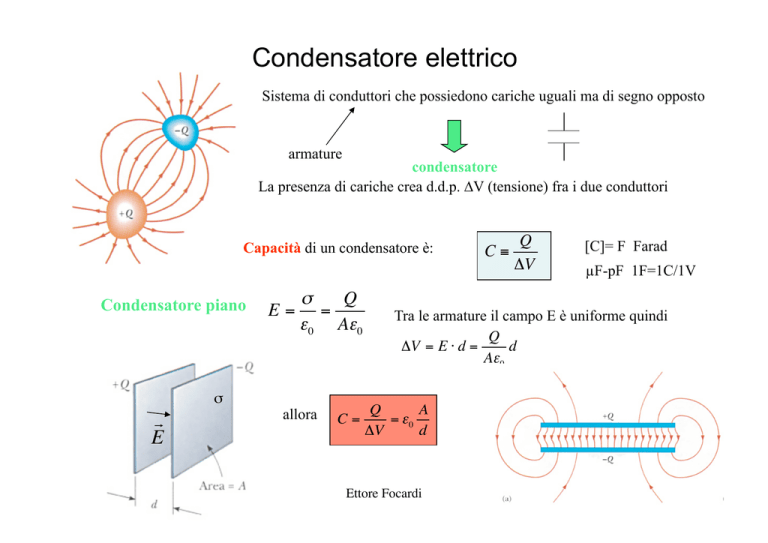
Condensatore elettrico
Sistema di conduttori che possiedono cariche uguali ma di segno opposto
armature
condensatore
La presenza di cariche crea d.d.p. ∆V (tensione) fra i due conduttori
Capacità di un condensatore è:
Condensatore piano

E
€ σ
E=
allora
€
€
σ
Q
=
ε0 Aε0
C≡
Q
ΔV
[C]= F Farad
µF-pF 1F=1C/1V
Tra le armature il campo E è uniforme quindi
€
Q
ΔV = E ⋅ d =
d
Aε0
Q
A
C
=
=
ε
0
€ ΔV
d
Ettore Focardi
1
Condensatori con dielettrici
Dielettrico materiale non conduttore, come gomma, vetro, carta….
Se introdotto tra le armature C aumenta
di un fattore εr (costante dielettrica)
C= εr C0
Condensatore piano
ε0 A
d
C aumenta diminuendo d però fino
a quando non si innesca scarica elettrica
attraverso il dielettrico
€
Rigidità dielettrica (max ∆V per un certo d)
∆V<∆V0
Materiale
Aria
Carta
Vetro pirex5.6
Ettore Focardi
C = εr
εr
1.00059
3.7
14x106
rigidità
V/m
3x106
16x106
2
Tipi di condensatori
Alte tensioni
Elettrolitico
per grandi accumuli carica
imbevuta di paraffina
Per piccoli condensatori si usano materiali ceramici
Ettore Focardi
Sottile strato di dielettrico
su metallo, grande capacità
Attenzione alla polarità
3
esempi
1) 
Condensatore a carta.
Un condensatore piano ha le armature di dimensioni a=2 cm, b=3 cm,
separate da una distanza d=1 mm.
Quanto vale la capacita’?
Qual e’ la massima tensione applicabile?
Per la carta e’ εr=3.7, quindi:
2
ε0 S
6 10 -4 m 2
-12 C
C = εr
= 3.7(8.85 10
)(
) = 20 pF
2
-3
d
Nm 1 10 m
Rigidita’ carta: 16 106 V/m, quindi:
€
ΔVmax = E max d = (16 10 6 V /m)(1 10 -3 m) = 16 10 3 V
€
Ettore Focardi
4
esempi
2) Energia immagazzinata con e senza dielettrico.
Sul condensatore C0 si deposita la carica Q0 con la batteria ∆V0.
Si stacca poi la batteria e si inserisce una lastra di cost. εr.
L’energia immagazzinata in C0 a vuoto e’
1 Q02
U0 =
2 C0
All’inserimento del dielettrico e senza batteria,
Q0 resta la stessa e quindi l’energia sara’:
€
2
2
U=
€
Q0
Q0
U
=
= 0 < U0
2C 2εrC0 εr
La diminuzione di energia si spiega osservando che
il dielettrico inserito, e’ attratto dalle piastre.
La forza ha origine dalla non uniformita’ del campo
ai bordi;
la componente orizzontale agisce sulle cariche indotte
sulla superficie del dielettrico, dando luogo
alla forza diretta verso l’interno del condensatore.
Ettore Focardi
5
conduttori-dielettrici
Riferimento ad interpretazione microscopica.
Conduttori: metalli caratterizzati da struttura cristallina con atomi ai vertici di reticolo
poliedrico.
La disposizione degli atomi nel reticolo e quindi l’andamento spaziale del
potenziale della forza che attrae e- ai nuclei e’ tale che 1-2 e- delle orbite esterne
siano liberi ( energia di legame ≤ energia di agitazione termia a Tamb).
Se si applica E le cariche si muovono.
Dielettrici: atomi e molecole con e- ben legati ai nuclei.
Per forti interventi localizzati (strofinio), si possono spostare cariche.
In genere sono complessivamente neutri.
In presenza di campo esterno si puo’ avere momento di dipolo ≠0,
si dice allora che il dielettrico e’ polarizzato.
Ettore Focardi
6
Dipolo in campo E
Vediamo l’effetto di un campo elettrico su di un dipolo elettrico.
momento di dipolo elettrico p=q2a
Le forze agenti sulle cariche F=qE sono opposte → R(e)=0;
esse esercitano una coppia che tende a ruotare il dipolo per
allinearsi al campo.
Il momento della forza sulla carica positiva rispetto ad un asse
passante per O e’ F a senθ con a senθ=b braccio di F rispetto ad O.
Tale momento tende a produrre una rotazione oraria.
Il momento di F su -q rispetto ad O e’ ancora F a senθ, quindi:
M = 2Fasenθ = 2qEasenθ = pEsenθ
In forma
€ vettoriale e’:
  
M = p∧ E
Ettore Focardi
7
Energia potenziale di un dipolo
Vogliamo calcolare l’energia potenziale di un dipolo elettrico in un campo elettrico esterno in funzione
della sua orientazione rispetto al campo.
Se il dipolo e’ allineato con il campo elettrico un agente esterno deve compiere lavoro per ruotare il dipolo fino
ad un dato angolo. Il lavoro eseguito e’ immagazzinato come energia potenziale del sistema dipolo-campo.
F
Il lavoro dW richiesto ad una forza F per ruotare il dipolo di dθ e’:
ds
φ
P si sposta di ds = r dθ
dθ
O
r
 
dW = F ⋅ ds = Fsenφrdθ = qEsenφr dθ = Mdθ
P
Con M momento di F rispetto ad O, che dalla precedente da’ M=pE senθ
D’altra parte il lavoro viene trasformato in energia potenziale U e per una rotazione finita
aa θI a θf, la variazione ∆U sara’:
€
ΔU = U f − U i =
θf
θf
∫ Mdθ = ∫ pEsenθdθ = pE(−cosθ )
θi
θi
θf
θi
= pE(cosθ i − cos θ f )
Il termine in cui compare θi e’ una costante dipendente dalla posizione iniziale del dipolo.
 
Conviene scegliere θI=900 e quindi:
U = − pE cos θ = − p ⋅ E
€
Da un confronto con l’energia potenziale gravitazionale U=mgh, si nota come nei due casi si modifichi il
sistema, una volta in dipendenza dall’altezza dell’oggetto e nell’altra con la rotazione del corpo.
€ il corpo tende a tornare nella posizione iniziale, a terra o allineato ad E.
In entrambi i casi, se lasciato libero,
Ettore Focardi
8
Molecole polarizzate
Le molecole sono dette polarizzate quando il baricentro delle cariche positive e’ diverso da quello delle
cariche negative.
Per la molecola dell’acqua questa condizione e’ sempre verificata, e’
quindi detta molecola polare.
Si ha cosi’ un momento di dipolo p ≠ 0
A livello macroscopico l’effetto di p non si manifesta poiche’ le
molecole sono orientate a caso <p>=0.
Se c’e’ un campo elettrico i dipoli si allineano al campo.
Es. Forno a microonde:
il forno produce un campo elettrico variabile rapidamente che mette in oscillazione le molecole di acqua ;
queste assorbono energia dal campo e per gli urti provocati da tale moto tale energia si converte in
energia interna che aumenta la temperatura del corpo.
Una molecola simmetrica non ha polarizzazione permanente, ma
un momento di dipolo puo’ essere indotto da una campo esterno.
Il campo elettrico sposta la carica - e induce una
polarizzazione per deformazione
Questo e’ l’effetto dominante nella maggior parte dei materiali
usati come dielettrici nei condensatori.
Ettore Focardi
9
Modello dielettrici
Nel caso di un condensatore piano riempito di dielettrico di costante εr e’:
∆V= ∆V0/εr e poiche’ ∆V= E d e’ E=E0/εr
Se il materiale dielettrico tra le armature e’ costituito da molecole polari,
si ha una orientazione casuale in assenza di campo elettrico, che diventa
allineamento con la presenza del campo E0. Il grado di allineamento dipende
dalla temperatura e dall’intensita’ del campo.
Se le molecole del dielettrico sono non polari il campo elettrico esterno delle
armature produce un momento elettrico di dipolo e una polarizzazione per
deformazione, con i momenti di dipolo indotti che tendono ad allinearsi con
campo elettrico esterno. Possiamo polarizzare qualunque dielettrico.
E=E0-Eind nel dielettrico
Eind
E0=σ/ε0 Eind= σind / ε0
Ma E=E0 / εr
σ
σ σ
ε −1
= − ind → σ ind = r σ
ε0εr ε0 ε0
εr
dato che εr>1 e’ σind < σ
€
Ettore Focardi
10
esempi
1) 
Effetto di una lastra metallica.
Un condensatore piano ha le armature di area A a distanza d.
Una lastra di metallo scarica di spessore a, e’ inserita al centro. Calcolare C.
Sulla lastra viene indotta una carica opposta su ciascuna faccia
con stessa densita’ σ come sulle armature;
la carica totale sulla lastra e’ dunque nulla e E=0.
Quindi il condensatore equivale a due condensatori in serie con distanza tra le
armature (d-a)/2.
1 1
1
= +
=
C C1 C2
1
1
+
ε0 A
ε0 A
(d − a) /2 (d − a) /2
ε0 A
C=
d−a
Ettore Focardi
€
€
11
esempi
2) Condensatore parzialmente riempito.
Un condensatore piano con armature distanti d ha capacita’ C0 in assenza di dielettrico.
Si inserisce tra le armature una lastra dielettrica di costante εr e spessore d/3. C?
Nell’esempio precedente, potevamo considerare il
condensatore come composto da due condensatori in
serie indipendentemente dalla posizione della lastra.
Inoltre quando lo spessore della lastra
tende a 0, C tende a quella in assenza di lastra.
Si suppone allora di inserire una lastra metallica sottile
sotto la superficie inferiore del dielettrico.
C1 =
1
d /3 2d /3
d 1+ 2εr
=
+
=
(
)
C εrε0 A ε0 A 3ε0 A εr
€
C=
Ettore Focardi
€
€
εrε0 A
d /3
C2 =
ε0 A
2d /3
3εr ε0 A
3εr
=
C0
2εr + 1 d
2εr + 1
12