itis savignano s/r - Digilander

LABORATORIO
NUCCI ANDREA
DI SISTEMI
3ª-B
E AUTOMAZIONE
DATA
INDUSTRIALE
07/04/2001
ITIS SAVIGNANO S/R
TITOLO: Rilievo dello sfasamento tra tensione (V) e intensità (I)
OGGETTO: Verifica dello sfasamento della corrente in un circuito tramite oscilloscopio
SCOPO: Determinare lo sfasamento tra tensione e intensità di corrente di un circuito attraversato
da corrente alternata, a seconda che il circuito sia :
1. PURAMENTE OHMICO
2. PURAMENTE CAPACITIVO
3. PURAMENTE INDUTTIVO
DESCRIZIONE DEI MATERIALI E DEGLI STRUMENTI:
1. Generatore di frequenza (TOPWARD (mod.8112 DIGITAL FUNCTION GENERETION)
2. Oscilloscopio una Ohm (mod G 4020 20MHz)
3. 2 Resistenze
4. Bobina (mod DX54977 9,5mH)
5. Vari cavi di collegamento e pinze di collegamento
6. Basette di collegamento
7. Condensatore (1F)
RICHIAMI TEORICI:
Oscilloscopio: E’ lo strumento che serve per l’osservazione diretta dell’andamento di fenomeni
variabili nel tempo, fenomeni periodici di qualsiasi natura, anche di frequenza molto elevata,
purché le grandezze da osservare possano essere convertite in tensioni elettriche mediante opportuni
trasduttori, è lo strumento molto diffuso nel campo delle misure elettroniche. L’uso di questo
apparecchio è molto complesso, perciò è una vasta gamma di pulsanti e comandi. Con
l'oscilloscopio è possibile effettuare misure di tensione, di corrente, di frequenza e di intervalli di
tempo; rappresentare la curva di risposta in frequenza.
ITI SAVIGNANO RELAZIONE N.4Rilievo
dello sfasamento tra tensione (V) e intensità (I) Pag.1
ITI SAVIGNANO RELAZIONE N.4Rilievo
dello sfasamento tra tensione (V) e intensità (I) Pag.2
Corrente alternata: (AC) caratterizzata dal fatto di alternare periodicamente il suo verso di
scorrimento nei conduttori (e dunque nei circuiti) , nel tempo (t) con legge periodica in modo tale
che il valore medio dell’intensità sia nullo. L’intensità I delle correnti alternate più comuni varia nel
tempo (t) con legge sinusoidale I=I0*sen (2f*t-); V0 è il massimo valore della differenza di
potenziale V e  angolo di fase, tiene conto del fatto che l’intensità di corrente e la tensione che la
produce non sono generalmente in fase, cioè non raggiungono i valori massimi e minimi nello
stesso istante.
Reattanza: Si dice reattanza l’ostacolo che l’induttanza L oppone al passaggio della corrente
alternata. La reattanza viene indicata con la lettera X, X L é la reattanza induttiva ovvero l'ostacolo
che l’induttanza L oppone al passaggio della corrente, XC l'ostacolo che il condensatore C oppone
al passaggio della corrente.
Induttanza: Parametro che caratterizza la risposta di un circuito elettrico alle variazioni di corrente
nel tempo unitario. In seguito alla variazione di corrente, ai capi del circuito si genera una
differenza di potenziale (che a sua volta produce una forza elettromotrice) pari a V = LdI/dt: la
costante di proporzionalità fra V e la variazione di corrente dI/dt è appunto l’induttanza del circuito,
o coefficiente di autoinduzione. La sua unità di misura nel Sistema internazionale è l’henry (H),
equivalente a ×s.
CIRCUITO PURAMENTE RESISTIVO
Un circuito si dice puramente resistivo quando compaiono solo resistenze. Lo schema elettrico è il
seguente:
R1
Puramente ohmico o resistivo
(CH1)
canale 1
(CH2)
canale 2
G
~
R2
ITI SAVIGNANO RELAZIONE N.4Rilievo
Resistenza
ausiliaria
V
IM
dello sfasamento tra tensione (V) e intensità (I) Pag.3
Puramente resistivo
VM
IM
t

2
Nel circuito puramente resistivo la corrente è in fase con la tensione. La legge di Ohm diventa:
V=RI
Dove V e I sono vettori; mentre R la consideriamo costante. Usando i vettori rotanti otteniamo che
il vettore corrente è parallelo al vettore tensione, in quanto tensione e corrente sono in fase.
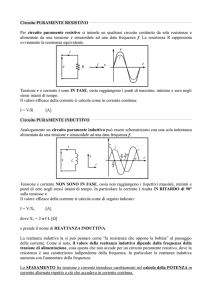
CIRCUITO PURAMENTE INDUTTIVO
Un circuito si dice puramente induttivo quando compaiono solo delle induttanze. Lo schema
elettrico è il seguente:
Puramente induttivo
Induttanza
(CH1)
canale 1
(CH2)
canale 2
G
~
R2
V
Resistenza
ausiliaria
  90o
IM
Nella induttanza L, essendo sottoposta a corrente alternata vi si genera una forza elettromotrice
indotta e, secondo la legge di Farady, Neumann, Lenz, tale forza elettromotrice è uguale e opposta
alla tensione che l'ha generata, cioè v = - e.
ITI SAVIGNANO RELAZIONE N.4Rilievo
dello sfasamento tra tensione (V) e intensità (I) Pag.4
Puramente induttivo
VM
IM
t
Si dice reattanza induttiva l'ostacolo che la induttanza L oppone al passaggio della corrente
alternata. La reattanza induttiva si indica con la lettera XL, si misura in  , si calcola con la
seguente formula:
XL =  L
Tale formula ci dice che la reattanza della bobina avente induttanza L è pari al prodotto della
pulsazione  per l'induttanza L della bobina. Dove  = 2  f.
Tra tensione e corrente nel condensatore esiste uno sfasamento di 90° , pari a  /2, con la tensione
che è in anticipo rispetto alla corrente. La legge di Ohm diventa:
V = j XL I
Dove V ed I sono vettori, mentre XC si considera costante se la frequenza è costante. j è un
operatore matematico che applicato alla corrente la sfasa di 90° in anticipo, quindi V che si ottiene
moltiplicando la corrente per j è in anticipo di 90° rispetto alla corrente.
CIRCUITO PURAMENTE CAPACITIVO
Un circuito si dice puramente capacitivo quando sono presenti solo condensatori. Lo schema
elettrico è il seguente:
Puramente capacitivo
Condensatore
(CH1)
canale
1
G
~
R
2
(CH2)
canale
2
Resistenza
ausiliaria
ITI SAVIGNANO RELAZIONE N.4Rilievo
IM
  90o
V
dello sfasamento tra tensione (V) e intensità (I) Pag.5
Puramente capacitivo
VM
t
IM
In pratica il condensatore è costretto a caricarsi, scaricarsi e caricarsi di segno opposto seguendo la
tensione alternata applicata ai suoi capi. Si dice reattanza capacitiva l'ostacolo che il condensatore
oppone al passaggio della corrente alternata. La reattanza capacitiva si indica col simbolo XC, si
misura in  , si calcola con la seguente formula:
XC = 1/  C
Tale formula ci dice che la reattanza del condensatore avente capacità C è pari all'inverso del
prodotto della pulsazione per la capacità C del condensatore. Dove  = 2  f.
Tra tensione e corrente nel condensatore esiste uno sfasamento di 90° , pari a  /2, con la corrente
che va in anticipo rispetto alla tensione. La legge di Ohm diventa:
V = - j XC I
Dove V ed I sono vettori, mentre XC si considera costante se la frequenza è costante. j è un
operatore che applicato alla corrente la sfasa di 90° in anticipo, poiché però compare il segno - la
sfasa in ritardo di 90°, di conseguenza la tensione è in ritardo di 90° rispetto alla corrente.
PREPARAZIONE DELL’ESPERIENZA
ITI SAVIGNANO RELAZIONE N.4Rilievo
dello sfasamento tra tensione (V) e intensità (I) Pag.6
In questa esperienza ho preparato una serie di circuiti in cui dovevo verificare lo sfasamento della
corrente tramite l’oscilloscopio:
Il primo circuito che ho costruito era puramente resistivo, dal generatore di onde sinusoidali, con un
connettore a T ho sdoppiato i cavi coassiali; si va con un cavo a ch1 (quello che genera l’onda della
V) poi da CH1 vado alla resistenza R1, mentre con l’altro cavo mi collego alla massa. Dal CH2
esco con il cavo e vado su R2 (resistenza ausiliaria che serve per determinare una I 
determina
V
) e
R
l’intensità di corrente rappresentata dalla curva che inizialmente sta sotto (nello
schermo) ,infine chiudo il circuito sulla massa;
Il secondo circuito che era puramente induttivo, quindi non ho fatto altro che sostituire la resistenza
con un induttanza L;
Nel terzo circuito che era puramente capacitivo ho sostituito l’induttanza L con un condensatore C
DESCRIZIONE DELL’ESPERIENZA:
in questa esperienza, allo ho determinato lo sfasamento tra tensione e intensità di corrente, ho
preparato una serie di circuiti, poi ho visualizzato l’andamento delle due grandezze, sullo schermo
dell’oscilloscopio, studiandone gli effetti causati dalle resistenze e dai condensatori. Sullo schermo
dell’oscilloscopio le onde sinusoidali prima, quella della tensione, quando la corrente entra, tramite
CH 1, nell’oscilloscopio. La seconda si forma quando la corrente attraversa R2, e mi crea un onda,
che rappresenta la corrente, che viene visualizzata sotto alla prima onda. Una volta visualizzate le
due onde con degli appositi pomelli e delle regolazioni muovendo le onde sia sull’asse x che y ho
cercato di farla combaciare per vedere se vi era uno sfasamento o no.
CONCLUSIONI: l’esperienza che ho effettuato ho sottoposto 3 circuiti ad una tensione costante
che aveva una frequenza di 40 kHz ed attraversati da una corrente alternata, allo scopo di verificare
qual era lo sfasamento, delle diverse impedenze sulla corrente. Nella prova ho confrontato le
diverse onde sinusoidali alternate come la V e la I. Nel primo circuito (resistivo) sovrapponendo le
due curve, sullo schermo, si nota che non hanno sfasamento, cioè nessuna traslazione sull’asse “x”;
si eguagliano come frequenza, anche se hanno un’ampiezza diversa, quindi una resistenza posta in
un circuito, nel nostro caso, non va ad influire sull’andamento della corrente e le due grandezze
rimangono in fase. Nel secondo circuito (induttivo) sovrapponendo le curve si notava una
traslazione della sinusoide, rappresentante la corrente, di

(90o) sull’asse “x”, in ritardo rispetto a
2
quella della tensione. I rapporti fra le curve sono sempre: uguali frequenze, ampiezza V  I . Se
inserisco un solenoide (o bobina) in un circuito, , la tensione continua il suo corso naturale, L crea
ITI SAVIGNANO RELAZIONE N.4Rilievo
dello sfasamento tra tensione (V) e intensità (I) Pag.7
una resistenza che provoca un effetto di ritardo sull’intensità di corrente che viene ostacolata.,
quindi se aumentassimo L aumenterebbe anche XL ma poi viene diminuita I (perché I = V/ XL).
inoltre se aumento la frequenza mi diminuisce la I (perché X L = 2*f), quindi un solenoide fa
passare meglio le frequenze basse e blocca maggiormente quelle alte. Nell’ultimo circuito
(capacitivo) facendo coincidere le curve si è vista una traslazione, della corrente sull’asse delle X in
anticipo di 90o (

) rispetto all’onda sinusoidale che rappresenta la tensione. Le due curve hanno la
2
stessa frequenza ma varia l’ampiezza fra V e I. Inserendo un condensatore in un circuito e
aumentando C mi diminuisce XC (perché X C 
1
) quindi mi aumenta la corrente I, quindi i
 *C
condensatori fanno passare con più facilità le frequenze alte, e con difficoltà quelle basse
ITI SAVIGNANO RELAZIONE N.4Rilievo
dello sfasamento tra tensione (V) e intensità (I) Pag.8