1
RACCOLTA DI ESERCIZI
1) Deflessione elettrostatica
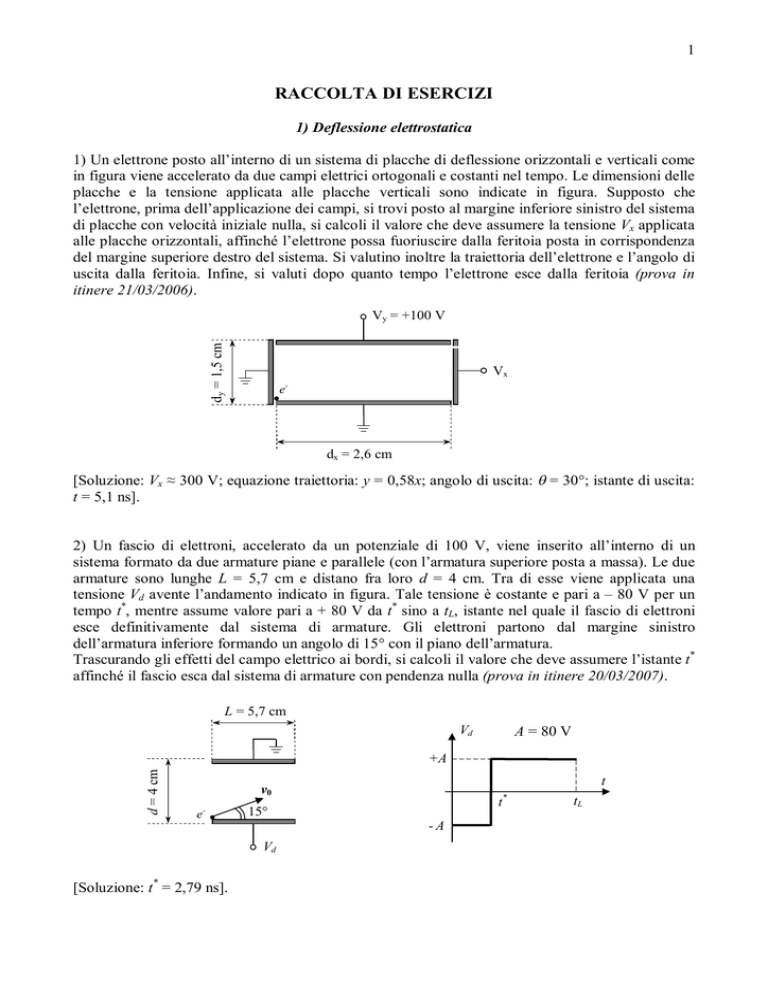
1) Un elettrone posto all’interno di un sistema di placche di deflessione orizzontali e verticali come
in figura viene accelerato da due campi elettrici ortogonali e costanti nel tempo. Le dimensioni delle
placche e la tensione applicata alle placche verticali sono indicate in figura. Supposto che
l’elettrone, prima dell’applicazione dei campi, si trovi posto al margine inferiore sinistro del sistema
di placche con velocità iniziale nulla, si calcoli il valore che deve assumere la tensione Vx applicata
alle placche orizzontali, affinché l’elettrone possa fuoriuscire dalla feritoia posta in corrispondenza
del margine superiore destro del sistema. Si valutino inoltre la traiettoria dell’elettrone e l’angolo di
uscita dalla feritoia. Infine, si valuti dopo quanto tempo l’elettrone esce dalla feritoia (prova in
itinere 21/03/2006).
dy = 1,5 cm
Vy = +100 V
Vx
e
-
dx = 2,6 cm
[Soluzione: Vx ≈ 300 V; equazione traiettoria: y = 0,58x; angolo di uscita: = 30°; istante di uscita:
t = 5,1 ns].
2) Un fascio di elettroni, accelerato da un potenziale di 100 V, viene inserito all’interno di un
sistema formato da due armature piane e parallele (con l’armatura superiore posta a massa). Le due
armature sono lunghe L = 5,7 cm e distano fra loro d = 4 cm. Tra di esse viene applicata una
tensione Vd avente l’andamento indicato in figura. Tale tensione è costante e pari a – 80 V per un
tempo t*, mentre assume valore pari a + 80 V da t* sino a tL, istante nel quale il fascio di elettroni
esce definitivamente dal sistema di armature. Gli elettroni partono dal margine sinistro
dell’armatura inferiore formando un angolo di 15° con il piano dell’armatura.
Trascurando gli effetti del campo elettrico ai bordi, si calcoli il valore che deve assumere l’istante t*
affinché il fascio esca dal sistema di armature con pendenza nulla (prova in itinere 20/03/2007).
L = 5,7 cm
Vd
A = 80 V
d = 4 cm
+A
t
v0
e-
t
15°
-A
Vd
[Soluzione: t* = 2,79 ns].
*
tL
2
3) Un elettrone posto sulla placca inferiore di un sistema di deflessione elettrostatica, avente
un’energia cinetica iniziale E0 = 1,6·10-16 J, è diretto verticalmente verso la placca superiore.
a. Se tra le due placche (distanti tra loro di un valore d) è
applicato un potenziale VD di 800 V, con il potenziale maggiore
applicato alla placca inferiore come mostrato in figura,
l’elettrone può raggiungere il secondo elettrodo? In caso
affermativo, con quale velocità?
d
VD
b. Quale valore deve avere VD affinché l’elettrone raggiunga
E0
+
l’elettrodo superiore con velocità nulla?
c. Se si triplica la distanza d tra le due placche, l’elettrone
riesce a raggiungere la placca superiore?
(prova in itinere 18/03/2008).
[Soluzione: a. L’elettrone riesce a raggiungere il secondo elettrodo con velocità finale 8,39·106 m/s.
È facile mostrare che
E0 eVD l' elettrone raggiunge l' elettrodo (con energia finale E f 0)
E0 eVD l' elettrone raggiunge l' elettrodo con velocità finale nulla ( E f 0)
E eV
l' elettrone non raggiunge l' elettrodo ( E f 0)
D
0
b. VD = 1000 V
c. Il fatto che l’elettrone riesca a raggiungere o meno l’elettrodo superiore è indipendente dalla
distanza tra gli elettrodi d].
4) Progettare un sistema di deflessione elettrostatica avente le seguenti caratteristiche:
- deflessione verticale massima sullo schermo: D = 5 cm;
- massima tensione applicata alle placchette di deflessione: V = 500 V;
- massima frequenza del segnale analizzabile: f = 20 MHz;
- velocità iniziale con la quale il fascio di elettroni entra all’interno del sistema di deflessione:
v0 = 1,875 m/s (prova in itinere 24/03/2009).
[Soluzione: Si dimostra che: l/d < 2 e, posto ttr = T/20, si ricava l = 4,7 cm, Posto d = 3 cm, si
ottiene L = 12,8 cm, avendo posto: l lunghezza delle placchette, d distanza tra le placchette, ttr
tempo di transito dell’elettrone all’interno delle placchette, T periodo del segnale da analizzare, L
distanza tra il centro delle placchette e lo schermo].
5) Determinare il minimo valore di tensione
Vd, da applicare al sistema mostrato in figura,
costituito da due armature piane e parallele
distanti d = 5 mm, affinché un elettrone,
iniettato all’interno del sistema con un
potenziale di accelerazione di 200 V e un
angolo di 45°, viaggi all’interno dello spazio
delimitato dalle armature senza urtare contro
l’armatura superiore.
–
y
0.5 mm
v0
θ = 45°
d = 5 mm
x
+
3
L’elettrone parta ad una distanza di 0,5 mm dall’armatura inferiore, posta ad un potenziale positivo
rispetto all’armatura superiore (prova in itinere 19/03/2010).
[Soluzione: Vd = 111 V].
6) In un sistema di armature piane e parallele distanti d = 1 cm, viene applicata una tensione, il cui
andamento è rappresentato in figura. Nell’ipotesi che il potenziale venga applicato all’elettrodo
superiore, si determini se un elettrone, posto inizialmente sull’armatura inferiore con velocità
iniziale nulla, può raggiungere l’armatura superiore, oppure ricade sull’armatura inferiore prima di
giungere a quella superiore (prova in itinere 12/04/2011).
VD [V]
500
t [ns]
0
1
[Soluzione: L’elettrone non raggiunge l’armatura].
2
4
2) Fisica dei semiconduttori
1) A seguito di un repentino aumento di temperatura, il livello di Fermi EF di una barretta di silicio
di tipo p si sposta di 0,159 eV rispetto al valore che esso aveva a temperatura ambiente, distando
adesso 0,191 eV dal livello di Fermi Ei intrinseco. Si calcoli l’avvenuta variazione di temperatura
(per semplicità, soltanto nell’espressione della concentrazione di cariche intrinseche ni alla nuova
temperatura, si assuma che l’energia della gap proibita sia diminuita del 6%, mentre NC e NV siano
raddoppiati rispetto ai valori a temperatura ambiente). Si verifichi infine, che alla nuova
temperatura sia ancora possibile trascurare le cariche generate termicamente, ai fini del calcolo delle
cariche maggioritarie (prova in itinere 21/03/2006).
[Soluzione: T = Tfinale – Tamb = 172 K (cioè Tfinale = 199°C)].
2) Una barretta di silicio di tipo p, avente le dimensioni riportate in figura, ha una resistività al buio
b di 8 ∙cm a temperatura ambiente. La barretta viene illuminata uniformemente da una sorgente
in grado di generare 3∙1019 coppie elettrone-lacuna al cm3 e al s, con un tempo di vita medio delle
cariche di 10 s. La barretta è inserita in un circuito partitore in grado di rilevare le variazioni di
resistenza della barretta come variazioni di tensione (misurate tramite il voltmetro in parallelo
all’uscita). Calcolare la variazione di tensione in uscita del circuito a seguito dell’irradiazione della
barretta, considerando soltanto i valori a regime. Si calcoli nuovamente la variazione di tensione al
variare delle condizioni di illuminazione, se la barretta è mantenuta ad una temperatura costante di
450°C. Si consideri la mobilità proporzionale a T -1,5, essendo T la temperatura espressa in gradi
Kelvin (prova in itinere 21/03/2006).
V= +10 V
c
b
a
R
V
a = 1 cm
b = 1 mm
c = 1 mm
R = 800
[Soluzione: A temperatura ambiente: NA = 1,65·1015 cm-3, p = 475 cm2/(V·s), n = 1225 cm2/(V·s),
l = 4,83 ·cm, V = 1,2 V. Alla temperatura T = 723 K: p = 127 cm2/(V·s), n = 327 cm2/(V·s),
b= 0,6 ·cm,l = 0,59 ·cm, V ≈ 0 V].
3) Un resistore integrato di forma quadrata di lato pari a 100 m è ottenuto da uno strato di silicio di
tipo p spesso 1 m. Sapendo che la sua resistenza, misurata a temperatura ambiente, è pari a 10 k,
calcolate il valore che tale resistenza assume a 150°C e a 500°C, supponendo che la mobilità resti
costante con la temperatura. Si giustifichino i risultati ottenuti effettuando appropriate
considerazioni fisiche (prova in itinere 20/03/2007).
5
[Soluzione: NA = 1,67·1016 cm-3, p = 375 cm2/(V·s), n = 925 cm2/(V·s), R(150°C) = 10 k,
R(500°C) = 1,22 k].
4) Una barretta di silicio, drogata con 2,1∙1015 atomi di fosforo per cm3, è esposta ad una radiazione
in grado di generare 5∙1019 coppie elettrone-lacuna per cm3 e per secondo all’interno della barretta.
Se la sorgente di radiazione viene spenta, si calcoli la concentrazione di cariche minoritarie nella
barretta, 4 s e 40 s dopo l’istante di spegnimento, assumendo che il tempo di vita media dei
portatori minoritari è pari a 2 s. Commentate i risultati ottenuti (prova in itinere 11/04/2007).
[Soluzione: pn(4 s) = 1,35·1013 cm-3, pn(40 s) = 3·105 cm-3].
5) Una barretta di silicio è drogata con atomi di boro e di fosforo. Sapendo che il semiconduttore è
di tipo n, che alla temperatura di 250°C la concentrazione di elettroni liberi è pari a 1017 cm-3 e che
la resistività è pari a 3,84·10-1 ·cm, si calcoli la concentrazione di atomi accettori NA e quella di
atomi donatori ND. Si consideri la mobilità proporzionale a T -1,5 (prova in itinere 18/03/2008).
[Soluzione: ND = 3·1017 cm-3, NA = 2·1017 cm-3].
6) Un wafer di silicio di tipo n è tale che il suo livello di Fermi disti dal livello intrinseco di una
quantità EF – Ei = 0,378 eV a temperatura ambiente. Il wafer viene illuminato uniformemente in
modo tale che l’illuminazione produca la generazione di 1022 coppie elettrone-lacuna al cm3 e al s,
con un tempo di vita medio di elettroni e lacune pari a 1 s. Determinare il valore della resistività a
regime durante l’illuminazione (prova in itinere 18/03/2008).
[Soluzione: L = 0,177 ·cm].
7) Un resistore integrato di forma quadrata di lato pari a l è ottenuto da uno strato di silicio di tipo p
spesso 10 m e la sua resistenza, misurata a temperatura ambiente, è pari a 10 k. Drogando
ulteriormente il resistore con drogante di tipo n, la resistenza diviene pari a 1 k. Calcolare le
concentrazioni dei due drogaggi NA e ND (prova in itinere 24/03/2009).
[Soluzione: ND = 7,2·1015 cm-3, NA = 1,3·1015 cm-3].
8) In una barretta di silicio drogata in modo perfettamente compensato, la resistività a temperatura
ambiente è pari a 3,08·105 ·cm. Si determini la concentrazione di droganti accettori e donatori.
La resistività della barretta di silicio così compensato risulta maggiore o minore rispetto a quella
di un’uguale barretta di silicio intrinseco? Giustificare la risposta (prova in itinere 19/03/2010).
[Soluzione: ND = NA = 5·1015 cm-3. Per il silicio intrinseco: i = 2,35·105 ·cm. Nel caso
compensato la resistività è maggiore, in quanto le mobilità di elettroni e lacune sono minori].
9) Data una barretta di silicio mantenuta a temperatura ambiente, drogata con una concentrazione di
atomi di fosforo pari a 1016 cm–3 e di atomi di boro pari a 1015 cm–3, si determini l’espressione
analitica della concentrazione delle cariche minoritarie nel tempo, supponendo che all’istante t = 0
6
essa venga illuminata uniformemente da una radiazione di colore rosso in grado di generare 5·1020
coppie elettrone-lacuna al cm–3 e al secondo. Si assuma un tempo di vita medio per elettroni e
lacune pari a 2 s.
Si diagrammi l’andamento della concentrazione di cariche minoritarie nel tempo, evidenziando
in particolare l’incremento del valore della concentrazione a regime rispetto al valore in equilibrio.
Come varierebbe l’andamento della suddetta concentrazione, se la radiazione fosse nel medio
infrarosso? (prova in itinere 07/04/2010).
[Soluzione: p n (t ) p n 0 G L p 1 e
t p
2,3 10
4
1015 1 e t
210 6
.
p n (t )
4,3 1010 .
pn0
Nel medio infrarosso la radiazione non viene assorbita dal silicio, per cui si ha: p n (t ) p n0 ].
Incremento
10) Una barretta di silicio è drogata con fosforo, la cui proporzione in peso è pari a
1,03·10–7 g/cm3. Si calcoli la sua resistività.
Al fine di diminuire la sua resistività del 50%, si calcoli rispettivamente:
a) di quanto si deve incrementare in percentuale la proporzione in peso di fosforo;
b) quale deve essere la velocità di generazione della concentrazione di cariche, nell’ipotesi di
illuminare la barretta con una radiazione luminosa tale da essere completamente assorbita dal
semiconduttore. Si consideri in questo caso un tempo di vita medio per elettroni e lacune uguale a
1 s (Suggerimento: Si consideri iniezione ad alto livello) (prova in itinere 12/04/2011).
[Soluzione: a) L’incremento è circa 115%. b) GL = 1,44·1021 cm-3s-1].
7
3) Diodo a giunzione
1) Con riferimento al circuito limitatore in figura analizzarne il funzionamento, considerando di
ricavare la tensione di riferimento VR = 2 V da un partitore R1- R2 connesso ad un alimentatore da
10 V e tale che la somma delle resistenze sia pari a 10 k. Supponendo di applicare in ingresso un
segnale sinusoidale di ampiezza massima pari a 5 V, tracciare la transcaratteristica e le forme
d’onda d’ingresso e d’uscita. Si trascuri la resistenza dinamica del diodo e si assuma una tensione di
soglia pari a 0,6 V.
Considerando nuovamente il partitore sul ramo del diodo, si dimensionino le resistenze del
partitore in modo che, mantenendo gli stessi valori per VR e per la tensione d’alimentazione, la
tensione d’uscita resti sempre limitata a valori inferiori a 3 V (prova in itinere 10/04/2006).
R
D
+
vi
vo
VR
R = 1 k
VR = 2 V
[Soluzione:
D OFF per vi ≤ VR + V = 2,6 V vo = vi.
Req
D ON per vi ≥ 2,6 V vo V R V
vi VR V 0,615vi 1 ,
R Req
dove Req = R1//R2 = 1,6 k.
Affinché vo ≤ 3 V deve essere
Req
R Req
0,167 Req 200 , dove 0,167 è il coefficiente
angolare della retta per vi ≥ 2,6 V; inoltre deve essere
R2
10 VR
R1 R2
R2
0,2 .
R1 R2
Scegliendo R1 = 500 R2 = 125 ].
2) Si consideri l’onda quadra in figura di ampiezza 0-6,5 V; il livello alto di tale onda è affetto da
rumore le cui fluttuazioni variano di ±20% rispetto al valore nominale. Si progetti un regolatore di
tensione a diodo Zener che permetta di eliminare tali fluttuazioni stabilizzando la tensione ad un
valore più basso di quello nominale. La potenza massima dissipabile dal diodo sia pari a ½ W. Si
verifichi che la corrente sullo Zener non sia mai più bassa di 1 mA.
Inoltre si stabiliscano i drogaggi di tale diodo, supponendo che la giunzione sia di tipo p++-n (con
NA pari almeno a 100 ND) e che il campo elettrico critico sia uguale a 5∙105 V/cm (prova in itinere
10/04/2006).
8
vi
6,5 V + 20%
6,5 V
6,5 V - 20%
t
[Soluzione:
vi (MAX) V Z
(6,5 1,3) 5
28 . Scegliamo RS = 56 .
I Z (MAX)
100 10 3
Con questo valore, la massima corrente IZ che circolerà sul diodo è 50 mA, mentre la minima è
3,6 mA (> 1 mA, come richiesto).
Progetto del diodo: ND = 1,2·1017 cm-3 e NA = 1,2·1019 cm-3].
Nel peggiore dei casi deve essere: R S
3) Lo schema in figura rappresenta un sistema in grado di far funzionare un orologio elettronico
(che deve essere alimentato con tensioni comprese tra 12 V e 15 V) anche nel caso in cui venga a
mancare l’alimentazione esterna di rete. Proporre un semplice schema elettrico del circuito
d’interfaccia, che permetta di commutare automaticamente le due alimentazioni, in base alla
presenza o meno dell’alimentazione di rete (prova in itinere 10/04/2006).
ALIMENTAZIONE DI RETE
(FILTRATA)
INTERFACCIA
+12V ÷ +15 V
?
15 V
220 V
-
OROLOGIO
+
BATTERIA
12 V
[Soluzione:
vs. orologio ].
+15 V
+12 V
4) Sapendo che la corrente inversa di diffusione di un diodo a giunzione al silicio è pari a
100 pA quando la temperatura è uguale a 100°C, si calcolino i valori dei tempi di vita media delle
cariche minoritarie n e p nell’ipotesi che:
p = 2n,
n e p siano indipendenti dalla temperatura,
9
l’area della sezione del diodo sia 1 mm2,
i drogaggi delle zone p e n valgano nell’ordine NA = 2∙1018 cm-3 e ND = 2∙1017 cm-3,
la mobilità delle cariche diffuse sia inversamente proporzionale alla temperatura.
Si valuti inoltre come varia la lunghezza di diffusione delle cariche minoritarie con la
temperatura (prova in itinere 11/04/2007).
[Soluzione: n = 111 ns, p = 222 ns; Lp,n indipendenti dalla temperatura].
5) Si rappresenti in scala la transcaratteristica vo / vi del seguente circuito a diodi (considerati ideali
con V = 0) (prova in itinere 11/04/2007).
R1
vi
+
D1
D2
R1 = R2 = R3 = R4 = 10 k
VR = 10 V
R4
R2
R3
vo
VR
[Soluzione:
vi ≤ 10 V vo = 5 V (D1 OFF, D2 ON);
10 V ≤ vi ≤ 30 V vo = 0,25 vi + 2,5 (D1 ON, D2 ON);
vi ≥ 30 V vo = 10 V (D1 ON, D2 OFF) ].
6) In un diodo Zener i drogaggi delle zone p e n sono rispettivamente NA = 1017 cm-3 e
ND = 6·1017 cm-3. Sapendo che il campo elettrico in corrispondenza del breakdown è uguale a
3·105 V/cm, calcolare la tensione di Zener del diodo a temperatura ambiente e a 350°C (prova in
itinere 08/04/2008).
[Soluzione: VZ(Tamb) = 2,53 V, VZ(400°C) = 2,96 V].
7) Per il circuito in figura si calcolino la tensione e
la corrente sul carico RL nei tre casi seguenti:
Caso 1
Caso 2
Caso 3
deviatore A
posizione 0
posizione 1
posizione 1
deviatore B
indifferente
posizione 0
posizione 1
Sia R1 = R2 = RL = 1 k, E1 = 1,5 V e
E2 = –6 V. I diodi D1 e D2 si considerino ideali con
tensione di soglia V = 0,6 V (prova in itinere
08/04/2008).
E2
0
1
R2
A
R1
D2
IL
3V
0
B
1
Vi
D1
VL
RL
E1
3V
[Soluzione: Caso 1 (Vi = 0 V): VL = –1,5 V; IL = –1,5 mA. Caso 2 (Vi = 3 V): VL = –0,6 V; IL =
= –0,6 mA. Caso 3 (Vi = 6 V): VL = 0 V; IL = 0 A].
10
8) a. Dopo aver determinato lo stato dei diodi al variare della tensione d’ingresso vi, tracciare la
transcaratteristica del seguente circuito, sapendo che R1 = R2 = R3 = 1 k e VR = 5 V. I diodi D1 e
D2 si considerino ideali con tensione di soglia V = 0,6 V.
b. Come si modifica la transcaratteristica se R1 = R2 = R3 = 100 k e VR = 15 V?
c. Si tracci nuovamente la transcaratteristica del circuito, considerando vi generatore di tensione non
ideale, avente resistenza interna Rs = 600 (prova in itinere 16/04/2009).
D1
A
D2
B
C
R1
vi
vo
R3
R2
VR
[Soluzione: a. vi ≤ 0,6 V D1 OFF, D2 OFF e si ha vo = 0 V ;
0,6 V ≤ vi ≤ 1,2 V D1 ON, D2 OFF ma si ha ancora vo = 0 V ;
vi ≥ 1,2 V D1 ON, D2 ON e si ha vo = vi – 1,2 .
b. La transcaratteristica è indipendente da R1, R2, R3 e VR.
c. vi ≤ 3,96 V D1 OFF, D2 OFF e si ha vo = 0 V ;
3,96 V ≤ vi ≤ 4,92 V D1 ON, D2 OFF ma si ha ancora vo = 0 V ;
vi ≥ 4,92 V D1 ON, D2 ON e si ha vo = 0,625 vi – 3,075 ].
9) Dopo aver determinato lo stato dei diodi al variare della tensione in ingresso vi, si tracci la
transcaratteristica del circuito in figura e si diagrammi la tensione d’uscita nei due casi in cui la
tensione d’ingresso sia vi1 = 3 sen ( t) e vi2 = 7 sen ( t). I diodi si considerino ideali con tensione di
soglia V = 0,6 V (prova in itinere 07/04/2010).
D1
vi
+
D2
D3
D4
V1
R1 = R2 = 1 k
V1 = 1 V
V2
vo
R1
R2
V2 = 2 V
[Soluzione:
Per vi ≤ 4,4 V vo = 2 V ;
per vi ≥ 4,4 V vo = vi – 2,4
vo
vo2
4,6
2
vo1
t
].
11
10) Dato il seguente circuito si indichi nel piano E1 – E2 la regione entro la quale il diodo D si trova
in conduzione.
Il diodo si consideri ideale, con tensione di soglia pari a V = 0,6 V V (prova in itinere
05/05/2011).
R3
R1
R1 = 2 k
R2 = 3 k
D
R2
E1
E2
R3 = 1 k
[Soluzione:
E2 [V]
D ON
0,6
E1 [V]
].
–1
11) Nel circuito in figura:
a) si calcoli il rapporto che deve sussistere tra le resistenze R1 e R2 del potenziometro, affinché
il diodo D si trovi in conduzione;
b) posto R1 = 3 R2, si calcoli il valore delle suddette resistenze affinché la corrente sul diodo sia
pari a 0,5 mA;
c) si valuti in che posizione deve trovarsi il potenziometro affinché il diodo D dissipi la
massima potenza possibile; in tale condizione si calcoli altresì il valore di tale potenza dissipata.
In tutti i casi, il diodo si consideri ideale, con tensione di soglia pari a V = 0,6 V V (prova in
itinere 05/05/2011).
E1
R1
R2
R
D
E2
R = 1 k
E1 = 4 V
E2 = 2,6 V
[Soluzione: a. R2/R1 ≤ 1; b. R1 = 4 k, R2 = 1,33 k; c. R2 = 0, P = 1,2 mW].
12
12) Si stabilisca lo stato dei due diodi D1 e D2 nel circuito che segue, calcolando inoltre il valore
della tensione al nodo U e le correnti sui due diodi.
I due diodi si considerino ideali, con tensione di soglia pari a V = 0,6 V (prova in itinere
05/05/2011).
+E1
D1
R1
D2
R2
+E2
U
R3
R1 = 1 k
R2 = 1 k
R3 = 7,4 k
E1 = +7 V
E2 = +9 V
[Soluzione: D1 OFF, D2 ON].
13) Si progetti la resistenza di polarizzazione RS dello stabilizzatore di tensione in figura, sapendo
che:
RS
- il carico è costituito da una resistenza
RL di 100 ;
- la tensione da stabilizzare E è pari a
+
12 V;
DZ
- il diodo Zener ha una tensione di
E
vo
RL
Zener pari a VZ = 10 V, una corrente minima
di Zener (corrente di ginocchio) IZK = 2 mA
e può dissipare una potenza massima di 1 W
(prova in itinere 06/06/2011).
[Soluzione: 10 ≤ RS ≤ 20 ].
13
4) Transistor ad effetto di campo (FET)
1) Si dimensionino le resistenze del circuito in figura, sapendo che il punto di riposo del MOSFET
è ID = 2,5 mA, VDS = 5,5 V e VGS = -1 V; inoltre K = 2,5 mA/V2 e la tensione sul source è VS = 6 V
(prova in itinere 19/05/2006).
+VDD
RD
R1
Ro
RL = 25 k
VDD = 20 V
CL
Ci
vo
+
vs
vi
CS
R2
RS
RL
RS1
RS2
[Soluzione: RS = 2,4 k, RD = 3,4 k, R1 = 1,5 M, R2 = 500 k,].
2) Per il circuito del precedente esercizio, si ricavi il valore delle resistenze del potenziometro RS1 e
RS2 affinché l’amplificazione di tensione Av = vo/vi sia uguale a -1,5.
Se la transconduttanza gm aumentasse di un fattore 5 quanto varierebbe grossomodo
l’amplificazione Av?
Si calcoli infine la resistenza d’uscita del circuito (prova in itinere 19/05/2006).
[Soluzione: RS2 = 1,8 k(se si suppone gmRS2 » 1, si ottiene RS2 = 2 k) e RS1 = RS – RS2 = 600 .
Se gm aumentasse di un fattore 5, l’amplificazione rimarrebbe pressappoco la stessa dato che
R // R D
Av ≈ L
, cioè è indipendente da gm. Resistenza d’uscita Ro = RD = 3,4 k].
RS
14
3) Si calcolino le correnti I1, I2 e la tensione Vo del seguente circuito
+9V
M2
Z1 = Z2 = 10 m
L1 = L2 = 1 m
n = 500 cm2/(V∙s)
p = 200 cm2/(V∙s)
dox = 10 nm
ox = 3,45∙10-13 F/cm
|Vt1| = |Vt2| = 1 V
I2
I1
Vo
M1
dove Z1 e Z2 indicano le larghezze del canale dei due MOSFET ad arricchimento, L1 e L2 le
lunghezze del canale, n e p le mobilità del canale dell’NMOS e del PMOS rispettivamente, dox lo
spessore dell’ossido di gate, ox la costante dielettrica del biossido di silicio, Vt1 e Vt2 le tensioni di
soglia dei due MOSFET (prova in itinere 23/05/2007).
[Soluzione: I1 = I2 = 5 mA; Vo = 3,41 V].
4) Dopo aver determinato il punto di riposo del MOSFET ad arricchimento, si calcolino
l’amplificazione di tensione e le resistenze d’ingresso e d’uscita del circuito in figura. Per il
MOSFET si consideri K = 1 mA/V2 e Vt = 1 V.
Si considerino trascurabili la resistenza d’uscita del dispositivo ro e le reattanze dei condensatori
alla frequenza di funzionamento del circuito; si tenga invece conto della presenza della resistenza
RG (prova in itinere 23/05/2007).
+E
RD
RG
Ci
Co
vo
E = 15 V
RD = 3 k
RG = 390 k
vi
[Soluzione: Punto di riposo: ID = 4 mA; VDS = VGS = 3 V. Amplificazione: Av ≈ – 12. Resistenza
d’ingresso: Ri ≈ 30 k. Resistenza d’uscita: Ro = RD // RG ≈ RD = 3 k].
15
5) Si calcolino la corrente Io e la tensione Vo del seguente circuito
+VDD
M2
VDD = 5 V
K1 = K2 = 1 mA/V2
Io
|Vt1| = |Vt2| = 1 V
Vo
M1
dove K1 e K2 indicano i parametri di conducibilità e Vt1 e Vt2 le tensioni di soglia dei due MOSFET
(prova in itinere 21/05/2008).
[Soluzione: Io = 0 A; Vo = 0 V].
6) Si dimensionino le resistenze del circuito in figura, nell’ipotesi che:
il parametro di conducibilità e la tensione di soglia del MOSFET ad arricchimento siano
rispettivamente K = 1 mA/V2 e Vt = 2 V;
il punto di riposo del MOSFET sia ID = 4 mA e VDS = 8 V;
l’amplificazione di tensione del circuito sia pari a Av = – 4;
la resistenza d’ingresso del circuito sia pari a Ri = 1 M.
Si considerino trascurabili la resistenza d’uscita del dispositivo ro e le reattanze dei condensatori
alla frequenza di funzionamento del circuito (prova in itinere 21/05/2008).
+ VDD
RD
R1
VDD = 15 V
Co
Ci
RL = 100 k
vo
vi
R2
RS
RL
CS
[Soluzione: RD = 1 k; RS = 750 ; R1 = 2,1 M; R2 = 1,875 M].
16
7) a. Dimensionare le resistenze R1 e R2 del circuito di figura affinché l’NMOS a svuotamento
risulti polarizzato in zona di saturazione con una corrente ID = 4 mA e la potenza erogata dal
generatore VDD sia minore di 61 mW. Per il MOSFET si consideri Vt = – 2 V e IDSS = 4 mA.
b. Considerando trascurabili la resistenza d’uscita del MOSFET ro e le reattanze dei condensatori
alla frequenza di funzionamento del circuito, si calcoli l’amplificazione di tensione Av = vo / vi, la
resistenza di ingresso Ri e di uscita Ro del circuito (prova in itinere 19/05/2009).
VDD
R1
VDD = 15 V
RD
RD = RS = RL = 1 kΩ
C
C
RL
C
R2
RS
Rin
Rout
[Soluzione: a. R1 = 220 k; R2 = 80 k, scegliendo una corrente su R1 pari a 50 A. b.
Amplificazione: Av = 2. Resistenza d’ingresso: Ri = 200 . Resistenza d’uscita: Ro = 1 k].
8) Tra i circuiti riportati di seguito in figura, solo uno è correttamente funzionante ed adatto a
realizzare un amplificatore.
+ VDD
+ VDD
+ VDD
R1
RD
RD
RD
b
c
– VGG
RG
RG
R2
a
RS
17
+ VDD
RD
R1
– VDD
+ VDD
RD
RD
f
RG
RG
d
e
RS
R2
Si individui tale circuito e si spieghi il motivo per il quale esso è polarizzato correttamente, mentre
gli altri non possono funzionare. Per ogni circuito si dia un spiegazione qualitativa ma chiara ed
esauriente.
Si calcoli il punto di riposo dell’unico circuito correttamente polarizzato, sapendo che per tutti i
circuiti si ha VDD = 9 V, VGG = 5 V, |Vt | = 1 V, K = 1 mA/V2. Inoltre, si abbia: R1 = 300 k,
R2 = 700 k, RG = 100 k, RD = 4 k, RS = 1 k (prova in itinere 19/05/2010).
[Soluzione: Circuito correttamente polarizzato: f. Punto di riposo: VGS = 0 V; ID = 1 mA;
VDS = 5 V].
9) Il circuito in figura è progettato in modo da fornire in uscita una tensione continua VO non nulla e
minore della tensione di alimentazione. Ad un certo istante, a causa di un guasto, la tensione
d’uscita si riduce a zero (VO = 0).
Si individui la possibile causa di guasto tra le seguenti sotto elencate, spiegandone il motivo.
+ VDD
a) R1 è cortocircuitata;
b) RD è cortocircuitata;
R1
RD
R2
RS
c) RD ha un terminale sconnesso dal circuito;
d) i terminali di drain e source del MOSFET sono
cortocircuitati;
e) il terminale di source è sconnesso dal circuito;
f) RS è cortocircuitata;
g) RS ha un terminale sconnesso dal circuito.
VO
18
Si giustifichi la scelta effettuata, spiegando perché le altre possibili cause sono da scartare (prova in
itinere 19/05/2010).
[Soluzione: Possibile causa di guasto: c (infatti, se RD sconnessa dal circuito, ID = 0 anche se
VGS > Vt, dunque VO = 0].
10) Si dimensionino le resistenze dell’amplificatore in figura, in modo che la corrente di drain a
riposo sia pari a ID = 2 mA, che la resistenza d’ingresso dell’amplificatore sia uguale a
Ri = 500 k e che il modulo dell’amplificazione di tensione sia |Av| = 10.
Per il MOSFET si abbia: K = 2 mA/V2 e Vt = 2 V.
Si consideri, infine, che la reattanza dei condensatori sia uguale a zero alla frequenza di
funzionamento del circuito (prova in itinere 19/05/2010).
+ VDD
RD
VDD = 12 V
Co
Ci
VGG = 4 V
+ VGG
+
vi
vo
RS
RG
CS
[Soluzione: RG = 500 k, RD = 2,5 k, RS = 500 ].
11) Si progetti un generatore di corrente utilizzando un JFET BF245B, le cui caratteristiche d’uscita
e la transcaratteristica sono riportate sotto in figura. Il generatore, alimentato con una tensione
VDD = +15 V, deve erogare una corrente pressoché costante di 10 mA su un carico RD variabile.
15
10
5
19
Qual è il massimo valore che può assumere il carico RD, affinché la corrente erogata risulti
costante. Si calcoli tale valore per via analitica, o per via grafica indifferentemente (prova in itinere
06/06/2011).
[Soluzione: RD ≤ 850 ].
12) Si calcolino le correnti I1, I2 e la tensione Vo del seguente circuito (prova in itinere 06/06/2011).
+ VDD
M2
VDD = 5 V
K1 = K2 = 1 mA/V2
I2
|Vt1| = |Vt2| = 1 V
I1
Vo
M1
[Soluzione: I1 = I2 = 1 mA; Vo = 0,41 V ].
20
5) Transistor bipolari a giunzione (BJT)
1) Per l’amplificatore riportato in figura si ha VCC = 10 VR1 = 10 kR2 = 2,2 kRE1 = 1 k
RC1 = 3,6 kR3 = 15 kR4 = 5 kRE2 = 1 k RC2 = 3,3 kRL = 1,5 keRs = 600 Per
entrambi i transistor si assuma = 100.
Determinare:
1)
il punto di riposo dei transistor;
2)
l’amplificazione di tensione AvT = vo/vs;
3)
l’andamento dei segnali nei punti A, B e C indicati nel circuito, specificando l’ampiezza,
il valore medio e la fase (rispetto al segnale d’ingresso) di ciascun segnale, nell’ipotesi
che il segnale d’ingresso sia una sinusoide a valor medio nullo di ampiezza 100 V.
Si trascurino le reattanze dei condensatori alla frequenza del segnale d’ingresso (prova in itinere
07/06/2006).
A, B, C
+VCC
?
R1
RC 1
?
RC 2
R3
C3
A
C2
C1
B
vo
C
Rs
vi
+
R2
RE
RE 1
CE 1
R4
2
RL
CE 2
vs
[Soluzione:
1) Punto di riposo: IC1 = 1,1 mA; VCE1 = 4,95 V; VB1 = 1,8 V; VC1 = 6,05 V; IC2 =
= 1,7 mA; VCE2 = 2,69 V; VB2 = 2,5 V; VC2 = 4,39 V.
2) Amplificazione: AvT = 1476.
3)
].
21
2) Si calcolino i punti di riposo dei transistor del seguente circuito considerando i due casi:
a) interruttore chiuso, b) interruttore aperto (prova in itinere 13/06/2007).
+VCC
R1
RC1
T2
T1
R2
RE1
RE2
VCC = 9 V
RC1 = 4,4 k
RE1 = 2,2 k
RE2 = 8,2 k
R1 = 129 k
R2 = 58 k
1 = 2 = 80
[Soluzione: a) Interruttore chiuso: VCE1 = 0,2 V; IC1 = 2 mA; IB1 = 50 A (T1 in saturazione);
VBE2 = 0,2 V; VCE2 = 9 V; IC2 = 0 mA; (T2 in interdizione). b) Interruttore aperto: VCE1 = 3,89 V;
IC1 = 0,78 mA; IB1 = 9,58 A; VCE2 = 4,11 V; IC2 = 0,6 mA; IB2 = 7,36 A (T1 e T2 in zona attiva)].
3) Al precedente circuito venga applicato un segnale d’ingresso costituito da una sinusoide a valor
medio nullo di ampiezza 50 mV e una resistenza di carico di valore pari a 200 k. Si determini
l’andamento del segnale nel punto S (indicato nel circuito di seguito riportato) nei due casi: a)
interruttore chiuso e b) interruttore aperto, specificandone l’ampiezza, il valore medio e la fase
(rispetto al segnale d’ingresso). Si trascuri la reattanza del condensatore C alla frequenza del
segnale d’ingresso.
Per determinare l’amplificazione complessiva del circuito si ricorra a semplici considerazioni
circuitali, senza disegnare lo schema equivalente dinamico (prova in itinere 13/06/2007).
RL = 200 k
vs = 50 sin( t)
(in mV)
22
[Soluzione:
a) Interruttore chiuso:
b) Interruttore aperto: AvT ≈ – RC1/RE1 = – 2; sfasamento segnale in uscita = 180°
].
4) L’interruttore I del circuito in figura controlla l’accensione e lo spegnimento del display a sette
segmenti. Esso è costituito da una schiera di sette diodi LED, aventi il terminale di catodo in
comune (CC) connesso al collettore del BJT. Dopo aver illustrato le modalità di funzionamento del
circuito, si dimensionino le resistenze R e RB del circuito nell’ipotesi che sul display – se acceso –
venga rappresentata la cifra “8” (cioè tutti i LED accesi). Si assuma una corrente di 10 mA in
ciascun LED (ILED) ed una corrispondente tensione di soglia (VLED) pari a 1,5 V. Il guadagno del
transistor sia pari a 100 (prova in itinere 11/06/2008).
R
R
+ VCC
R
RB
VCC = 5 V
ILED = 10 mA
VLED = 1,5 V
R
R
I
= 100
R
R
[Soluzione: Quando l’interruttore è chiuso il transistor è interdetto e tutti i LED sono spenti; invece
quando è l’interruttore è aperto tutti i LED si accendono. In quest’ultimo caso, supponendo il
transistor saturo con un fattore di overdrive pari a 3, si ricava: R = 330 e RB = 2 k].
5) Di seguito sono riportati alcuni maximum ratings (valori limite delle condizioni alle quali un
dispositivo può operare) estratti dai datasheet di cinque transistor disponibili in commercio
(2N3904, BF420, BF422, 2N2222, 2N2222A). Quali scegliereste o quali escludereste per realizzare
il circuito relativo all’esercizio 4 precedente? Si motivi la scelta effettuata (prova in itinere
11/06/2008).
23
2N3904
BF420-BF422
2N2222-2N2222A
[Soluzione: I BJT BF420 e BF422 non possono essere utilizzati in quanto per questi ultimi la
massima corrente di collettore è 50 mA, mentre nel transistor dell’esercizio 4, nel caso in cui tutti i
LED sono accesi, la corrente di collettore è 70 mA].
6) Dopo aver calcolato il punto di riposo del BJT si calcoli l’amplificazione di tensione
Av = vo / vi del circuito rappresentato sotto in figura, nei due casi: a) RB = 560 k,
b) RB = 100 . Il guadagno del BJT sia pari a 100.
Quale dei due valori di RB permette di ottenere un punto di riposo stabile? E quale dei due consente
di ottenere un’amplificazione di tensione tendente a quella tipica di una configurazione ad
emettitore comune? Si discutano brevemente i due casi (prova in itinere 11/06/2008).
24
+ VCC
VCC = 12 V
RC
RB
Ci
RC = 4,7 k
RE = 1,2 k
RL = 100 k
Co
vo
RL
= 100
vi
RE
CE
[Soluzione:
Punto di riposo. Caso a: IE = 0,98 mA; VCE = 6,19 V. Caso b: IE = 1,92 mA; VCE = 0,7 V.
Amplificazione: Caso a: Av = –177. Caso b: Av = –6,38.
VCC V BE
Si ha: I E
, pertanto il punto di riposo è stabile nel caso b, poiché pressoché
RB
RC R E
1
indipendente da (RB è piccola rispetto agli altri due termini a denominatore). Per gli stessi motivi,
il punto di riposo è poco stabile nel caso a.
R 1 gm
Si ha: Av g m RC B
, pertanto l’amplificazione tende a quella tipica di una
RB RC
configurazione ad emettitore comune nel caso a, ovvero tanto più la resistenza RB risulta grande;
infatti, in tal caso si ha: RB 1 g m e RB RC , da cui consegue che: Av g m RC .
Si osserva pertanto che la resistenza RB migliora la stabilità del punto di riposo, ma riduce il valore
dell’amplificazione di tensione].
7) Si dimensionino le resistenze del circuito in figura in modo tale che contemporaneamente uno
dei transistor si trovi in zona attiva, un altro in saturazione e un altro in interdizione.
+VCC = 5 V
R1
RC1
RC2
T1
T3
RB2
T2
R2
RE1
RC3
25
Si consideri che:
a) i tre transistor sono uguali e il guadagno di corrente minimo è min = 80;
b) il partitore d’ingresso R1-R2 lavora “a vuoto” (corrente di base del transistor T1 trascurabile
rispetto alla corrente che scorre nel partitore stesso);
c) il transistor che lavora in saturazione ha un fattore di overdrive pari a 2;
d) le correnti di collettore dei transistor in zona attiva ed in saturazione sono comprese tra 1 e 5 mA.
Dopo aver dimensionato le resistenze, si effettui l’analisi del circuito calcolando i punti di riposo
dei dispositivi attivi, verificando in tal modo la correttezza delle scelte effettuate (prova in itinere
11/06/2009).
[Soluzione:
• T1 in zona attiva: posto IC1 = 2 mA si ottiene RE1 = 835 . Ponendo 0,5 mA = IR1 = IR2 >> IB1, si
ricava R1 = 5,26 k e R2 = 4,74 k.
• T2 in saturazione: posto IB2 = 0,1 mA (<< IE1) si ottiene RB2 = 8,7 k. Con un fattore di overdrive
pari a 2, la corrente di collettore è IC2(sat) = 4 mA da cui si ricava RC2 = 1,2 k.
• T3 risulta sicuramente interdetto perché VBE3 = VCE2 = 0,2 V, insufficiente a polarizzare
direttamente la giunzione BE3, indipendentemente da RC3 che può assumere qualsiasi valore].
8) Un transistor npn al silicio viene realizzato per crescita epitassiale, in modo che i drogaggi delle
zone di emettitore, base e collettore siano indipendenti l’uno dall’altro. Le concentrazioni di
impurità droganti nella zona di emettitore (NDE), di base (NAB) e di collettore (NDC) sono
rispettivamente:
NDE = 1017 cm–3 ;
NAB = 1016 cm–3 ;
NDC = 1015 cm–3 .
La giunzione base-emettitore abbia una sezione di forma quadrata, di lato pari a 100 m, mentre
lo spessore metallurgico della base sia pari a 1,85 m.
Supponendo che il transistor sia mantenuto a temperatura ambiente, si valuti il valore della
resistenza di base RB in assenza di polarizzazione (prova in itinere 11/06/2010).
[Soluzione: RB = 1357 ].
9) Nel circuito di polarizzazione del transistor T in figura, il partitore d’ingresso è ottenuto tramite
un potenziometro da 1 k, in modo tale, cioè, che risulti R1 + R2 = 1 k. Al variare del cursore del
potenziometro – ossia di R1 e R2 – è possibile variare il punto di riposo del transistor (il cui
guadagno ad emettitore comune è pari a
+ VCC = 12 V
100).
Si determini la posizione del cursore del
potenziometro, ossia i valori che devono
RC
assumere R1 e R2, affinché il transistor sia
1 k
condotto rispettivamente:
R1
- in zona di saturazione;
- in zona d’interdizione;
T
k
- in zona attiva, in modo da
R2
massimizzare la dinamica di un
RE
eventuale piccolo segnale applicato in
200
ingresso sulla base (prova in itinere
11/06/2010).
26
[Soluzione: Saturazione: R2 ≥ 233 e R1 ≤ 767 ; Interdizione: R2 ≤ 58 e R1 ≥ 942 ; Zona
attiva (centro): R2 = 142 e R1 = 858 ].
10) Nel circuito in figura, un
+ VCC = 12 V
2,7 k RC
potenziometro da 1 k è utilizzato per
CoC
polarizzare il transistor, in modo tale,
cioè, che risulti R1 + R2 = 1 k. Al
variare del cursore del potenziometro –
R1
ossia di R1 e R2 – è possibile variare il
k
= 100 CoE
R2
punto di riposo del transistor (il cui
Ci
RL
Rs
guadagno ad emettitore comune è pari a
voC
+
v
R
oE
E
100).
vs
330
L’ingresso di tale circuito è costituito
da un generatore di piccoli segnali (a
frequenza tale da poter considerare le capacità presenti nel circuito come dei cortocircuiti), avente
resistenza interna Rs = 50 . Il circuito è provvisto di due uscite: una sul collettore (voC), l’altra
sull’emettitore (voE). Il carico, costituito da una resistenza RL = 2,7 k, può essere collegato
alternativamente ad una delle uscite.
a) Si determini la posizione del cursore del potenziometro, ossia i valori che devono assumere
R1 e R2, affinché il transistor lavori al centro della zona attiva (VCE = VCC /2) e scorra in esso una
corrente di collettore IC = 2 mA.
b) Si calcoli l’amplificazione di tensione voC/vs, relativa all’uscita sul collettore, considerando il
generatore d’ingresso ideale (Rs = 0) e in assenza di carico (RL = ∞), utilizzando lo schema
equivalente dinamico del BJT ed effettuando i calcoli esatti; infine, si mostri che per RE >> 1/gm,
l’amplificazione (in valore assoluto) coincide con il rapporto tra la resistenza di collettore e quella
di emettitore.
c) Si calcoli l’amplificazione di tensione voE/vs, relativa all’uscita sull’emettitore, considerando
il generatore d’ingresso ideale (Rs = 0), sia in assenza di carico (RL = ∞) che in sua presenza (RL =
2,7 k), utilizzando lo schema equivalente dinamico del BJT ed effettuando i calcoli esatti; infine,
si mostri che per RE >> 1/gm, l’amplificazione è pari a 1.
d) Si calcoli l’amplificazione di tensione voC/vs, relativa all’uscita sul collettore, considerando il
generatore d’ingresso reale, cioè avente resistenza interna Rs = 50 , sempre in assenza di carico
(RL = ∞).
e) Si calcoli l’amplificazione di tensione voC/vs, relativa all’uscita sul collettore, considerando il
generatore d’ingresso reale, cioè avente resistenza interna Rs = 50 , quando il carico RL = 2,7 k è
connesso all’uscita.
f) Si dimostri con semplici considerazioni circuitali che l’amplificazione AL in presenza di
RL
carico, si può calcolare come AL A0
(con A0 amplificazione a vuoto, Ro resistenza
Ro RL
d’uscita); si verifichi la correttezza di tale formula nel caso del circuito in esame.
g) Si proponga una soluzione per realizzare l’adattamento di impedenze tra la sorgente, il
circuito e il carico, al fine di rendere indipendente il valore dell’amplificazione globale del circuito
dalla resistenza interna del generatore d’ingresso Rs e dal carico RL (prova in itinere 29/06/2011).
[Soluzione: a. R1 = 887 e R2 = 113 ; b. AvC0 = –8,2; c. AvE0 ≈ 1; d. AvCT0 = –5,5; e. AvCT = –2,75;
f. Per dimostrare l’asserto basta considerare il circuito equivalente dell’uscita dell’amplificatore,
(vale a dire un generatore pilotato di tensione A0·vi in serie alla resistenza d’uscita Ro), connesso
direttamente al carico RL; g. L’adattamento si realizza facilmente inserendo sia a monte, che a valle
dell’amplificatore due stadi a collettore comune].












