Moto esterno

Moto esterno
Argomenti della lezione:
-moto esterno
-sforzi normali e tangenziali
-forza di trascinamento
-area frontale
-coefficiente aerodinamico di penetrazione
-galleria del vento e teoria dei modelli (esempio)
-esercizio 1 : velocità di una goccia di pioggia
-esercizio 2 : spinta del vento sui pali di una linea elettrica
-esercizio 3 : spinta del vento su un edificio
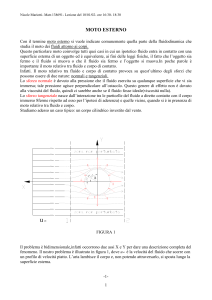
Con il termine moto esterno indichiamo quella parte della fluidodinamica che studia il moto
dei fluidi attorno ai corpi.
Il moto esterno coinvolge tutti quei casi in cui un fluido viene a contatto con la superficie
esterna di un oggetto ed è equivalente, ai fini delle leggi fisiche, il fatto che l’oggetto sia fermo e il
fluido si muova o che il fluido sia fermo e l’oggetto si muova. In sostanza è importante il moto
relativo tra fluido e corpo di contatto.
Infatti, il moto relativo tra fluido e corpo di contatto provoca su quest’ultimo degli sforzi (cioè
forze per unità di superficie) che possono essere di due nature, normale e tangenziale.
Lo sforzo normale è dovuto alla pressione che il fluido esercita su qualunque superficie che vi
sia immersa; tale pressione agisce perpendicolarmente all’ostacolo. Questo genere di effetto non è
dovuto alla viscosità del fluido, perciò interverrebbe anche se il fluido fosse ideale (cioè a viscosità
nulla).
Gli sforzi tangenziali nascono dall’ interazione tra le particelle del fluido a diretto contatto
con il corpo immerso (ferme rispetto ad esso per l’ipotesi di aderenza) e quelle vicine, quando si è
in presenza di moto relativo tra fluido e corpo.
Figura Error! Bookmark not defined.
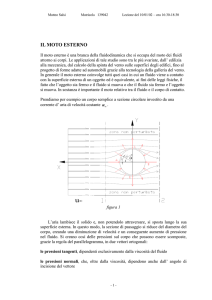
In fig.1 vediamo la sezione frontale del cilindro con
  sforzo normale
  sforzo tangenziale
N
2
che vengono esplicitati come m , cioè come forza su unità di superficie
Figura Error! Bookmark not defined.
La fig. 2 illustra la sezione di un filo cilindrico investito dal fluido. Il fluido lambisce il solido e
non potendolo attraversare si sposta lungo la superficie esterna.
Nel caso di un fluido reale (cioè a viscosità non nulla) si genera tra le particelle del fluido e la
superficie del cilindro un attrito viscoso che provoca la perdita, per scambio termico, di parte
dell’energia cinetica del fluido.
Gli sforzi normali tendono a diminuire procedendo da 0° a 180° in senso orario e l’andamento
della pressione sarà quello illustrato in fig.3. Gli sforzi normali danno luogo ad una forza risultante
F che tende a trascinare il corpo.
Figura Error! Bookmark not defined.
Gli sforzi tangenziali, ossia la tensione esercitata tangenzialmente alla superficie del cilindro,
dovuta all’attrito viscoso del fluido, hanno un andamento illustrato dal grafico in fig.4.
Figura Error! Bookmark not defined.
La forza risultante delle tensioni normali e tangenziali è una forza F applicata nel baricentro del
corpo con direzione e verso concordi a quelli del fluido, detta forza di trascinamento FT la cui
formula è
W2
FT  P  AF    AF 
 CR
2
con
AF  area frontale
  densità del fluido
w 2  u 2  velocità media
CR  coefficiente di penetrazione aerodinamico
(espresso anche come C X oppure come C F )
L’ area frontale è una grandezza caratteristica ed è definita come la proiezione sul muro del
piano d’ombra del corpo ( in fig.5 esempio di area frontale di un camioncino).
Figura Error! Bookmark not defined.
C R è il coefficiente aerodinamico di penetrazione (misura il rapporto fra la velocità di un corpo
e la potenza che gli è necessaria per muoversi a quella velocità).
Ne risulta perciò che una forma è tanto più aerodinamica, quanto più basso è il suo C R .
Per la corretta determinazione numerica del coefficiente C R devono essere noti la forma del
corpo (geometria del corpo) e il numero di Reynolds, la cui formula è
D   u  D
Re  u   


dove
D  lunghezza caratteristica (es.:diametro nel caso di sfera o cilindro)
 = viscosità cinematica del fluido
Il valore di C R si trova su grafici caratteristici delle varie forme geometriche. Nel grafico in
fig.6 è riportato il coefficiente C R in funzione del numero di Reynolds per le forme semplici di
cilindro e sfera.
Figura Error! Bookmark not defined.
Nel caso reale risulta molto complesso calcolare analiticamente il valore  ( ) e (). Per i casi
più complessi, ovvero per casi in cui i solidi non siano delle figure geometriche elementari, è
praticamente impossibile valutare numericamente le grandezze di cui sopra.. Per questi motivi, la
fluidodinamica esterna viene studiata principalmente per via sperimentale, cioè con le cosiddette
gallerie del vento.
Nella galleria del vento un modello dell’oggetto da studiare, mantenuto fisso, viene investito da
una corrente d’aria pari a quella che l’oggetto dovrebbe possedere nel moto reale, spostandosi esso
stesso nell’aria.Si possono così osservare e misurare caratteristiche aerodinamiche, variazioni di
temperatura e di pressione, turbolenze.
Lo studio dei sistemi complessi (per esempio ali di aerei, automobili, radiatori, ecc.)
richiederebbe, specialmente per oggetti di grandi dimensioni, gallerie del vento molto grosse e
quindi molto costose. A questo inconveniente pone rimedio la teoria dei modelli che, come dice la
parola stessa, fa uso di modelli in scala del sistema da studiare. Secondo la teoria dei modelli,
infatti, è possibile studiare la fluidodinamica esterna di un sistema con lunghezza caratteristica L
usando un modello in scala del sistema stesso con lunghezza caratteristica L’<L, i risultati così
ottenuti possono essere riportati sul modello originale tramite numeri puri.
La grandezza caratteristica di un sistema è la dimensione di una particolare zona presa come
riferimento per tutte le altre e scalando questa viene scalato l’intero sistema. Nella studio
fluidodinamica esterna la grandezza presa come riferimento è l’ area frontale (vedi fig.5).
Esempio
Si vuole calcolare la velocità da applicare ad un modello di automobile in galleria del vento in
modo che i risultati ottenuti possano essere riportati correttamente sul modello originale.
Modello scala 1:2
L  4m
u   300 km
h
u ?
L'  2m
'
Re  Re come ipotesi base della teoria dei modelli, che esplicitata diventa
'

u  L
 aria

u ì  L'
 aria
semplificando ottengo
u '  u  
L
Lì
da cui
u '  2u 
u '  600 km
h
600 km h è quindi la velocità da applicare al modello in galleria del vento.
La teoria dei modelli può anche essere utilizzata per calcolare le spinte del vento sugli edifici.
ESERCIZIO 1
Una goccia di pioggia, approssimata con una sferetta di diametro D=1mm , cade liberamente in
aria atmosferica alla temperatura di 20°C. Si vuole calcolare la velocità raggiunta dalla goccia.
F attrito
F peso
Figura Error! Bookmark not defined.
Poiché la goccia è di piccole dimensioni, la sua velocità limitata ci permette di trascurarne le
deformazioni dovute alla pressione dell’aria, che tenderebbero ad appiattirla.
La goccia d’acqua non scende con moto uniformemente accelerato, come si potrebbe pensare,
ma dopo un primo aumento lineare si assesta su un valore asintotico, poiché è soggetta a due forze
in equilibrio fra loro, la forza peso e la forza d’attrito.
In questo caso la forza peso
Fpeso  M  g
M   H 2 O  Vgoccia
dove
e g = accelerazione di gravità
diventa quindi
1
Fpeso   H 2 O    D 3  g
6
dove D è il diametro della goccia (D = 1 mm)
La forza d’attrito è data da
Fattrito  CR   aria 
u2
 AF
2
2
dove u  velocità di caduta e l’area frontale è data da
D 2
AF 
4
Queste due forze all’equilibrio devono essere uguali
1
u 2 D 2
 H 2 O    D3  g  CR   aria   
6
2
4
semplifico e ottengo
1
u2 1
 H 2 O   D1  g  CR   aria   
6
2 4
da cui ricavo
u 
4 Dg  H 2 O


3 CR  aria
Se CR fosse costante u crescerebbe con D .
Ma CR cala all’aumentare di D, quindi la velocità diventa costante.
Questo calcolo ha però un errore, o meglio un’approssimazione, non tiene infatti conto della forza
F
di galleggiamento g (che deriva dal principio di Archimede)
Fg   fluido  V  g
con V  volume
Utilizzo la forza di galleggiamento per ottenere la forza peso netta
Fpeso  Fg  Fpesonetto
La
F pesonetto
è quindi espressa come
Fpesonetto  M  g   H 2 O   aria  V  g
F attrito
F galleggiamento
F peso
Figura Error! Bookmark not defined.
La forza di galleggiamento agisce anche nella goccia d’acqua (fig.8).
La formula per trovare u  diventa quindi
u 
Per trovare CR devo avere il valore di Re

4 Dg  H 2 O   aria


3 CR
 aria

Re 
u  D

Poiché anche Re dipende dalla velocità, devo procedere per tentativi ipotizzando valori di u .
Tentativo 1
Ipotizzo
u*  1m
s
e lo vado a sostituire nella formula precedente
1  0,001
Re 
 58,8
17  10 6
Controllo il valore sul diagramma di Reynolds e trovo
CR  1.7
Sostituisco il valore trovato nell’equazione di u 
4 0.001  9.81 1000  1.2


 2.53 m
s
3
1.7
1.2
Il valore calcolato non concorda con quello di u * che avevamo ipotizzato.
u 
Tentativo 2
Ipotizzo
u *'  2.53 m
s e ottengo
Re 
2.53  0,001
 149
17  10 6
da cui
CR  1
Sostituisco il valore trovato
4 0.001  9.81 1000  1.2


 3.3 m
s
3
1
1.2
'
Il valore calcolato non concorda con quello di u * che avevamo ipotizzato.
u 
Tentativo 3
Riprovo ipotizzando
u *''  3.3 m
s e ottengo
Re 
3.3  0,001
 194
17  10 6
da cui
CR  0.8
e
u 
4 0.001  9.81 1000  1.2


 3.69 m
s
3
0.8
1.2
''
Il risultato ottenuto non concorda con il valore di u  che avevamo ipotizzato. Si deve procedere
ancora per tentativi fino ad arrivare ad un risultato che soddisfi entrambe le equazioni di u  e di Re .
ESERCIZIO 2
Si vuole calcolare il momento flettente alla base del palo in c.a. di una linea elettrica, causata
dall’azione del vento che soffia con velocità di 100 km/h per poterlo dimensionare correttamente.
100 km/h
F (filo)
F (palo)
momento
flettente
Figura Error! Bookmark not defined.
Dati dell’esercizio:
u   100 km  27.77 m
h
s
DFILO  3mm
DPALO  10cm
LFILO  50m
LPALO  10m
M F  F  braccio  momento flettente
Determino la forza del filo
1
FF  C RF  u 2   aria  AFF
2
Calcolo il numero di Reynolds per trovare il coefficiente aerodinamico
u D
27.77  0.003
ReF   FILO 
 4902
 aria
17  10 6
da cui ottengo
C RF  1
Sostituisco il risultato ottenuto nell’equazione iniziale
1
2
FF  1   27.77   1.2  0.003  50  69.4 N
2
C RF
Su superfici piccole le spinte del vento sono irrisorie.
Determino la forza del palo
1
FP  C RP  u 2   aria  AFP
2
Calcolo il numero di Reynolds per trovare il coefficiente aerodinamico
u D
27.77  0.10
ReP   PALO 
 163400
 aria
17  10 6
da cui ottengo
C RP  1.2
Sostituisco il risultato ottenuto nell’equazione della forza
1
2
FP  1.2   27.77   1.2  0.10  10  555 N
2
C RP
F (filo)=69.4N
5m
F (palo)=555N
5m
vento
Figura Error! Bookmark not defined.
In fig.10 il diagramma delle forze (la FPALO è applicata nel baricentro del palo stesso)
Il filo scarica la forza sul palo.
Calcolo il momento alla base del palo
M F  69.4N 10m  555N  5m  3469N  m
Il risultato ottenuto è l’azione a cui il palo in c.a. deve essere dimensionato.
ESERCIZIO 3
Si vuole calcolare la spinta del vento sull’edificio.
1
2
100 km/h
h=30 m
F
b=80 m
Figura Error! Bookmark not defined.
Dati dell’esercizio:
u   100 km  27.77 m
h
s
Sulla parete 1. la pressione agisce sull’intera superficie in maniera uniforme, mentre la velocità è
nulla.
Sulla parete 2. invece non c’è contropressione (la possiamo trascurare), mentre la velocità non è
nulla.
u12
P
u2
P
 1  2  2
2  aria
2  aria
ma per ipotesi
u12
0
2
P2
0
 aria
e semplificando otteniamo
P1
 aria

u 22
2
da cui
27.77  463Pa N 
u2
P1   aria 
 12 
 2
2
2
m 
2
Calcolo la forza F (spinta del vento sull’edificio) in funzione della pressione e dell’area frontale
(area della parete) dall’equazione.
N
F  P1  b  h   463 2  80m  30m  1110000 N
m
Le spinte del vento sono azioni critiche per gli edifici che hanno un grande sviluppo in altezza e
grandi superfici (vengono dimensionati per resistere alle azioni orizzontali).
Un altro caso pericoloso, per le strutture basse, sono le strutture a copertura sferica.
Fy
100 km/h
40 m
Figura Error! Bookmark not defined.
In questo caso la forza di trascinamento è diretta principalmente verso l’alto. Mentre nel caso
precedente ho considerato C x (componente orizzontale di C R ) unitario, in questo secondo esempio
C
il coefficiente y (componente verticale di C R ) non è trascurabile.
Considero il caso più clamoroso
C y  10
Utilizzo questo valore per trovare
Cy
27.77   1600  7403000 N
u2
 AF  10  1.2 
2
2
Il valore ottenuto è molto più grande del peso della struttura, che va in crisi facilmente.
Per il calcolo delle azioni del vento esistono delle norme UNI che indicano i fattori di sicurezza
anche per le strutture geometriche più complicate.
Fy  C y   aria 
2