Matteo Salsi
Lezione del 10/01/02 – ora 16:30-18:30
Matricola 139042
IL MOTO ESTERNO
Il moto esterno è una branca della fluidodinamica che si occupa del moto dei fluidi
attorno ai corpi. Le applicazioni di tale studio sono tra le più svariate, dall’ edilizia
alla meccanica, dal calcolo della spinta del vento sulle superfici degli edifici, fino al
progetto di forme adatte ad automobili grazie alla tecnologia della galleria del vento.
In generale il moto esterno coinvolge tutti quei casi in cui un fluido viene a contatto
con la superficie esterna di un oggetto ed è equivalente, ai fini delle leggi fisiche, il
fatto che l’oggetto sia fermo e il fluido si muova o che il fluido sia fermo e l’oggetto
si muova. In sostanza è importante il moto relativo tra il fluido e il corpo di contatto.
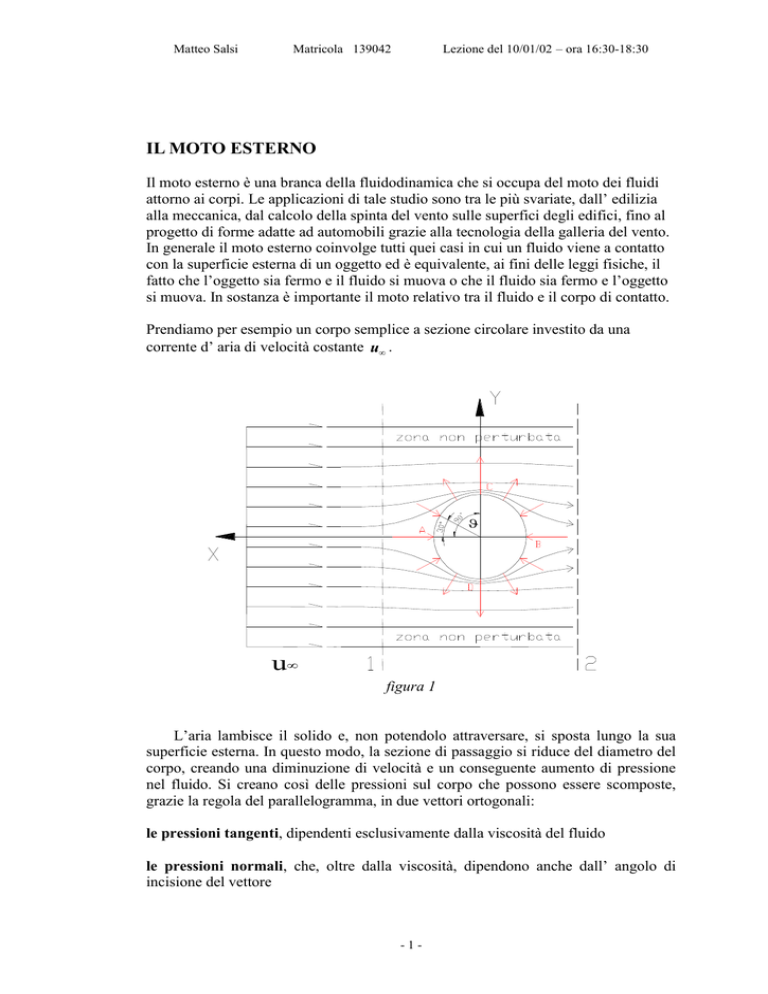
Prendiamo per esempio un corpo semplice a sezione circolare investito da una
corrente d’ aria di velocità costante u .
u
figura 1
L’aria lambisce il solido e, non potendolo attraversare, si sposta lungo la sua
superficie esterna. In questo modo, la sezione di passaggio si riduce del diametro del
corpo, creando una diminuzione di velocità e un conseguente aumento di pressione
nel fluido. Si creano così delle pressioni sul corpo che possono essere scomposte,
grazie la regola del parallelogramma, in due vettori ortogonali:
le pressioni tangenti, dipendenti esclusivamente dalla viscosità del fluido
le pressioni normali, che, oltre dalla viscosità, dipendono anche dall’ angolo di
incisione del vettore
-1-
Lezione del 10/01/02 – ora 16:30-18:30
Zoommando
in una parte qualsiasi del nostro oggetto avremmo una
schematizzazione simile alla seguente.
N
tensione normale
N
T tensione tangenziale
T
figura 2
Nei fluidi ideali, di viscosità pari a zero, l’ unica tensione da considerare è quella
normale e rimane, come unico parametro influente, l’ angolo di incisione . Nei punti
A e B dove il calo di velocità sarà più improvviso, la pressione sarà massima. Tali
punti sono chiamati punti di ristagno . Al contrario, nei punti C e D, dove il fluido ha
velocità massima, si avrà la pressione minima. Si può custuire un grafico dell’
andamento delle pressioni in rapporto agli angoli , dove vale 0° in A e 180° in B.
Fluido ideale
P
r
e
s
s
i
o
n
e
pr
ps
0°
90°
180°
Angolo
Grafico 1
Il grafico 1 mostra come nei fluidi reali la pressione nei punti di ristagno a 0° e a
180° sia identica. In realtà tali tensioni non sono proprio identiche in quanto si
-2-
Lezione del 10/01/02 – ora 16:30-18:30
verifica in B una leggera perdita di tensione. Il grafico dei fluidi reali sarà così
diverso.
Fluido ideale
P
r
e
s
s
i
o
n
e
Fluido reale
pr
ps
0°
180°
90
°
Angolo
Grafico 2
Nei diagrammi si nota anche che nei punti C e D, dove è uguale a 90°, le
pressioni assumono valori negativi. Tale fenomeno ha, sul corpo, l’ effetto di creare
tensioni che tendono a deformare l’ oggetto nella direzione perpendicolare al flusso.
corpo deformato
dalle pressioni
corpo non ancora
investito dal fluido
figura 3
Le pressioni positive sono, comunque, sempre maggiori delle negative e la loro
risultante totale è una forza di trascinamento che segue l’ andamento del flusso.
-3-
Lezione del 10/01/02 – ora 16:30-18:30
Tale forza dipende dalla viscosità, dalla velocità e dalla densità del fluido, e
calcolarne l’ intensità è lo scopo della fluido dinamica. La formula è la seguente:
FT P AF AF
W2
CR
2
dove
FT
ΔP
AF
ρ
W
CR
è la forza di trascinamento
è la variazione di pressione
è l’ area frontale
è la densità del fluido
è la velocità del flusso ed è uguale a u
è il coefficiente di penetrazione
Nella formula vengono introdotti concetti nuovi, quali l’ area frontale e il
coefficiente CR.
L’ area frontale non è altro che la proiezione del corpo su un piano di riferimento
perpendicolare alla direzione del flusso. L’ area che si determina è la nostra area di
riferimento da inserire nella formula.
figura 4
L’ area frontale rappresenta il fattore di proporzione tra la pressione e la forza di
trascinamento.
Il coefficiente di penetrazione CR (detto anche CF o CX) rappresenta il rapporto tra la
velocità del corpo e la potenza necessaria per muoversi a quella velocità. Per
-4-
Lezione del 10/01/02 – ora 16:30-18:30
calcolarne il giusto valore sono necessarie particolari grafici che relazionano CR al
numero di Reynolds. Per trovare tale coefficiente serve la seguente formula:
RE
u D
u D
dove
RE è il numero di Reynolds
è la viscosità cinematica del fluido
Trovato il numero di Reynolds è possibile ricavare il coefficiente di penetrazione
dalla corrispondente tabella.
Grafico 3
-5-
Lezione del 10/01/02 – ora 16:30-18:30
Nelle forme complesse prive di un diametro geometrico si ricava un diametro
equivalente utilizzabile nella formula.
DEQ
4 V
S
Tale formula è, per esempio, utilizzabile nella progettazione di profili alari dove il
rapporto tra CX e Cy definisce l’ angolo di planata.
CX, Cy
Fy
Cy
FX
CX
RE
profilo di un' ala
grafico di Reynolds corrispondente
figura 5
Per il calcolo aereodinamico di strutture complesse sono comunque necessarie
verifiche pratiche che permettano di studiare la reazione reale dell’ oggetto al flusso
d’ aria. Per questo motivo vengono costruite le cosidette gallerie del vento, strutture
che permettono la creazione di “venti” artificiale attraverso l’ uso di enormi ventole e
filtri stabilizzatori di flusso. Utilizzando la teoria dei modelli le dimensioni di tali
attrezzature possono essere ridotte (con un conseguente risparmio economico) e i test
aereodinamici possono essere effettuati non più sull’ oggetto reale ma, bensì, su dei
modelli in scala ridotta. L’ unico inconveniente di tale teoria è il fatto che la velocità
del fluido deve, per ottenere risultati simili alla realtà, aumentare in modo
prorzionale alla diminuzione di dimensione dell’ oggetto. Se per esempio vogliamo
verificare il profilo di un automobile utilizzando un modello in scala 1:2 la velocità
dell’ aria nella galleria del vento dovrà essere doppia rispetto a quella reale.
ESEMPIO
Ipotizziamo i seguenti dati:
LV = 4 m
LM = 2 m
u = 300 km/h
(lunghezza dell’ automobile vera)
(lunghezza del modello)
(velocità del flusso d’ aria nella realtà)
Calcolare la velocità che l’ aria deve avere nella galleria del vento.
-6-
Lezione del 10/01/02 – ora 16:30-18:30
Sapendo che i numeri di Reynolds del modello e dell’ automobile sono identici si
ricava facilmente la velocità incognita.
REV = REM
u
LV
ARIA
u X u
uX
LM
ARIA
LV
300 2 600 Km/h
LM
Ai fini del nostro studio le applicazioni pratiche di tali teorie sono ben diverse in
quanto il nostro interesse è indirizzato soprattutto alle pressioni del vento su gli
edifici e sulle strutture in generale. Vediamo ora qualche esempio reale.
ESERCIZIO 1
Calcolare la velocità con cui cadono le goccie di pioggia, ipotizzando che esse siano
perfettamente sferice (in realtà le goccie si deformano per l’ attrito dell’ aria in modo
del tutto simile alla figura 3). A livello teorico la nosta sfera dovrebbe continuare ad
accellerare all’ infinito, secondo la legge del moto uniformemente accellerato, ma la
presenza dell’ aria stabilizza la velocità dopo un centinaio di metri di caduta.
v
vmax
T
Incremento di velocità nel tempo
Grafico 4
-7-
Lezione del 10/01/02 – ora 16:30-18:30
Il momento preciso in cui il corpo inizia a muoversi di moto rettilineo uniforme è
quando la Forza peso diventa uguale alla Forza d’ attrito. Sfruttando questo
fenomeno possiamo trovare facilmente la velocità di caduta della goccia d’ acqua.
FA
D
FP
figura 6
Ipotizzando il diametro della goccia uguale a 1 mm possiamo scrivere le seguenti
equazioni della forza peso e della forza d’ attrito.
1
F p M g H 2O V g H 2O D 3 g
6
FA C R ARIA
u2
u2
D2
AF C R ARIA
2
2
4
Uguagliando i secondi membri delle formule si ricava la u .
H O
2
u2
1
D2
3
D g C R ARIA
6
u
4
u
4 D g H 2O
3
CR
ARIA
-8-
Lezione del 10/01/02 – ora 16:30-18:30
Proviamo ora a risolvere un problema analogo. Cerchiamo di calcolare la velocità di
caduta di un masso in mare considerando in più la forza di galleggiamento di
Archimede.
Fg + F A
FP
figura 7
Con la forza di galleggiamento posso ricavare la forza peso netta e la formula
generale della velocità di caduta di un oggetto in un fluido.
Fg H 2O V g
FPn FP Fg ( SASSO H 2O ) V g
u
4 D g SASSO H 2O
3
CR
H 2O
Giunti a questo punto sorge un altro problema: per trovare CR è necessario il numero
di Reynolds che dipende dalla velocità u che vogliamo determinare. Infatti
RE
u D
L’ unico modo per uscire da questo vicolo cieco è quello di procedere a tentativi
ricavando con valori casuali il numero di Reynolds e sperando di trovare la
medesima velocità nella formula di u .
-9-
Lezione del 10/01/02 – ora 16:30-18:30
Tentiamo, per esmpio, di trovare la velocità della goccia di pioggia considerando in
più la forza di galleggiamento esercitata dall’ aria. Iniziamo a inserire dei valori
casuali della velocità.
TENTATIVO 1
u1 1 m/s
RE 1
u
1 0,001
58,8 C R 1,7
17 10 6
4 0,001 9,81 1000 1,2
2,53 m/s
3
1,7
1,2
Le velocità u1 e u sono diverse. Proviamo ora inserendo una velocità uguale a
2,53 m/s.
TENTATIVO 2
u2 2,53 m/s
RE 2
2,53 0,001
149 C R 1
17 10 6
u
4 0,001 9,81 1000 1,2
3,30 m/s
3
1
1,2
Le velocità non coincidono ancora. Tentiamo ancora con la velocità pari a 3,30 m/s.
TENTATIVO 3
u3 3,30 m/s
RE 2
3,30 0,001
194 C R 0,8
17 10 6
- 10 -
Lezione del 10/01/02 – ora 16:30-18:30
u
4 0,001 9,81 1000 1,2
3,69 m/s
3
0,8
1,2
Il risultato ottenuto, anche se non ancora preciso, si è avvicinato notevolmente alla
soluzione. Continuando con questo procedimento, con ancora un paio di tentativi,
otterremmo il valore esatto della velocità di caduta della goccia di pioggia nell’
atmosfera.
ESERCIZIO 2
Calcolare il momento flettente che si crea alla base di un palo della luce sotto la
spinta di un vento di 100 Km/h. Il risultato è necessario per il giusto
dimensionamento del palo.
VV
FF
FP
FP
MP
MP
figura 8
I dati sono i seguenti:
u 100 km 27.77 m
h
s
DFILO 3mm
DPALO 10cm
LFILO 50m
LPALO 10m
- 11 -
Lezione del 10/01/02 – ora 16:30-18:30
Iniziamo l’ esercizio calcolando i numeri di Reynolds e l’ intensità delle forze
esercitate sul palo e sul filo.
ReF
u DFILO
aria
27.77 0.003
4902
17 10 6
C RF 1
1
2
FF 1 27.77 1.2 0.003 50 69.4 N
2
ReP
u DPALO
aria
27.77 0.10
163400
17 10 6
C RP 1.2
1
2
FP 1.2 27.77 1.2 0.10 10 555 N
2
Trovati questi risultati possiamo schematizzare il problema e trovare facilmente il
momento incognito.
FF
FP
figura 9
Il momento alla base del palo sarà uguale a:
M F 69.4N 10m 555N 5m 3469N m
- 12 -
Lezione del 10/01/02 – ora 16:30-18:30
Da questo esempio si può vedere quanto conti nella spinta del vento l’ area frontale.
Il filo, infatti, lungo ben 50 m subisce una forza di appena 7 kg proprio a causa della
sua sezione ridotta. Vediamo ora quanto enorme può essere questa forza su un
palazzo di notevoli dimensioni.
ESERCIZIO 3
Trovare la forza esercitata dal vento che soffia a 100 km/h su un palazzo alto 30 m e
lungo 80.
F
figura 10
I dati sono i seguenti:
VV = 100 km/h = 27,77 m/s
HPALAZZO = 30 m
BPALAZZO = 80 m
( velocità del vento)
( altezza del palazzo )
( lunghezza del palazzo )
Dato che siamo nel campo dell’ edilizia e che dobbiamo avere un buon margine di
sicurezza, ipotizziamo che a monte dell’ edificio (a sinistra nel disegno) vi sia solo
pressione di ristagno, mentre a valle nessuna contropressione. La formula si può così
semplificare:
u12
P1
u 22
P
2
2 aria
2 aria
P1
aria
- 13 -
u 22
2
Lezione del 10/01/02 – ora 16:30-18:30
Ora si può ricavare la pressione del vento e, moltiplicando per l’ area frontale dell’
edificio, si trova la forza esercitata sul palazzo.
P1 aria
27.77 463Pa N
u2
12
2
2
2
m
2
F P1 b h 463
N
80m 30m 1110000 N
m2
Come si può vedere la forza è notevole ed è per questo motivo che i grattacieli
reagiscono meglio alle sollecitazioni orizzontali che a quelle verticali. Tutto ciò
comporta un sovraddimensionamento delle strutture e un conseguente aumento delle
spese. Oltre all’ area frontale è, comunque, importante tener conto della forma forma
stessa dell’ edificio. Nelle costruzioni, per esempio, coperte con delle volte a botte
può succedere che le pressioni causate dal vento generino una risultante diretta verso
l’ alto. Questo è molto pericoloso perchè obbliga la struttura a lavorare al contrario
con carichi dieci volte più grandi del peso del tetto. Facciamo un esempio:
F
y
figura 11
Consideriamo un caso estremo dove il C y è uguale a 10. Per tutti gli altri dati
utilizzeremo quelli dell’ esercizio precedente.
Fy C y aria
27.77 1600 7403000 N
u2
AF 10 1.2
2
2
2
Per progettare in sicurezza anche con questi carichi esitono, comunque, particolari
norme U.N.I che forniscono, anche delle forme più complesse, gli specifici
coefficenti di portanza aereodinamica.
- 14 -
Lezione del 10/01/02 – ora 16:30-18:30
- 15 -
Lezione del 10/01/02 – ora 16:30-18:30
- 16 -