Generalità sulle macchine rotanti

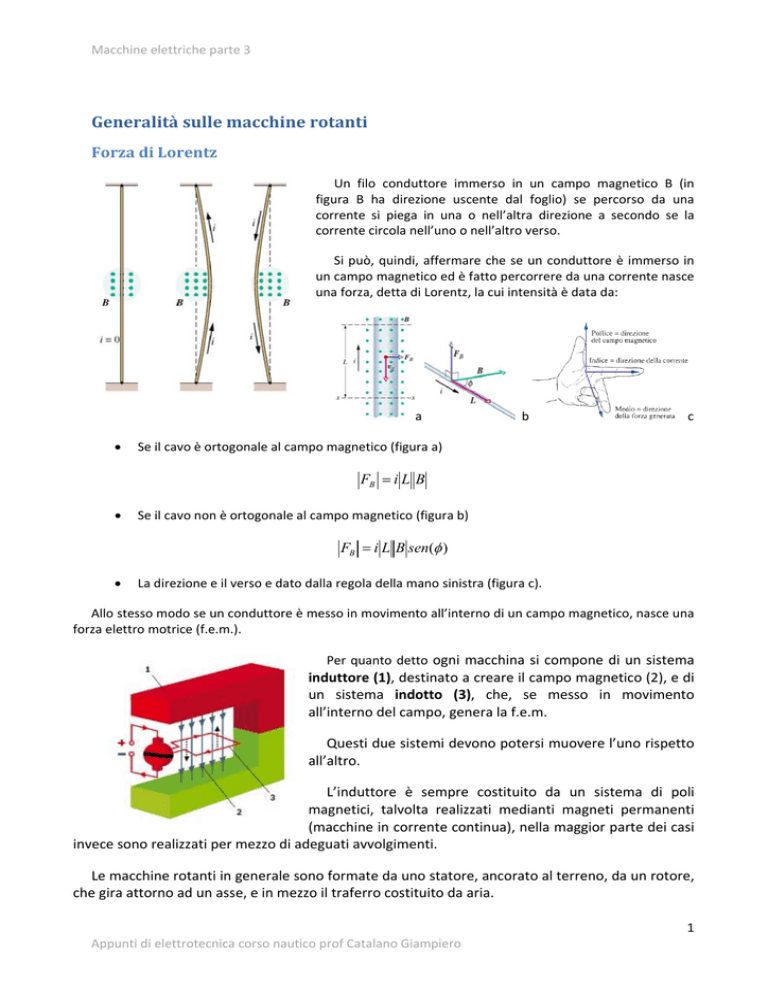
Macchine elettriche parte 3 Generalità sulle macchine rotanti Forza di Lorentz Un filo conduttore immerso in un campo magnetico B (in figura B ha direzione uscente dal foglio) se percorso da una corrente si piega in una o nell’altra direzione a secondo se la corrente circola nell’uno o nell’altro verso. Si può, quindi, affermare che se un conduttore è immerso in un campo magnetico ed è fatto percorrere da una corrente nasce una forza, detta di Lorentz, la cui intensità è data da: a

b
c Se il cavo è ortogonale al campo magnetico (figura a) FB  i L B 
Se il cavo non è ortogonale al campo magnetico (figura b) FB  i L B sen( ) 
La direzione e il verso e dato dalla regola della mano sinistra (figura c). Allo stesso modo se un conduttore è messo in movimento all’interno di un campo magnetico, nasce una forza elettro motrice (f.e.m.). Per quanto detto ogni macchina si compone di un sistema induttore (1), destinato a creare il campo magnetico (2), e di un sistema indotto (3), che, se messo in movimento all’interno del campo, genera la f.e.m. Questi due sistemi devono potersi muovere l’uno rispetto all’altro. L’induttore è sempre costituito da un sistema di poli magnetici, talvolta realizzati medianti magneti permanenti (macchine in corrente continua), nella maggior parte dei casi invece sono realizzati per mezzo di adeguati avvolgimenti. Le macchine rotanti in generale sono formate da uno statore, ancorato al terreno, da un rotore, che gira attorno ad un asse, e in mezzo il traferro costituito da aria. 1 Appunti di elettrotecnica corso nautico prof Catalano Giampiero Macchine elettriche parte 3 A questo tipo di macchine appartengono, come detto più volte, i generatori e i motori. Polo magnetico Consideriamo il sistema di figura, esso è costituito da una bobina formata da N spire, percorsi da una corrente continua “i”. In queste condizioni la forza magneto‐motrice (f.m.m.) generata dagli avvolgimenti è data dalla relazione f .m.m  Ni Supponiamo adesso di alimentare il rotore con una tensione sinusoidale, allora anche la corrente è sinusoidale e di conseguenza anche la f.m.m. sarà sinusoidale è sarà data dalla relazione: f .m.m  N I sen(t   ) In pratica il vettore f.m.m. è pulsante e inverte la sua polarità ogni mezzo periodo. Diremo polo nord l’effetto che provoca la semionda positiva e polo sud l’effetto che provoca la semionda negativa. Angolo elettrico ed angolo meccanico Si è visto che per costruire una macchina elettrica rotante, occorre generare un campo magnetico, e al suo interno bisogna mettere in rotazione una spira di materiale conduttore. Allo stesso risultato si arriva se il sistema induttore è posto sul rotore e il sistema indotto e posto sullo statore come rappresentato in figura (due poli). Supponiamo di alimentare gli avvolgimenti di statore con una tensione continua, come detto si genera una f.m.m. anch’essa costante. Supponiamo adesso di mettere in rotazione il rotore (con velocità costante); una spira posta sullo statore sarebbe investita dal campo magnetico e lo vedrebbe variare passando da polo nord a sud con la stessa velocità con cui ruota l’avvolgimento e la tensione che essa genererà sarà una grandezza variabile, periodica, sinusoidale e con frequenza pari a quella di rotore. Supponiamo adesso di aggiungere altri due poli, in questo caso quando il rotore avrà fatto un giro completo, una spira posta sullo statore vedrebbe passare due volte il polo nord e due volte il polo sud nella sequenza N‐S‐N‐S, f.e.m. generata avrà frequenza doppia rispetto a quella di rotore. Definiremo, allora, angolo meccanico m quello con cui ruota il rotore ed angolo elettrico e quello con cui ruota la grandezza elettrica associata alla rotazione del polo magnetico. 2 Appunti di elettrotecnica corso nautico prof Catalano Giampiero Macchine elettriche parte 3 I due angoli sono legati dalla relazione: e  p m Dove p rappresenta il numero di coppie polari. Infatti, nel primo caso p = 1 (una sola coppia polare) e l’angolo elettrico coincideva con quello meccanico; nel secondo caso p = 2 (due coppie polari) e l’angolo elettrico è il doppio di quello meccanico. Campo magnetico rotante Ci chiediamo adesso è possibile generare un campo magnetico che, anche se le bobine sono ferme, è in grado di girare? La risposta si deve al torinese Galileo Ferraris. Supponiamo di disporre in una stanza tre avvolgimenti identici a 120° meccanici tra loro. Supponiamo di alimentare questi tra avvolgimenti con tre tensioni simmetriche; f.m.m.1
12
0°
0°
12
E1  Esen(t )
E2  Esen(t  120) f.m.m.2
f.m.m.3
120°
E3  Esen(t  120)
essi genereranno tre f.m.m. di uguale intensità e sfasate fra loro di 120° elettrici. f .m.m.1  NIsen(t )
f .m.m.2  NIsen(t  120) f .m.m.3  NIsen(t  120)
Nello spazio l’azione di queste tre f.m.m. sarà data dalla risultante di tre vettori che le rappresentano. Vediamo come varia questa f.m.m. al variare del tempo: per t1 = 0 si ha t = 0 allora: f .m.m.1  Nisen(0)  0
f .m.m.2  Nisen(120)  
f .m.m.3  Nisen(120) 
-f.m.m.2
f.m.m.tot
f.m.m.2
f.m.m.3
3
NI 2
3
NI
2
Applicando la regola del parallelogramma si ottiene la f.m.m.totale, il cui modulo vale 1.5NI ed è diretta nello spazio a 180°. Per t2 = /6 (/6 = 30°) si ha: 3 Appunti di elettrotecnica corso nautico prof Catalano Giampiero Macchin
ne elettriche parte 3 f .m.m.1  Nisen
N
(30)  0.5 NI
f .m.m.2  Nisen
N
(90)   NI f .m.m.3  Nisen
N
(150)  0.5 NI
f.m.m.12
f.m.m
m.tot
150°°
f.m.m.2
f.m
m.m.1
Applicando la regola del A
d parallelo
ogramma si ottiene laa f.m.m
m.totale, il cui modulo vaale, ancora, 1.5NI ed è diretta d
nello
o spazzio a 150°. f.m.m
m.3
A
Analogament
te se consid
derano gli isstanti t3 = /3 
(/6 = =
60°),, t4 = /2 ((/2 = 90°), etc. si trova che la f.m.m
m.totale è unaa gran
ndezza che ru
uota con freq
quenza pari a quella dellle grandezzee eletttriche t, ed
d ha ampiezzza pari a 1.5
5NI. come rappresentato
o in figura. t3
t4
t2
t1=0
=
Si è creeato, quindi, un campo magnetico rotante con
n frequenza pari alle grandezze ch
he lo hanno
o generato (la terna di corrente c
equ
uilibrata) ed ampiezza pari p a 1.5 vo
ote l’ampiezzza delle sin
ngole f.m.m.. generate. Macch
hina asin
ncrona triifase La macch
hina asincro
ona è formaata da uno statore chee c
contiene gli a
avvolgimentii induttori, p
posti a 120° ffra loro, e daa u rotore, rappresenttate l’indottto, costituito da un
un n a
avvolgimento
o chiuso in co
ortocircuito.. Alimentan
ndo i tre avvvolgimenti d
di statore con una ternaa ssimmetrica d
di tensioni, sii genera il caampo magne
etico rotantee c
con velocità 
0, pari alla ffrequenza dii rete. L’avvolgim
mento di roto
ore vedrà, allmeno nella fase iniziale,, u campo magnetico un m
variabile a frequenza 0. In esso, perr e
effetto dellaa legge di Lenz, L
nasce una corrente (perchéé c
chiuso in cortocircuito) che metteràà in rotazione il rotoree (forza di Lorentz) il quale per opporsi alla caussa che lo haa g
generato inse
eguirà il cam
mpo magneticco in modo d
da annullaree laa variazione
e. Quando il rotore raaggiunge la velocità dii sincronismo
o, cioè quella con cui ruota il campo
o magnetico, non vedrà più variare il campo, infatti, campo
o 4
4 Appunti di elettroteccnica corso n
nautico prof Catalano Giaampiero Macchine elettriche parte 3 magnetico e rotore si muovono alla stessa velocità, allora rallenta; Appena rallenta rivede variare il campo magnetico e, quindi, riaccelera. In conclusione affinché il rotore possa rimanere in rotazione, occorre che la velocità 0 del campo magnetico sia sempre maggiore (di poco) della velocità di rotore r. ecco perché si chiama macchina asincrona, poiché per funzionare occorre che non ci sia sincronismo tra campo magnetico e velocità di rotazione del rotore. Le correnti indotte allo statore (le correnti che nascono a causa della variazione del flusso), saranno correnti di piccola intensità, sinusoidali e con frequenza pari alla velocità relativa tra grandezze di rotore e quelle di statore: rel = 0 ‐ r La velocità con cui ruota il campo magnetico espressa in rad/s vale: 0 
2f 0
(p  numero di coppie polari) p
Essa può essere espressa anche in giri al minuto (rpm) n0 
60 f 0
p
Allo stesso modo: La velocità con cui ruotano le grandezze di statore espressa in rad/s vale:  rel 
2f r
(p  numero di coppie polari) p
Essa può essere espressa anche in giri al minuto (rpm) nrel 
60 f r
p
Un parametro utile per valutare la condizione di sincronismo e lo scorrimento, definito come il rapporto tra la velocità relativa rel, e quella di sincronismo 0. s
 rel  0  r n rel n 0 n r



0
0
n0
n0
Esso è spesso indicato in percentuale. s %  100
n
n n
 rel
 
 100 0 r  100 rel  100 0 r n0
n0
0
0
Vediamo quali informazioni possiamo ricavare dallo scorrimento appena definito. 5 Appunti di elettrotecnica corso nautico prof Catalano Giampiero Macchine elettriche parte 3 Lo scorrimento varia tra zero e uno, infatti: 

Quando il rotore è fermo r = 0 allora s = 1 (100%); Quando il rotore gira liberamente (senza carico) r  0 pertanto s  0 . Osserviamo che s non può essere uguale a zero proprio per come funziona la macchina. Da quanto detto si nota che all’avviamento, essendo lo scorrimento pari a uno, la corrente assorbita dalla macchina risulta 7 – 8 volte la corrente nominale. Detta corrente prende il nome di corrente di spunto e bisogna tenerne conto quando si progettano le protezioni per i motori. Vediamo adesso come esprimere le grandezze di rotore con quelle di statore.   rel
 rel  s0
s  
p0


0
 fr  s
 sf 0 

p
2
  2f r
 f r  2 rel
 rel
p
In pratica la frequenza di rotore si può ricavare dalla frequenza di statore attraverso lo scorrimento. Circuito equivalente di una macchina asincrona. Se si osserva bene, la macchina asincrona, è come un trasformatore con secondario che ruota e chiuso in cortocircuito, per cui il suo circuito equivalente (riferito ad una sola fase) è come quello del trasformatore in cortocircuito. Osserviamo che l’impedenza di dispersione al secondario lavora a frequenza di rotore che, come sappiamo, è diversa da quella di statore. Risulta conveniente (per usare i fasori) riportare tutto alla frequenza di statore. Scriviamo LKT al secondario: R

E2  R2  jX R I 2  R2  jLd 2 I 2  R2  j 2f r Ld 2 I 2  R2  j 2sf o Ld 2 I 2  s 2  j 2f o Ld 2  I 2  s

Se indichiamo E20 = E2/s, e ricordando che Xd2 = 2f0Ld2, equazione sopra si scrive: R

E02   2  jX d 2  I 2  s

Allora il circuito equivalente diventa: 6 Appunti di elettrotecnica corso nautico prof Catalano Giampiero Macchine elettriche parte 3 La potenza dissipata dalla resistenza R2/s rappresenta la potenza trasferita dallo statore al rotore, ed è denomina la potenza trasmessa P12. Il circuito equivalente appena trovato non ci dice nulla sul carico. Per mettere in evidenza anche la potenza dissipata sul carico occorre applicare uno stratagemma matematico, infatti: R2
R
1 
1 s 
 R2  R2  2  R2    1 R2  R2  
 R2 s
s
s 
 s 
Allora il circuito equivalente diventa: Le perdite nella macchina asincrona possono essere così schematizzate. 7 Appunti di elettrotecnica corso nautico prof Catalano Giampiero