J - Hoepli

2
Analisi delle reti
Esercitazioni aggiuntive
Esercizio 2.1
Calcolare la tensione ai capi A e B del seguente circuito, applicando il teorema di Millman:
A
+
E
R2
I
I1
R1
B
E = 10 [v]
I = 1 [A]
I1 = 1 [A]
R1 = 10 [Ω]
R2 = 20 [Ω]
Esaminando il circuito si osserva, da sinistra verso destra, che:
– il primo ramo, tra i punti A e B, è costituito soltanto da un generatore di corrente;
– il secondo contiene un generatore di tensione ideale con una resistenza in serie;
– il terzo consiste soltanto di una resistenza;
– il quarto è costituito da un generatore di corrente.
Per determinare la tensione VAB occorre quindi adoperare la seguente formula:
E
10
+I
R1 1 1 + 10 + 1
=
=
= 20 [v]
1
1
1
1
+
+
R1 R2
10 20
I+
VAB
Si osservi come, nota VAB, sia necessario usare altre relazioni per risolvere la rete.
Si osservi ancora che per determinare rapidamente la tensione VAB sarebbe bastato trasformare la
serie E – R1 in un generatore reale di corrente e poi calcolare il parallelo sia dei generatori di corrente
sia delle resistenze, ottenendo quindi una rete a una sola maglia.
2
Analisi delle reti
Esercizio 2.2
Determinare le tensioni e le correnti in tutti i rami della seguente rete:
R3
+
I
R1
R2
E
R4
I = 1 [A]
E = 5 [v]
R1 = 10 [Ω]
R2 = 10 [Ω]
R3 = 8 [Ω]
R4 = 2 [Ω]
Si valuti, per prima cosa, la serie R3 – R4.
Rs = R3 + R4 = 10 [Ω]
Si effettui poi la trasformazione Thevenin-Norton per il generatore ideale E con in serie la resistenza Rs :
+
E
Rs
I
Rs
in cui I ' =
E
= 0.5 [A].
Rs
Si ottiene così il seguente circuito:
I
IR1
I1
IR2
IRs
R1
R2
Rs
I’
3
esercitazioni
che si trasforma in:
Ip
'
con I p = I + I = 1.5 [A] ed
Rp
1
1
1
1
=
+
+
= 0.3 [S]; R p ≅ 3.3 [W].
R p R1 R2 Rs
La tensione su R p è:
VR = I p R p = 4.9 [v]
p
Inoltre VI = VR = VR = VR = VR , quindi:
1
2
s
p
IR =
1
VR
= 0.49 [A]
1
R1
poichè R2 = R1 è:
I R = I R = 0.49 [A]
2
1
Riferendosi, ora, al circuito iniziale si osserva che:
I R = I R = I E = I1
I1 + I R + I R − I = 0
I1 = I − I R − I R = 0.02 [A]
3
4
1
1
2
2
Quindi:
VR = I1 R3 = 0.16 [v]
3
VR = I1 R4 = 0.04 [v]
4
VR + E + VR = 5.2 ≠ VR = 4.9
3
4
p
Questo non è accettabile perchè la differenza di potenziale tra due punti deve risultare la stessa
qualunque siano il percorso e il modo con cui venga calcolata. Questa discrepanza deriva dall’approssimazione alla prima cifra decimale su Rp.
Si rifacciano i calcoli calcolando Rp con 3 cifre decimali.
4
Analisi delle reti
Esercizio 2.3
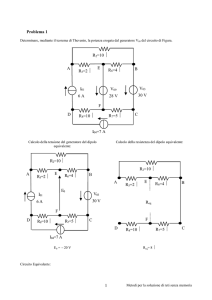
Applicare il teorema di Thevenin alla rete lineare rispetto ai morsetti A e B.
R3
A
R1
R4
+
R2
I
E
B
E = 20 [v]
I = 3 [A]
R1 = 5 [Ω]
R2 = 4 [Ω]
R3 = 8 [Ω]
R4 = 16 [Ω]
Calcolo della resistenza della rete equivalente di Thevenin, che è quella vista dai morsetti A e B
cortocircuitando il generatore di tensione indipendente E e aprendo il generatore di corrente indipendente I.
Definendo R’eq come il parallelo di R2, R3 ed R4 si ha:
1
'
Req
=
1
1
1
+
+
= 0.4375 [S],
R2 R3 R4
e quindi:
'
Req
= 2.2857 [W]
La resistenza della rete equivalente di Thevenin vale quindi:
'
Req = R1 + Req
= 7.2857 [W]
Calcolo della tensione del generatore Veq della rete equivalente di Thevenin.
Definendo RP come il parallelo tra R3 ed R4 si ha:
RP =
R3 R4
= 5.3333 [W]
R3 + R4
La rete, con la sostituzione di RP al parallelo tra R3 ed R4, diventa:
5
esercitazioni
Rp
R1
A
+
R2
E
I
B
Effettuando la trasformazione Norton-Thevenin del generatore di corrente I:
R2
R2
I
+
E¢
definendo
E ' = IR2 = 12 [v]
si ottiene la rete:
A
R1
Rp
A’
I1
VR2
R2
VRp
VA’B
+
E’
B
Si può scrivere:
E ' − VR − VR − E = 0
2
P
Poichè:
VR = I1 R2
2
VR = I1 RP
P
si ottiene:
E ' − I1 R2 − I1 R p − E = 0
+
E
6
Analisi delle reti
Da quest’ultima si calcola allora:
I1 =
E' − E
= −0.8571 [A]
R2 + R p
Si osservi che è anche:
VA ' B + VR − E ' = 0
2
Quindi:
VA ' B = E ' − VR = E ' − I1 R2 = 15.4284 [v]
2
Allora:
Veq = VAB = VA ' B = 15.4284 [v]
Esercizio 2.4
Data la rete riportata in figura si determini la tensione ai capi del generatore di corrente I.
R1
I1
J1
R2
+
E
R3
J2
I
VI
+
V1
J3
E = 10 [v]
V1 = hI1 [v]
I = 1 [A]
R1 = 60 [Ω]
R2 = 30 [Ω]
R3 = 20 [Ω]
h = 2 [Ω]
La rete è costituita da 3 maglie indipendenti e contiene 3 nodi indipendenti; pertanto ai fini della sua
risoluzione risulta indifferente utilizzare o il metodo delle correnti di maglia o quello dei potenziali di
nodo. Si consideri, anche, che il potenziale del nodo a cui sono collegati sia il generatore di corrente
I che il generatore pilotato di tensione V1 non è noto, dato che quest’ultimo dipende dalla corrente
su R1.
Si scelga, inizialmente, di determinare la grandezza cercata usando il metodo delle correnti di
maglia.
Si scelgano arbitrariamente le correnti di maglia J1, J2, J3; si scriva, poi, il sistema risolvente,
ricordando di esprimere tramite le correnti di maglia la grandezza pilotante I1 che circola su R1.
7
esercitazioni
Coerentemente con le assegnazioni in figura si ottiene il seguente sistema risolvente:
 J1 ( R1 + R2 ) − J 2 R2 = VI

 J 2 R2 + R3 − J1 R2 − J3 R3 = E

J3 R3 − J 2 R3 = −VI − V1


J1 − J3 = I


V1 = hJ1

(
)
Risolvendo il sistema letteralmente si ottiene:
J1 =
J2 = −
(
)
J 2 R2 + R3 + IR3 − E
R2 + R3
( IR3 − E )( R3 + R1 + R2 + h ) − IR3
R1 + h
( R2 + R3 )( R1 + h )
Sostituendo i valori numerici si ottiene:
J 2 = −0.039
J1 = 0.161
J3 = −0.839
Quindi dall’equazione alla maglia in cui circola J3 si ha:
VI = 15.66
Si determini VI mediante il metodo dei potenziali di nodo e si confrontino i due procedimenti.
Esercizio 2.5
Per la rete riportata in figura si determini il circuito equivalente di Thevenin alla porta A – B.
R1
R3
I2
+
E1
hi2
R2
R4
E2
R5
A
E1 = 20 [v]
E2 = 5 [v]
R1 = 10 [Ω]
R2 = 50 [Ω]
R3 = 10 [Ω]
R4 = 20 [Ω]
R5 = 20 [Ω]
h=2
B
8
Analisi delle reti
Si determini il generatore E0 della rete equivalente di Thevenin.
La rete da considerare è la seguente:
R1
R3
I2
+
E1
R2
J1
J2
hi 2 V
R4
+ E2
VAB
A
B
Si osservi come la maglia contenente il generatore E2 risulti aperta; pertanto si può pensare di
risolvere il circuito con il metodo delle correnti di maglia, in quanto il sistema risolvente risulta costituito da 2 equazioni in due incognite.
Si assegnino le due correnti di maglia J1 e J2; con i versi di figura si ottiene il seguente sistema:
 ( R1 + R2 ) J1 − R2 J 2 = E1

 R2 + R3 + R4 J 2 − R2 J1 = V

J 2 = hI 2


I 2 = J1 − J 2

(
a
)
a
Dalle 3 e 4 si ha:
J2 =
h
J
1+ h 1
Sostituendo nelle prime due equazioni del sistema, semplificando e sostituendo i dati si ottiene:
J1 =
(1 + h ) E1
= 0.75 [A]
(1 + h )( R1 + R2 ) − hR2
J 2 = 0.5 [A]
L’equazione di Kirchhoff alle tensioni per la maglia aperta includente la porta A-B si scrive come:
VAB + E2 + VR = 0
4
Poichè VR = J 2 R4 , sostituendo si ricava:
4
E0 = VAB = –E2 – J2R4 = –15 [v]
La tensione ai capi del generatore pilotato di corrente vale:
(
)
V = R2 + R3 + R4 J 2 − R2 J1 = 2.5 [v]
9
esercitazioni
Calcolo di R0.
Per calcolare la resistenza della rete equivalente di Thevenin si consideri il seguente circuito:
R1
R3
I2
R2
J1
J2
R4
I0
hi 2
J3
A
B
Si osservi che a causa della presenza del generatore pilotato per valutare R0 occorre inserire tra i capi
A e B un generatore di “test”.
Applicando il metodo delle correnti di maglia e definendo J1, J2 e J3 come in figura si ottiene il
seguente sistema:
 J1 ( R1 + R2 ) − J 2 R2 = 0

 J 2 R2 + R3 + R4 − J1 R2 = V

J3 R4 − J2 R4 = V '


J 2 = h J1 − J 2


J3 = I 0

(
)
(
)
Dalla penultima equazione si ottiene:
J2 =
h
J
1+ h 1
e sostituendo:

h
 J1 ( R1 + R2 ) − 1 + h J1 R2 = 0

 h
J1 R2 + R3 + R4 − J1 R2 = V

1 + h
h

I 0 R4 −
J1 R4 = V '

1
+
h

(
)
Usando i valori numerici e semplificando si determina facilmente il valore di J1, che sostituito nella
3a equazione permette di ricavare:
R0 =
Spiegare fisicamente perchè R0 = R4 .
V'
= R4 = 20 [W]
I0
10
Analisi delle reti
La rete equivalente di Thevenin è schematizzabile come nella seguente figura:
R0
A
+
VAB
R5
B
Esercizio 2.6
Risolvere la seguente rete con i metodi delle correnti di maglia e dei potenziali di nodo:
R1
R3
I2
+
R2
E1
hi2
R4
+
R1 = 10 [Ω]
R2 = 50 [Ω]
R3 = 10 [Ω]
R4 = 20 [Ω]
E2
R5
R5 = 20 [Ω]
E1 = 20 [v]
E2 = 5 [v]
h=2
Risoluzione con il metodo delle correnti di maglia.
R1
R3
I2
+
E1
R2
Jb
Jc
hi 2
V
R4
Ja
+ E2
R5
Dopo aver assegnato le correnti di maglia si scriva il sistema risolvente. Con le scelte riportate in
figura si ottiene:
 ( R1 + R2 ) J b − R2 Jc = E1

 R2 + R3 + R4 Jc − R2 J b = V

 R4 + R5 J a − R4 Jc = E2

Jc = hI 2


I 2 = J b − Jc

(
(
)
)
esercitazioni
11
Dalle ultime due equazioni si ha:
Jb =
h +1
J
h c
Sostituendo nella 1a equazione e usando i valori numerici si ricava:
Jc = 0.5 [A]
Quindi:
J b = 0.75 [A]
V = 2.5 [V]
J a = 0.375 [A]
E5 = I 5 R5 [A]
I E = J b = 0.75 [A]
I R = Jb = 0.75 [A]
VR = R1I R = 7.5 [v]
VR = R2 I 2 = 12.5 [v]
I R = Jc = 0.5 [A]
VR = R3 I R = 5 [v]
I R = Jc − J a = 0.125 [A]
VR = R4 I R = 2.5 [v]
I E = J a = 0.375 [A]
I R = J a = 0.375 [A]
VR = R5 I R = 7.5 [v]
1
1
1
1
2
3
3
3
4
4
4
2
5
5
5
Risoluzione con il metodo dei potenziali di nodo.
In questo caso conviene trasformare il generatore di tensione reale E1, con in serie la resistenza
R1, i n un generatore di corrente reale I1 (con in parallelo la resistenza R1), e il generatore di tensione
reale E2 nel generatore di corrente reale I’2.
I1 e I’2 valgono rispettivamente:
E
I1 = 1 = 2 [A]
R1
I 2' =
E2
= 0.25 [A]
R5
12
Analisi delle reti
Assegnando i potenziali ai nodi come in figura si ottiene:
R3
V1
1
V3
2
I2
R1
I1
V2
R2
hi2
R4
3
0
V
V0
R5
I’2
 1
 1
1
1
1
1
+  V1 − V2 −  +  V3 = I1
 +
R3
 R1 R2 
  R1 R2 R3 

1
1

V2 − V1 = − hI 2
R3
R3


 1
1
1
1
1
 1
'
 R + R + R + R  V3 −  R + R  V1 = I 2 − I1
1
2
2
4
5
 1

1
I2 =
V1 − V3

R
2

(
)
Sostituendo la 4a equazione, utilizzando i valori numerici e semplificando si ha:
 0.22V1 − 0.1V2 − 0.12V3 = 2

−0.06V1 + 0.1V2 − 0.04V3 = 0
 0 12
 − . V1 + 0.22V3 = −1.75
da cui si ottiene:
Sostituendo si ha quindi:
V1 = 1.833V3 + 14.583
V3 = −2.504 [v]
V2 = 4.994 [v]
V1 = 9.993 [v]
Dai valori dei potenziali di nodo si calcolano
I 2 = 0.25 [A]
hI 2 = 0.5
e gli altri valori, uguali a quelli calcolati con il metodo delle correnti di maglia.
13
esercitazioni
Esercizio 2.7
Per la rete di figura si determinino le tensioni e le correnti in ogni ramo. Si effettui infine il bilancio
delle potenze.
I1
R1
R2
I
+
E
R1 = 60 [Ω]
R2 = 30 [Ω]
R3 = 20 [Ω]
h = 2 [Ω]
R3
+
V’1
E = 10 [v]
I = 1 [A]
V’1 = hI1
Si analizzi preliminarmente la struttura della rete.
mi = 3; n = 4; ni = 3; l = 6
Si ha che mi = ni.
Per la risoluzione di questa rete si utilizza il metodo dei potenziali di nodo.
Si faccia riferimento alla figura, in cui sono indicati anche i potenziali assegnati ai diversi nodi;
il sistema risolvente è:
I1
V1
+
E
R2
R1
V2
V3
I
R3
IE
+
V’1
IV1
V0
 1
1
1
1
 +  V1 − V2 − V3 = I E
R2
R1
 R1 R2 

 1
1
1

+  V2 − V1 = I


R2
 R2 R3 

1
1

V3 − V1 = IV ' − I

1
R1
R1

V1 = E


V3 = V1'

14
Analisi delle reti
Inoltre
I1 =
V1 − V3 E − hI1
=
, poiché V1 = 10 [v]
R1
R1
Da quest’ultima si ottiene:
I1 = 0.161 [A]
Quindi:
V3 = V1' = hI1 = 0.322 [v] e V2 = 16.060 [v]
Si ricava allora:
I 3 = 0.803 [A]
I 2 = 0.202 [A]
dall’equazione di Kirchhoff al nodo con potenziale V1:
I E = −0.041 [A], e analogamente
IV ' = 0.839 [A]; con una semplice differenza si ha:
1
VI = 15.738 [v].
Le tensioni ai capi delle resistenze R1, R2, R3 sono immediatamente calcolabili.
Bilancio delle potenze.
∑ Pg =∑ PR
EI E + VI I + V1' IV ' = VR I1 + VR I 2 + VR I 3
che diventa:
1
(
1
)
2
(
3
)
EI E + VI I + V1' IV ' = V1 − V3 I1 + V2 − V1 I 2 + V2 I 3
e, quindi,
1
15.598 ≅ 15.678 [W] = [W].
Esercizio 2.8
Per la rete di figura determinare il circuito equivalente di Thevenin ai morsetti A-B.
E
R2
+
A
R1
R3
I
R1 = 20 [Ω]
R2 = 30 [Ω]
R3 = 100 [Ω]
E = 10 [v]
B I = 1 [A]
15
esercitazioni
Calcolo del generatore E0 della rete equivalente di Thevenin.
Si faccia riferimento allo schema di figura.
E0 = VR − E = IR3 − E = 90 [V]
3
Calcolo della resistenza R0.
Si deve, preliminarmente, modificare la rete data cortocircuitando i generatori indipendenti di
tensione e aprendo i generatori di corrente; si ottiene così:
R2
A
R1
R3
R0
B
Si deduce subito che:
R0 = R3 = 100 [Ω]
La rete equivalente è allora:
A
+
E0
R0
B
Esercizio 2.9
Scrivere in forma letterale le equazioni risolventi la rete di figura col metodo delle correnti di maglia
e col metodo dei potenziali di nodo.
E2 +
R3
+
R1
+
E1
E4
R2
R4
Risoluzione col metodo delle correnti di maglia.
R5
I5
R6
16
Analisi delle reti
Si trasforma il generatore di corrente reale nel generatore di tensione equivalente:
E2 +
R3
Jc +
R1
R6
+
E1
R2
Ja
R5
E4
R4
Jb
E5
Jd +
in cui E5 = I 5 R5 .
Lo studio preliminare della rete permette di dedurre che essa è composta da l = 10 rami, da n =
7 nodi, e contiene mi = 4 maglie indipendenti.
Il sistema risolvente sarà costituito allora da 4 equazioni in altrettante incognite, e, con riferimento alla figura, si scriverà:

J a R1 − J b R6 = E1

J b ( R6 + R2 ) − J a R6 − Jc R2 = 0


 Jc R2 + R3 + R5 − Jb R2 − Jd R5 = E2 + E5

J d ( R4 + R5 ) − Jc R5 = E4 − E5

(
)
Risoluzione con il metodo dei potenziali di nodo.
Si trasformano i generatori di tensione in generatori di corrente e si ottiene:
I2
V1
V2
R3
I1
R1
R2
R6
I4
R4
con
I2 =
E
E2
E
; I1 = 1 ; I 5 = 5
R5
R3
R1
Il sistema risolvente è:
  1
1
1
1
1
+
+  − V2
= I1 − I 2
V1  +
R3
  R1 R2 R3 R6 

1
1
1
  1
 V2  R + R + R  − V1 R = I 4 − I 5 + I 2
5
3
3
4

I5
R5
17
esercitazioni
Esercizio 2.10
Dato il circuito di figura calcolare quale tensione deve produrre il generatore E1 affinchè chiudendo
il contatto t non si abbia passaggio di corrente nell’interruttore stesso.
t
R1
+
R2
R4
R5
+
E2
R3
E1
+
E3
R6
R1 = 50 [Ω]
R2 = 5 [Ω]
R3 = 40 [Ω]
R4 = 20 [Ω]
R5 = 20 [Ω]
R6 = 5 [Ω]
E2 = 30 [v]
E3 = 40 [v]
R1
R2
+
I
t
R3 V’A
R4
A
R5
+
E2
V’’ A
E1
+
R6
E3
B
Si osservi lo schema; si indichi con I la corrente sull’interruttore; con V’AB la tensione ai capi della
resistenza R3, pari a quella del contatto t a interruttore aperto; e con V’’AB la tensione alla sezione A –
B dello schema, cioè quella tra il terminale della R4 non connesso all’interruttore e il nodo B.
Se chiudendo l’interruttore t non si deve avere passaggio di corrente nell’interruttore stesso si
deve avere:
V’AB(I = 0) = V’’AB(I = 0)
Se la corrente che circola sull’interruttore chiuso è nulla tutta la corrente che attraversa la R1 passerà
sulla R3; quindi:
'
VAB
(0) =
E1 R3
R1 + R3
Si osservi poi che se I = 0 la caduta di tensione su R4 è nulla e che si ha:
Perciò:
''
VAB
(0) = E3 = 40 [v]
E1 = 90 [v]
18
Analisi delle reti
Esercizio 2.11
Determinare l’energia immagazzinata in ciascuno dei condensatori della rete in regime stazionario.
3 mF
3k Ω
6k Ω
5k Ω
5 mA
5k Ω
2 mF
In regime stazionario si può sostituire ciascun condensatore con un circuito aperto. L’energia immagazzinata vale:
1
W = CV 2
2
dove C è la capacità del condensatore e V è la tensione ai suoi capi.
Si ottiene il seguente schema:
V1
I1
3k Ω
6k Ω
5k Ω
5 mA
5k Ω
V2
La corrente I1 si può calcolare con il metodo del partitore di corrente:
I1 =
5 ⋅ 10 3
3
3
3 ⋅ 10 + 5 ⋅ 10 + 5 ⋅ 10
3
⋅ 5 ⋅ 10 −3 = 1.923 ⋅ 10 −3 [A]
I1 = 1.923 [mA]
Le tensioni V1 e V2 sui condensatori si calcolano facilmente e valgono, rispettivamente:
V1 = 5.769 [v] e V2 = 9.615 [v]
Per cui le energie immagazzinate nei due condensatori sono:
W1 = 50 [mJ] e W2 = 92 [mJ]
19
esercitazioni
Esercizio 2.12
Ricavare il circuito equivalente di Thevenin ai morsetti A-B del circuito di figura.
A
R
R
+
R
E
R
R
B
Calcolo del generatore E0 della rete equivalente.
Da considerazioni sulla simmetria della rete rispetto il ramo contenente il generatore E si ricava:
E0 = 0
si dimostri tale risultato usando l’analisi circuitale.
Calcolo della resistenza Req della rete equivalente.
Si cortocircuita il generatore E, ottenendo la rete seguente:
A
R
R
R
R
R
B
Considerando le due resistenze con un terminale al nodo A e quella connessa tra i restanti terminali
delle stesse si ottiene un triangolo, costituito da tre resistori di uguale valore R; pertanto la stella a
esso equivalente sarà pure costituita da tre resistenze uguali e di valore:
R1 = R2 = R3 =
R⋅R R
=
3R
3
20
Analisi delle reti
Sostituendo la stella i cui componenti sono stati ora calcolati al triangolo si ottiene il seguente schema:
A
R/3
R/3
R/3
R
R
B
Semplici calcoli di resistenze in serie e in parallelo consentono ora di derivare la resistenza Req:

R 
R
R+ R+ 

3
3  R 2R
R
R 
=R
Req = +
= +
3 3
3

R
2 R + 
3

La rete equivalente di Thevenin è perciò:
A
Req
B
Esercizio 2.13
Calcolare la tensione dei punti A, B, e C del circuito in figura con i dati riportati:
A1
+
E1
R4
R2
+
R1
R3
E2
21
esercitazioni
E1 = 5 [v]
E2 = 3 [v]
R1 = 1 [kΩ]
R2 = 2 [kΩ]
R3 = 3 [kΩ]
R4 = 4 [kΩ]
A1 = 10 [mA]
Si sceglie di adoperare il metodo dei potenziali di nodo, osservando che è possibile eliminare un nodo
(improprio) applicando la trasformazione di Thevenin-Norton al generatore di tensione E2.
Si ottiene così il seguente schema:
IE
A
A1
+
E1
R2
C
B
R1
con A2 =
R4
R3
A2
E2
= 1 [mA].
R3
Il sistema risolvente è il seguente:







 1
 R2


1
1
VA − VC = A1 + I E
R4
R4
 1
1
1
 R + R  VB − R VC = − A1
 1
2
2
+
1
1
1
1
+  VC − VB − VA = A2
R3 R4 
R2
R4
VA = E1
a
Sostituendo la 4 equazione e usando i valori numerici si ottiene:

1.25 ⋅ 10 −3 − 2.5 ⋅ 10 −4 VC = 1 ⋅ 10 −2 + I E

1.5 ⋅ 10 −3 VB − 5 ⋅ 10 −4 VC = −1 ⋅ 10 −2


−3
−4
−3
−3
1.083 ⋅ 10 VC − 5 ⋅ 10 VB − 1.25 ⋅ 10 = 1 ⋅ 10
22
Analisi delle reti
Dalla 2a si ricava:
VC = 3VB + 20
Si ottiene, poi:
VB = −7.184 [v]
VC = −1.552 [v]
Esercizio 2.14
Determinare il circuito equivalente di Norton ai morsetti A – B della rete elettrica riportata in figura.
R2
A
R1
I
R4
+
E
R3
B
R1 = 4 [Ω]
R2 = 8 [Ω]
R3 = 8 [Ω]
R4 = 5 [Ω]
E = 12 [v]
I = 2 [A]
Per determinare il circuito equivalente di Norton ai morsetti A – B della rete occorre calcolare i valori
del generatore di corrente I0 e della resistenza R0.
Calcolo di I0.
Si faccia riferimento alla seguente rete:
R2
I
R1
I0
R4
+
E
A
R3
B
Dopo le opportune semplificazioni, e definendo:
Rs = R2 + R3 = 16 [Ω]
23
esercitazioni
I1 =
E
= 3 [A] e
R1
I p = I + I1 = 5 [A]
si ottiene:
I0 =
R1
I = 1 [A]
R1 + Rs p
Calcolo di R0.
La rete da analizzare è la seguente:
R2
A
R1
R4
R0
R3
B
Si osserva che:
R0 =
( R1 + R2 + R3 ) R4 = 4 [Ω]
( R1 + R2 + R3 ) + R4
Pertanto la rete equivalente di Norton è la seguente:
A
I0
R0
B
Esercizio 2.15
Per il circuito riportato in figura determinare la corrente in tutti i resistori.
1 Ω
2 Ω
1 Ω
2 Ω
2 Ω
2A
1Ω
24
Analisi delle reti
Si osservi come tra i punti A, B e C vi sia un triangolo di resistenze, trasformabile in una stella a esso
equivalente:
1 Ω
B
2 Ω
A
1 Ω
2 Ω
2 Ω
C
1 Ω
2A
A
A
2 Ω
R1
1 Ω
R2
B 2 Ω C
R3
B
C
Per calcolare i valori delle resistenze R1, R2 ed R3 si applicano le formule di trasformazione, e si ha:
R1 =
1⋅ 2
= 0.4 [Ω]
2 +1+ 2
R2 =
2⋅2
= 0.8 [Ω]
2 +1+ 2
R3 =
2 ⋅1
= 0.4 [Ω]
2 +1+ 2
Con questa trasformazione si ha:
D
I1
I2
R1
A
1 Ω
B
I3
R2
R3
C
I4
2A
2 Ω
E
1 Ω
25
esercitazioni
Trasformando il generatore di corrente in un generatore di tensione equivalente si ha:
D
I2
I1
I3
R2
R1
R3
B
A
C
2 Ω
1 Ω
1 Ω
+
Eeq
E
con Eeq = 2 ⋅ 2 = 4 [v].
Infine, calcolando le resistenze equivalenti alle diverse serie, e cioè:
Rs = R1 + 1 = 1.4 [Ω]
1
Rs = R2 + 2 = 2.8 [Ω]
2
Rs = R3 + 1 = 1.4 [Ω]
3
allora:
Eeq
VDE =
Rs
1
I1 =
Siccome:
3
VDE
= 0.571 [A]
Rs
Eeq + I 2 Rs − VDE = 0
2
I 2 = −1.143 [A]
I3 =
2
= 0.8 [v]
1
2
1
1
1
+
+
Rs Rs
Rs
VDE VDE
=
= I1 = 0.571 [A]
Rs
Rs
3
1
I 4 = 2 + I 2 = 0.857 [A]
Inoltre:
VAB − I1 ⋅ 1 + I 4 ⋅ 2 = 0
26
Analisi delle reti
da cui:
VAB = −1.143 [v]
Ib = −
VAB
= 0.571 [A]
2
I d = I1 = 0.571 [A]
I a = I b − I d = 0 [A]
I f = I 3 = 0.571 [A]
I c = I f = 0.571 [A]
I e = I 4 = 0.857 [A]
Esercizio 2.16
Per il circuito di figura determinare:
1) il circuito equivalente di Norton ai morsetti a – b;
2) la resistenza RL da inserire ai morsetti a – b in modo che essa assorba la massima potenza.
R1
a
+
E
+
Vab
I
βI
Vab
R2
b
Calcolo della corrente di cortocircuito I0.
Per il calcolo della corrente di cortocircuito I0 si faccia riferimento al seguente schema:
R1
+
E
a
+
I
Vab
βI
I0
R2
b
Si ha:
I0 = β I
E − IR1 − Vab = 0
In questo caso Vab = 0 , quindi:
I=
E
R1
I0 =
βE
R1
27
esercitazioni
Calcolo della resistenza R0 della rete equivalente di Norton.
Per il calcolo della resistenza R0 della rete equivalente di Norton ci si riferisca alla seguente
rete:
a I1
IR2
+
R1
I
R2
βI
Vab
+
E1
b
R0
Poiché la rete presenta generatori pilotati, che non devono essere modificati, per il calcolo di R0 occorre sollecitare il circuito con un generatore di “test” noto E1.
Si ha:
R0 =
E1
I1
Dall’esame del circuito si deduce:
Vab = E1
I=−
E1
R1
I1 = I R − β I = E1
2
R1 + β R2
R1 R2
Quindi:
R0 =
R1 R2
R1 + β R2
Il circuito equivalente di Norton ai morsetti a – b è quindi:
a
I0
R0
b
28
Analisi delle reti
Esercizio 2.17
Per il seguente circuito determinare la rete equivalente di Thevenin ai capi del resistore R3.
R2
R3
R4
E
+
J
R5
E = 24 [v]
J = 1 [mA]
R2 = 10 [kΩ]
R3 = 4 [kΩ]
R4 = 40 [kΩ]
R5 = 20 [kΩ]
Calcolo del generatore Eeq.
Per questo scopo ci si riferisca alla seguente rete:
A E eq B
R2
IR5
R4
E
+
J
R5
IR4
Si deduce:
Eeq = VA − VB
VA = −VR = −
4
ER4
= −19.2 [v]
R4 + R2
VB = R5 J = 20 [v]
Quindi:
Eeq = −39.2 [v]
Calcolo della resistenza Req.
Per il calcolo della resistenza Req occorre cortocircuitare i generatori indipendenti di tensione e
aprire i generatori indipendenti di corrente; pertanto la rete diventa:
29
esercitazioni
Req
R2
A
B
R4
Req =
R5
R2 R4
+ R5 = 28 [kΩ]
R2 + R4
Quindi, considerando collegato il carico R3, si ha:
Req
Eeq
A
+
R3
B
Esercizio 2.18
Determinare il circuito equivalente di Thevenin della rete di figura:
a
ix
4i x
10 Ω
8 Ω
b
Calcolo di Eeq.
Poiché il circuito è privo di generatori indipendenti Eeq = 0 .
Calcolo di Req.
Per calcolare Req si applica un generatore di test del valore I0 = 1 [A] come descritto dal seguente
schema:
a
ix
4i x
10 Ω
8 Ω
V0
b
I0
30
Analisi delle reti
Applicando l’analisi nodale:

V0
 I 0 + ix = 4ix +
10

V

ix = − 0

8
Si ottiene:
I 0 = 3ix +
V0
3V V
11V0
=− 0 + 0 =−
= −0.275V0
10
8 10
40
e quindi:
Req =
V0
= −3.636 [Ω]
I0
Il valore negativo ottenuto per la resistenza dice che, secondo la convenzione degli utilizzatori, il
circuito proposto eroga potenza.
Naturalmente i resistori non possono erogare potenza, e quindi a erogare potenza è il generatore
dipendente.
Questo è un esempio di come la combinazione di un generatore dipendente e di resistori possa
essere usata per simulare una resistenza di valore negativo.
Esercizio 2.19
Calcolare la tensione ai capi A – B del seguente circuito applicando il teorema di Millman:
A
R1
I
R2
+
E
B
E = 6 [v]
I = 1 [A]
I1 = 2 [A]
R1 = 1 [kΩ]
R2 = 2 [kΩ]
Utilizzando direttamente la formula del teorema di Millman si ha:
E
+I
R2 1
=
= 2002 [v]
1
1
+
R1 R2
I+
VAB
I1
31
esercitazioni
Esercizio 2.20
Determinare le tensioni e le correnti in tutti i rami della rete di figura.
R3
R1
R4
R2
I
+
E
I = 2.5 [A]
E = 3 [v]
R1 = 6 [Ω]
R2 = 8 [Ω]
R3 = 20 [Ω]
R4 = 12 [Ω]
Considerando la presenza di un parallelo tra due resistenze e di una serie tra altre due si perviene alla
seguente semplificazione della rete data:
Req1
+
Req
VI
E
I
in cui:
Req =
R1 R2
= 3.428 [Ω]
R1 + R2
Req = R3 + R4 = 32 [Ω]
1
Trasformando il generatore di corrente in uno equivalente di tensione si ottiene la seguente rete:
Req
Eeq
Ia
Req1
+
+
E
in cui:
Eeq = IReq = 8.57 [v]
32
Analisi delle reti
Dall’equazione alla maglia si ottiene:
Eeq − E
Ia =
= 0.157 [A]
Req + Req
1
Quindi si ha:
VR = VI = E + I a Req = 8.024 [v]
1
eq
I R = I R = I E = I a = 0.157 [A]
3
4
VR = I R R3 = 3.14 [v]
3
3
VR = I R R4 = 1.884 [v]
4
4
VR = VR = VR = 8.024 [v]
1
2
IR =
1
IR =
2
eq
VR
1
R1
VR
2
R2
= 1.337 [A]
= 1.003 [A]
Esercizio 2.21
Determinare la resistenza del resistore R affinchè sia massima la potenza dissipata in esso.
R1
R2
R4
+
E1
H
I
+
R3
+
E2
R
E3
K
Si applichi il teorema del massimo trasferimento di potenza dopo aver determinato la rete equivalente
di Thevenin ai morsetti H-K del circuito dato.
La condizione da imporre è: Req = R.
Calcolo della Req.
33
esercitazioni
Si cortocircuitano i generatori di tensione e si aprono quelli di corrente:
R1
R2
H
R4
R3
K
Ovvero la rete diviene la seguente:
R1 + R2
H
R4
K
Si ottiene:
Req =
(
R4 R1 + R2
)
R4 + R1 + R2
da cui, per ottenere il risultato cercato, basta porre:
R=
(
R4 R1 + R2
)
R4 + R1 + R2
Req
+
E
R
34
Analisi delle reti
Esercizio 2.22
Determinare l’equivalente di Thevenin ai morsetti a-b del circuito di figura:
6Vx
+
10 Ω
8 Ω
a
+
VI
8 A Vx
6 Ω
10 Ω
b
Per calcolare il valore di Eeq si valuta Vab a circuito aperto nella rete di partenza.
6Vx
+
J3
+
J1
VI
8 A Vx
8 Ω
a
10 Ω
6 Ω
J 2 10 Ω
b
Applicando il metodo delle correnti di maglia si ottiene:

6 J1 − 6 J2 = Vx

 6 + 10 + 10 J 2 − 6 J1 − 10 J3 = 0

10 J3 − 10 J 2 = 6Vx


J1 = 8

(
)
a
Usando la 4 equazione e applicando poi il metodo di sostituzione si ottiene:
 26 J 2 − 10 J3 = 48

26 J 2 + 10 J3 = 288
che risolto dà:
J3 = 12 [A]
J 2 = 6.461 [A]
35
esercitazioni
Si ha quindi:
Vab = 64.61 [v]
Calcolo di Req.
Per il calcolo di Req si fa riferimento al seguente circuito:
6Vx
+
J2
Vx
8 Ω I0 a
10 Ω
6 Ω
J1
+
10 Ω
V0
J3
b
Si può scrivere il seguente sistema:
(
)
 6 + 10 + 10 J1 − 10 J 2 − 10 J3 = 0

10 J2 − 10 J1 = 6Vx


10 + 8 J3 − 10 J1 = −V0


Vx = −6 J1

(
)
Si può ricavare:
J 2 = −2.6 J1
e quindi:
16.08 J3 = −V0
Osservando che I1 = 1.923 si ricava:
Req =
V0
= 16.08 [Ω]
I0
Esercizio 2.23
Usando il teorema di Norton calcolare il circuito equivalente ai morsetti a-b della rete il cui schema
è riportato in figura:
36
Analisi delle reti
4Ix
Ix
a
6 Ω
+
16 Ω
10 v
b
Calcolo della corrente di corto circuito Icc.
Per il calcolo di Icc ci si riferisce alla seguente rete:
4Ix
Ix
a
6 Ω
+
16 Ω
Icc
10 v
b
I x = 1.667 [A]
I cc = I x + 4 I x = 8.335 [A]
Calcolo di Req.
Data la presenza di un generatore pilotato per il calcolo di Req si inserisce un generatore di test V0:
4Ix
Ix
a
6 Ω
I0
+
16 Ω
V0
b
37
esercitazioni
Ix = −
V0
6
I 0 = −4 I x − I x = 0.833V0
Req =
V0
= 1.2 [Ω]
I0
Esercizio 2.24
Facendo uso dell’analisi alle maglie calcolare la corrente I0 nel circuito di figura:
I0
R1
R4
R3
+
E
+
R2
hI0
R1 = 1 [Ω]
R2 = 3 [Ω]
R3 = 6 [Ω]
R4 = 2 [Ω]
h = 2 [Ω]
E = 20 [v]
Dopo aver definito le correnti di maglia come in figura si può scrivere il seguente sistema risolvente:
I0
R1
+
E
J2
R4
R3
J1
+
R2
)
 R1 + R2 J1 − R1 J 2 − R2 J3 = E

 R1 + R4 + R3 J 2 − R1 J1 − R3 J3 = 0

 R2 + R3 J3 − R2 J1 − R3 J 2 = − hI 0

I 0 = J1 − J 2

(
(
(
J3
)
)
hI 0
38
Analisi delle reti
a
Usando la 4 equazione e riordinando i termini si ottiene:
4 J1 − J 2 − 3 J3 = 20

 9 J 2 − J1 − 6 J3 = 0
 9J J 8J 0
 3− 1− 2 =
da cui:
J1 = 10 [A]
J 2 = 4.545 [A]
J3 = 5.152 [A]
Si ha quindi:
I 0 = 5.455 [A]
Esercizio 2.25
Per la rete illustrata in figura:
1) si determinino tutte le correnti di lato;
2) si verifichi il risultato ottenuto per la corrente nel resistore R6 determinando il generatore equivalente di Norton ai capi del resistore stesso;
3) si verifichi il principio di conservazione della potenza.
J5
R5
R3
R7
+
E1
R2
R6
+
E2
R4
R2 = 2 [kΩ]
R3 = 4 [kΩ]
R4 = 5 [kΩ]
R5 = 1 [kΩ]
R6 = 2 [kΩ]
R7 = 8 [kΩ]
E1 = 6 [v]
E7 = 8 [v]
E2 = 5 [v]
J5 = 1 [mA]
+
E7
39
esercitazioni
Per semplificare la risoluzione del circuito si osservi che si può applicare il teorema di Thevenin alla
porta AB:
IE1
IAB A
IR2
R2
+
E1
+
E2
B
I componenti dello schema equivalente di Thevenin valgono:
VAB = E1
RAB = 0 [Ω]
La rete così trasformata è quindi riportata nella seguente figura:
V I5
IR5
R5
J5
IAB
IR3
J5
IR7
R3
IR6
R6
J4
VAB
R7
IE7
+
E7
J7
R
IR4
Per la determinazione delle correnti di lato si sceglie di adoperare il metodo delle correnti di maglia,
e, definendo queste ultime come indicato nella suddetta figura, si scrive il seguente sistema risolvente:
(
)
 R3 + R6 + R4 J 4 − R3 J5 − R6 J 7 = VAB

R3 + R5 J5 − R3 J 4 = VI

5

R
+
R
J
R
J
E
−
=
−

6
7
7
6 4
7

−3
J5 = 1 ⋅ 10

(
(
)
)
Sostituendo i valori numerici si ottiene:
J 7 = 5.5 J 4 − 5 ⋅ 10 −3
J 4 = 7.924 ⋅ 10 −4 [A]
J 7 = −6.42 ⋅ 10 −4 [A]
40
Analisi delle reti
Considerando nuovamente il circuito equivalente di Thevenin alla porta AB si può scrivere la seguente equazione:
E2 − R2 I R − VAB = 0
2
da cui:
I R = −5 ⋅ 10 −4 [A]
2
Si ha inoltre:
I AB − I E − I R = 0
1
2
e si ha:
I E = 1.292 ⋅ 10 −3 [A]
1
Si calcolano, quindi:
I E = −5 ⋅ 10 −4 [A]
2
I R = −2.076 ⋅ 10 −4 [A]
3
I R = 1 ⋅ 10 −3 [A]
5
I R = 7.924 ⋅ 10 −4 [A]
4
I R = 1.434 ⋅ 10 −3 [A]
6
I R = −6.42 ⋅ 10 −4 [A]
7
I E = −6.42 ⋅ 10 −4 [A]
7
Calcolo del generatore equivalente di Norton ai capi di R6.
Si comincia con il determinare la corrente Icc riferendosi al seguente schema:
R5
J5
R3
+
E1
R7
R2
Icc
+
E2
R
+
E7
41
esercitazioni
Applicando di nuovo il teorema di Thevenin alla porta AB si ottiene:
VI5
R5
J5
J5
R3
R7
+
VAB
J4
Icc
+
E7
J7
R4
La risoluzione di questo circuito viene ancora effettuata con il metodo delle correnti di maglia:
(
(
)
)
 R3 + R4 J 4 − R3 J5 = VAB

 R3 + R5 J5 − R3 J 4 = VI5

R7 J7 = − E7


J5 = 1 ⋅ 10 −3

da cui si ha:
J 4 = 0.0011 [A]
J 7 = −1 ⋅ 10 −3 [A]
I cc = 2.1 ⋅ 10 −3 [A]
Determinazione di Req.
Per la determinazione di Req ci si riferisce al seguente schema:
R5
R3
R7
R2
Req
R
42
Analisi delle reti
che equivale alla rete:
R3
R7
R eq
R4
Req =
(
R7 R3 + R4
) = 4.235 ⋅103 [Ω]
R7 + R3 + R4
La rete di Norton connessa al carico R6 è quindi:
IReq
Icc
IR6
R6
Req
da cui:
IR =
6
Req I cc
Req + R6
= 1.426 ⋅ 10 −3 [A]
La leggera differenza tra il valore ottenuto precedentemente e quest’ultimo dipende dalle approssimazioni effettuate durante il calcolo.
Bilancio delle potenze.
Il bilancio delle potenze si esprime come:
5
( )
R4 I R2
4
R5 I R2
5
E1I E + E2 I E + VI J5 + E7 − I E =
=
1
2
R2 I R2
2
R3 I R2
3
+
+
7
+
+ R6 I R2 + R7 I R2
Per la sua valutazione occorre determinare il valore di VI :
5
Sostituendo i valori numerici si ha:
VI = 1.83 [v]
5
0.012 = 0.012 [W] = [W]
6
7
43
esercitazioni
Esercizio 2.26
Per la rete riportata in figura si determinino tutti i coefficienti della matrice D assumendo che le
uscite che interessano siano le seguenti grandezze: V1, Va, I3, Ie.
+e
R2
I3 Ie
R1
V1
R3
Va
R4
R5
a
R1 = 3 [kΩ]
R2 = 9 [kΩ]
R3 = 1.8 [kΩ]
R4 = 2 [kΩ]
R5 = 4 [kΩ]
a = 10 [mA]
e = 3 [v]
Si definiscano, per cominciare, i vettori d’ingresso e di uscita, rispettivamente:
s=
e
y=
e
a
V1
Va
I3
Ie
Per il calcolo dei coefficienti D11 e D21 occorre supporre l’ingresso s2 = 0, quindi:
a = 0
D11 =
D21 =
V1
e
Va
e
s2 = 0
s2 = 0
In quest’ipotesi la rete di partenza diventa la seguente:
R2
+e
I3 Ie
R1
V1
R3
R4
R5
44
Analisi delle reti
Si ricava immediatamente:
V1 = 0
Va = V3
Dopo aver determinato i valori numerici dei due coefficienti si determinino anche tutti gli altri termini della matrice D .
Esercizio 2.27
Si determini la matrice uscita-ingresso per la rete schematizzata in figura.
+ e1
I3 R3
I1
R1
R5
+
e2
R2
R4
+
e3
I6
R6
e1 = 3 [v]
e2 = 6 [v]
e3 = 9 [v]
R1 = 30 [Ω]
R2 = 80 [Ω]
R3 = 60 [Ω]
R4 = 30 [Ω]
R5 = 80 [Ω]
R6 = 60 [Ω]
Si definiscano i vettori di ingresso e di uscita:
e1
s = e2
e3
I1
y = I3
I6
Il legame tra i vettori di ingresso e di uscita è dato dalla:
y = D ⋅s
Per il calcolo dei diversi termini della matrice D occorre supporre che agisca soltanto uno dei generatori di tensione, cortocircuitando gli altri due.
Per il calcolo di D11, D21 e D31 si ponga s2 = e2 = 0 e s3 = e3 = 0.
45
esercitazioni
Si ottiene quindi la seguente rete:
+ e1
I3 R3
R5
I1
R1
I6
R2
R4
R6
Data la presenza del cortocircuito in parallelo a R2 si ha:
e1
R1
I1 =
Quindi:
D11 =
I1
e1
e2 = 0
e3 = 0
1
= 0.033 [S]
R1
=
Inoltre:
D21 =
I3
e1
D31 =
I6
e1
e2 = 0
e3 = 0
e2 = 0
e3 = 0
=0
=0
Per il calcolo dei termini D12, D22 e D32 si ponga s1 = e1 = 0 e s3 = e3 = 0.
Si ottiene quindi la seguente rete:
I3 R3
I1
R1
R5
I6
+
R2
e2
R4
R6
Si determinino, dopo quest’esemplificazione, i valori di tutti i restanti termini della matrice D
richiesta.