APPUNTI DI MECCANICA QUANTISTICA
ripasso sui fenomeni ondulatori.
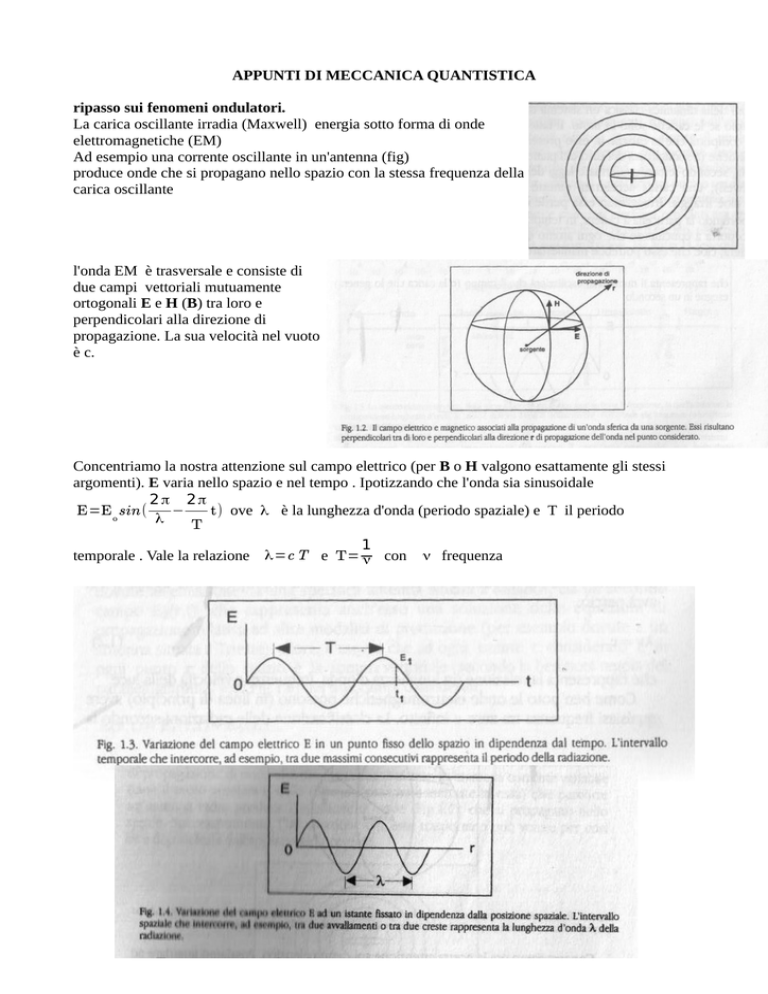
La carica oscillante irradia (Maxwell) energia sotto forma di onde
elettromagnetiche (EM)
Ad esempio una corrente oscillante in un'antenna (fig)
produce onde che si propagano nello spazio con la stessa frequenza della
carica oscillante
l'onda EM è trasversale e consiste di
due campi vettoriali mutuamente
ortogonali E e H (B) tra loro e
perpendicolari alla direzione di
propagazione. La sua velocità nel vuoto
è c.
Concentriamo la nostra attenzione sul campo elettrico (per B o H valgono esattamente gli stessi
argomenti). E varia nello spazio e nel tempo . Ipotizzando che l'onda sia sinusoidale
2π 2π
E=E o sin(
−
t) ove λ è la lunghezza d'onda (periodo spaziale) e T il periodo
λ
T
1
temporale . Vale la relazione λ=c T e T= ν con
ν frequenza
caratteristica essenziale dei campi EM è la linearità delle equazioni di Maxwell . Se ad esempio
E 1 (r ,t ) è un campo che rappresenta una soluzione delle equazioni per una certa modalità di
produzione (ad esempio un onda emessa da usa stazione radio di Trieste) ed E 2 (r ,t ) è un'onda
che rappresenta un campo soluzione delle equazioni per un'altra modalità di produzione (ad
esempio il campo prodotto da un 'antenna radio di Roma, allora il campo in ogni posizione r e ad
ogni istante t è E (r ,t )=E 1 (r , t )+E 2 (r ,t )
Più in generale se E 1 ed E 2
sono due distinte soluzioni delle equazioni di Maxwell allora una
qualsiasi combinazione lineare α E 1 +βE 2 è soluzione.
Infine è fondamentale ricordare l'aspetto di maggior rilievo fisico è che le onde EM trasportano
energia e quantità di moto . Nel caso delle onde EM la densità di energia in un punto e in certo
1 2
2
istante è proporzionale alla somma dei quadrati delle ampiezze di E e B ( w=ε0 E + μ B ). Nel
0
vuoto tali densità risultano della stesso valore, cosicché si può dire che in un volume piccolo (in
modo che E non vari apprezzabilmente) l'energia è proporzionale al prodotto del volume per
E
2
.
La figura rappresenta la densità di energia nei vari punti di un raggio di propagazione. Come si vede
2
essa varia da punto a punto nello spazio (e nel tempo ) con continuità . Il prodotto E Δr
rappresenta l'energia concentrata in quell'intervallo
Diffrazione e interferenza
Fenomeni peculiare e caratteristico di tutti i fenomeni ondulatori.
É di fondamentale importanza che rilevare che la possibilità di vedere la manifestazione di questi
fenomeni è legata in modo cruciale alle dimensioni degli ostacoli: solo se questi hanno dimensione
paragonabile a λ essi si manifestano in modo evidente.
Il primo si manifesta come
deviazione dalla propagazione
rettilinea nel momento in cui l'onda
incontra un ostacolo.
Il secondo quando due
onde propagano nella
stessa regione dello spazio
sovrapponendosi e
sommandosi
vettorialmente.
In entrambe le figure le zone ombreggiate rappresentano la densità di energia nei vari punti. Una
lastra fotografica messa al posto dello schermo resterà maggiormente impressionata dove l'altezza
della figura di diffrazione o di interferenza è maggiore.
Polarizzazione.
Una caratteristica delle onde trasversali (in cui la perturbazione è perpendicolare alla direzione di
propagazione ) è che esse possono essere polarizzate: il vettore E ha una giacitura precisa:
• polarizzazione piana: E giace ed oscilla su un piano: un osservatore investito dall'onda
“vede” E oscillare lungo una retta
• polarizzazione circolare o ellittica: un osservatore investito dal''onda vede la freccia di E
percorrere una circonferenza o rispettivamente un'ellisse.
Consideriamo il solo campo E di due onde (EM) polarizzate lungo un piano piano (per brevità due
onde piane) della stessa ampiezza e frequenza (e quindi lunghezza d'onda) che propagano nella
stessa direzione ; poiché il campo totale è la somma vettoriale delle due onde, se esse sono “in fase”
il campo totale avrà
ampiezza doppia ( e
densità di energia
quadrupla), se esse sono
sfasate di mezza
lunghezza d'una (“in
opposizione di fase ) il
campo totale sarà nullo
Se i campi (piani ) da sommare hanno
giaciture diverse, applicando la regola del
parallelogramma si otterranno situazioni
diverse. Ad esempio se i piani (sempre
della stessa lunghezza d'onda e
ampiezza) sono perpendicolari tra loro e
“in fase” E v nel piano xz e E o nel
piano yz
si combineranno in un'onda piana
E 45=E v +E o lungo la diagonale del piano xy
E' importante, per quanto seguirà, sottolineare la possibilità che l'intensità un vettore E* arbitrario
di intensità ( ampiezza dell'onda ) E* sia espresso come prodotto di un vettore E un'intensità
standard E per un' opportuna costante cioè E*=aE. Poiché la densità di energia e quindi l'intensità
2
dell'onda è proporzionale al quadrato dell'ampiezza l'intensità di E* è a volte quella standard.
E Se E=1 allora a
2
è direttamente l'intensità di E*
In particolare se E 45 , E v
e Eo
infatti dal teorema di Pitagora
1 2 1 2 1 2 1 2
2
E 45= E v − E o = E + E =E
2
2
2
2
se lo sfasamento
è
Eo
e Ev
λ
2
sono tre vettori standard
E 45=
1
√2
Ev +
1
√2
Eo
la situazione sarà dalla dalla successiva figura
in tal caso il campo totale oscillerà su un piano a 135°
E 135=
1
√2
E v−
1
√2
Eo
Se si cambia la fase relativa di uno rispetto all'altro si otterranno polarizzazioni differenti
Noi useremo solo il caso della polarizzazione piana. E' estremamente importante ribadire che
qualunque campo di ampiezza standard può essere scritto come combinazione lineare di due campi
standard della stessa frequenza del campo totale, in fase tra loro e mutuamente ortogonali lungo due
piani qualsiasi arbitrariamente orientati
Vale ancora la pena notare che se l'ampiezza standard è 1 allora a
2
2
e b
2
sono le intensità
2
delle onde “componenti” e a +b =1 .
Filtri polaroid
la luce normale, sovrapposizione di un numero enorme di campi e emessi da sorgenti incoerenti
non è né monocromatica (una sola lunghezza d'onda) né polarizzata. Vale la pena di ricordare che
ciò che colpisce i nostri occhi è la somma vettoriale di questo enorme numero di campi E di
frequenza , giacitura e ampiezza diversa. Non si hanno pertanto fenomeni misurabili di interferenza,
poiché il campo totale cambia continuamente. Ciò che rimane costante e che è ciò che i nostri occhi
o altri strumenti ottici
“misurano”, è l'intensità
media della radiazione.
Se faccio passare la luce
in una lamina polaroid
(FP) la luce esce
polarizzata, cioè il vettore
E oscilla su un piano
parallelo al filtro.
Ponendo sul cammino del fascio un secondo FP , si ha che l'intensità del fascio che attraversa FP è
2
data dalla legge di Malus I =I o cos θ ove I o è l'intensità del fascio incidente (quello
uscente dal I° FP) e θ l'angolo tra il piano di polarizzazione dei due filtri. La formula si ricava
immediatamente da quanto descritto in precedenza.
E' sorprendente notare che interponendo un terzo FP e facendolo ruotare tra due FP orientati a 90°
la luce passi ( variando di intensità), mentre non passa se lo togliamo. Questo è un fenomeno assai
contro- intuitivo: siamo portati istintivamente a pensare che più ostacoli si frappongono , più
difficile è il passaggio.
D'ora in poi supporremo che la luce o l'onda EM “in ingresso” sia stata preventivamente
polarizzata tramite un FP, che quindi non verrà rappresentato nelle figure .
I cristalli birifrangenti
Più versatili dei FP sono i cristalli birifrangenti (CBR) . Questa versatilità consiste nel fatto che
tutto il fascio attraversa il cristallo.
in particolare :
• un raggio polarizzato verticalmente attraversa il cristallo senza essere deviato (raggio
ordinario)
• un raggio polarizzato orizzontalmente vie ne deviato ( raggio straordinario)
• un raggio polarizzato che forma un angolo θ col piano del cristallo viaggia sia sul
percorso ordinario che su quello straordinario.
L'intensità del raggio O è ancora
in accordo con la legge di
Malus : quella del raggio S è
(per la conservazione dell'energia
2
3
I =I o −I o cos θ=I o sin θ .
In particolare se l'angolo è 45°
1
I = I o per entrambi i raggi
2
Analisi quantistica dei fenomeni ondulatori
la descrizione della radiazione come costituita da fasci di fotoni obbliga a rivedere alla luce di tale
descrizione i fenomeni sin qui analizzati in chiave completamente classica.
Iniziamo quindi spedendo un fascio di luce polarizzata verticalmente e monocromatica su un FP.
Possiamo supporre che l'intensità del fascio sia così debole che un solo fotone alla volta di energia
h ν attraversi il FP.
2
Sappiamo che il fascio emergente ha ridotto la sua intensità del fattore cos θ .
ci chiediamo cosa accade al singolo fotone? Esso si divide (per così dire) in due parti una delle quali
passa e l'altra no?.
La risposta è perfettamente in linea con la descrizione di Planck Einstein; la radiazione è
quantizzata e se la frequenza è ν essa è trasportata da granuli di entità h ν . Il passaggio nel
FP non altera ν .
Quindi l'unica spiegazione possibile è che alcuni fotoni passino e altri no a caso, in modo che la
2
probabilità che essi attraversino il FP sia cos θ . Poiché dal punto di vista della meccanica
quantistica MQ l'intensità di un fascio è I =N h ν , ove N è il numero dei fotoni che attraversano
in un'unità di tempo un'unità di superficie perpendicolare al fascio, questo equivale a dire che una
2
frazione N cos θ è rivelata oltre il FP.
L'esperimento dice che in un test di superamento di un FP posto verticalmente tutti i fotoni
polarizzati V passano , nessun fotone polarizzato O passa e che in media uno su due passa se
polarizzato a 45°
É di fondamentale importanza sottolineare che questo è precisamente il significato di ciò che
dobbiamo intendere con “il fotone attraversa il FP” : e cioè che un opportuno rivelatore posto oltre
il FP fa “clic” quando è colpito dal fotone.
E altrettanto fondamentale sottolineare il fatto che il fatto che i fotoni superano a caso un test a 45°.
Questo è uno degli aspetti più rilevanti della teoria della MQ è cioè il carattere completamente
aleatorio dei processi microscopici
Non esiste nulla che differenzi un fotone dall'altro e che possa permetterci di prevedere se esso sia
rivelato oppure no oltre il FP.
sulla natura casuale dei processi fisici:
Meccanica classica : determinismo
Se conosco le leggi e tutte le condizioni al contorno ( posizioni e velocità di tutte le particelle) posso
determinare perfettamente tutti gli stati passati e futuri del sistema. E' solo l'incertezza delle misure
o la complessità del sistema che introduce la probabilità come descrizione necessaria, ma in linea di
principio eludibile
Meccanica quantistica
Le probabilità quantistiche non sono dovute a ignoranza o mancanza di informazioni o a
complessità del sistema: sono tutto ciò che posso affermare: l'aleatorietà e irriducibile.
Naturalmente esistono stati certi (probabilità =1) o impossibili (probabilità =0) .
La struttura probabilistica è incorporata nel formalismo.
La descrizione probabilistica non è legata a mancanza di informazioni.
Nel caso dei CBR la descrizione quantistica è la stessa: in un fascio polarizzato che forma un
angolo qualsiasi col cristallo alcuni fotoni verranno rivelati da un rivelatore posto all'uscita del
raggio O e altri su quello posto davanti al raggio S in accordo con Malus. Anche qui non è
possibile prevedere quali fotoni saranno rivelati su O o su S .
Interferenza e diffrazione di fotoni
si invia un un fotone alla volta su una singola fenditura oltre la quale viene posto o uno schermo
sensibile alla luce o un rivelatore. Cosa osservo?
La figura a campana descritta prima? Nulla di tutto ciò. Il fotone colpirà lo schermo in un punto
preciso e imprevedibile.
Un fotone dopo si formerà la figura di diffrazione , che risulterà quindi costruita con l'apporto di
un grande numero di fotoni.
Per l'interferenza sarà la stessa cosa. I fotoni si addensano nei punti più luminosi della figura di
interferenza e mai dove l'intensità e zero.
Domanda: come fa un fotone a sapere se l'altra fenditura e aperta o chiusa e quindi a costruire la
figura di interferenza o quella di diffrazione?
Particelle Materiali.
Nel 1924 il giovane fisico Luis De Broglie nella sua tesi di dottorato propose sulla base di
considerazione di simmetria che anche alle particelle materiali si dovesse dare un aspetto
h
ondulatorio con una lunghezza d'onda λ=
.
mv
h
In questo modo l'ipotesi di quantizzazione di Bohr e cioè mvr =n
e l'esistenza di orbite
2π
quantizzate sarebbe stata
spiegata immaginando l'elettrone
come un'onda stazionaria.
Infatti per avere un'onda
stazionaria su un'orbita di raggio
r deve essere 2 π r =n λ .
Utilizzando l'espressione
proposta da De Broglie si ottiene
Bohr.
Perché non abbiamo mai
osservato queste onde materiali?
A 300 K l'atomo di H ha una
−10
λ=10 m , che sono le
dimensioni di un atomo
Se De Broglie ha ragione allora devo poter osservare fenomeni di interferenza anche con elettroni.
Quelle in figura sono foto successive di una figura di interferenza di elettroni che va gradualmente
costruendosi. La sua idea è confermata dall'esperimento.
Basandosi sulle idee di De Broglie l'austriaco Erwin Schrodinger propose nel 1926 un modello
teorico basato su un'equazione d'onda che da lui prese il nome che segna la nascita alla cosiddetta
meccanica ondulatoria.
Contemporaneamente Heisenberg della scuola di Copenaghen e collaboratore di Bohr propose un
modello alternativo di meccanica quantistica basato sull'algebra delle matrici e fondato sull'analisi
delle grandezze osservabili e misurabili . Sempre Schrodinger dimostrò nel '26 l'equivalenza dei due
approcci.
Dualismo onda-corpuscolo
Unificazione di fenomeni così diversi
il fotone e le particelle elementari talvolta si comportano come onde talvolta come corpuscoli.
Nasce il problema di come interpretare e integrare aspetti all'apparenza contraddittori.
Questo problema è ancora aperto, nonostante gli innumerevoli successi e l'enorme capacità
predittiva che non ha eguali nella storia scientifica.
Una curiosità: nel 1937 G Thomson vinse il premio Nobel per aver dimostrato che l'elettrone è
un'onda. Suo padre 31 prima vinceva lo stesso premio per aver dimostrato l'elettrone è un
corpuscolo.
Esperimenti con elettroni
Figure di diffrazioni e interferenza con elettroni
Un fascio di particelle con velocità precise e quindi con λ precisa viene fatto passare in
opportune fenditure e poi rivelato al di là con un opportuno rivelatore.
Si fanno esperimenti con elettroni singolo al fine di evitare ogni interazione tra essi.
Domande : come fa l'elettrone a sapere se l'altra fenditura è aperta? Come fa ad interferire con se
stesso?
Lo Spin
Lo spin gioca per le particelle lo stesso ruolo che la polarizzazione ha per i fotoni.
Un sistema atomico possiede un momento angolare MA . Con ciò si intende che esiste un asse di
rotazione privilegiato attorno a cui l'elettrone “ruota” come una trottola.
Il MA è quantizzato sia in intensità che in direzione (rispetto ad una direzione fisicamente
caratterizzata, per es. un campo magnetico esterno).Le regole di quantizzazione dicono che i
possibili valori di L sono L=√ l (l + 1)ħ con ħ=
h
e l =0,1,2.. . Dato un valore di l
2π
esistono solo 2l +1 possibili orientazioni corrispondenti ai valori di m con −l ≤m≤l e
mħ è la proiezione di L lungo la direzione privilegiata .
Ad es. se l =2
L=√ 6 ħ e −2≤m ≤2 cioè m =−2,−1,0,1,2 -
lo spin o
momento angolare intrinseco cioè quello legato ad una rotazione su se stesso.
Fu ipotizzato nel 25 da Goudsmith e Uhlembeck per spiegare la struttura fine dello spettro
dell'atomo di H.. Ha analogie col MA orbitale ma con alcune importanti differenze.
1
3 3
S =√ s(s +1) E s=0, 1, 2,
…. .
2, 2, 2
Inoltre esso è una caratteristica intrinseca di ogni particella : per es per protoni, elettroni e neutroni
1
√3 ħ e m =−1 , 1 . Quindi rispetto ad una prefissata direzione lo spin
s=
per cui S =
2
2 2
2
1
1
ħ .
si può orientare solo in modo che rispetto “all'asse z” le proiezioni di S siano − ħ o
2
2
quindi in pratica spin su o spin giù. Lo spin non si allinea mai perfettamente con nessuna direzione.
Allo spin è associato un momento magnetico μ ( come un piccolo ago magnetico o una spira
percorsa da corrente: nell'ago μ è orientato dal polo Sud al polo Nord dell'ago).
I MA e gli spin si combinano vettorialmente con la regola del parallelogramma.
Esperimento di Stern e Gerlach (l'analogo
del cristallo birifrangente)
Nel '21 i due scienziati prendono un atomo
d'argento (che si scoprirà più tardi avere un
momento angolare totale= ( MA orbitale
totale + Spin totale) pari allo spin di un
singolo elettrone.
Sparano un e attraverso i poli di un magnete
opportunamente sagomati affinché il campo
sia crescente verso l'alto
(direzione z)
Lo spin particella può orientarsi rispetto a z
in su o in giù ;
in simboli usando una notazione dovuta a
Dirac |z −su ⟩ o |z −giuù⟩ .
|.... ⟩
un cosiddetto vettore ket definisce
un vettore di stato del sistema ovvero una
sua proprietà . Ad esempio |V ⟩
rappresenta un fotone con polarizzazione
verticale .
A S corrisponde μ , quindi a |z −su ⟩
corrisponde |μ−su ⟩ .
Il campo B agisce su entrambi i poli ma più
intensamente su polo N . di conseguenza la
particella devia verso l'alto .
Simmetricamente per |z −giuù⟩
per i fotoni a 45°
+
1
√2
|45 ⟩
=
1
√2
|V ⟩
|O ⟩
Consideriamo una particella avente lo spin orientato come l'asse x
1
1
1
1
|x−su ⟩= 2 |z su ⟩ + 2 |z−giuù⟩ e |x −giuù⟩= 2 |z su ⟩− 2 |z −giuù⟩
√
√
√
√
cosa accade a tale particella?
L'esperimento mostra che a caso metà devia verso su e metà verso giù.
Tale risultato è del tutto inspiegabile classicamente: nell'ambito di questa teoria l'ago può assumere
qualunque angolazione e pertanto dovrebbe essere deviato in modo continuo e colpire tutti i punti
tra S e G.
Principio di Heisenberg
Supponiamo di lanciare un fascio di fotoni o elettroni contro una fenditura .
Preparo un fascio di diametro D >> d ( dimensione della fenditura con velocità v ( v non ha
una componente perpendicolare allo schermo
L'incertezza con cui conosco la posizione prima della fenditura è D.
I fotoni che colpiscono lo schermo vengono confinati in un intervallo di posizioni d<<D , ma poiché
la figura di diffrazione è costituita da elettroni che colpiscono lo schermo costruendo la figura a
campana essi devono acquisire una componente di velocità parallela ( v x ) allo schermo.
. Nella diffrazione il I° minimo è corrisponde ad una deviazione angolare θ in modo che
d sin θ=λ . se d diminuisce θ aumenta e la campana si allarga.; ma questo significa che il
ventaglio di possibili valori di v x aumenta, cioè perdo informazione sulla velocità.
L'incertezza sulla posizione è Δ x=d .
h
h
¿ , da cui Δ x Δ v X ≥
Dalle leggi della diffrazione Δ v x ≥
m
md
. Il tentativo di conoscere più accuratamente la posizione (rimpicciolendo d) fa aumentare
l'incertezza sulla velocità ( e viceversa)
Esiste quindi un limite invalicabile e intrinseco alla possibilità di misurare qualsivoglia coppia di
grandezze i incompatibili (posizione e velocità, energia e tempo, …..)
Illustriamo più in profondità tale argomento. In astratto lo stato della particella al tempo t è
caratterizzato da un'ente matematico , il vettore di stato che lo specifica perfettamente. Esso può
essere rappresentato come |Ψ ,t ⟩ . Se siamo interessati alla posizione della particella posso
descrivere lo stato del sistema in modo del tutto equivalente per mezzo di una funzione d'onda
Ψ(r , t ) . per semplicità supponiamo che la particella sia vincolata a muoversi sull'asse x ,
cosicché essa assume la forma Ψ(x ,t ) . Questa funzione a valori complessi, , soluzione
dell'equazione di Schrodinger (nell'interpretazione della scuola di Copenaghen) gioca per le
particelle lo stesso ruolo del campo E per i fotoni. Vale a dire essa ha il ruolo di di ampiezza di
2
*
probabilità e il suo modulo quadro |Ψ (x , t ) |=Ψ Ψ rappresenta la densità di probabilità di
trovare la particella nel punto x.
In particolare l'area ombreggiata sotto la curva rappresenta la probabilità che la particella si trovi
nell'intervallo (a,b) . Si noti che l'area sotto l'intera curva deve valere uno perché la particella deve
sicuramente essere trovata da qualche parte. La Ψ ci da informazioni probabilistiche su tutte le
misure che vogliamo fare sul sistema. In particolare è possibile ricavare un a funzione Φ(v ,t )
che ci da attraverso il suo modulo quadro la probabilità che la particella abbia una certa velocità .
L'area ombreggiata della curva a destra ci da la probabilità che la velocità stia nell'intervallo (v,w).
E' possibile dimostrare che tanto più una delle due curve è “stretta” tanto (e più l'alta si allarga .
Il
Principio di Complementarietà (Bohr)
Bohr fa notare che i procedimenti sperimentali che mettono in evidenza gli aspetti corpuscolari e
quelli ondulatori sono impossibili da realizzare simultaneamente , come pure quelli che vogliono
definire i valori simultanei di coppie di grandezze incompatibili con qualsivoglia precisione.
Gli esperimenti mostrano l'evidenza di una doppia natura a livello di comportamento , ma mai
contemporaneamente.
Ad es se voglio sapere attraverso quale fenditura è passato l'elettrone distruggo la figura di
interferenza.
Il principio di sovrapposizione
Gli aspetti più sorprendenti della nuova teoria si rivelano quando essa si confronta con aspetti e
proprietà a noi familiari,sulle quali abbiamo radicate convinzioni; ad esempio sulla posizione.
E' importante sapere che gli esperimenti descritti sono stati effettivamente realizzati.
Inviamo un fotone su un cristallo birifrangente. Al di la del CBR è posto , in corrispondenza dei
cammini O e S un rivelatore.
Ia serie di esperimenti
•
•
•
•
•
i fotoni incidenti hanno polarizzazione verticale |V ⟩ . il rivelatore O registra il 100% dei
fotoni incidenti (ovvero la probabilità che il fotone sia rivelato è uno)
i fotoni incidenti hanno polarizzazione orizzontale |O ⟩ . il rivelatore S registra il 100%
dei fotoni incidenti (ovvero la probabilità che il fotone sia rivelato è uno).
Un FP posto all'uscita del CBR mostra che i fotoni nei due casi mantengono il loro stato di
polarizzazione
i fotoni incidenti hanno polarizzazione a 45° |45 ⟩ . il rivelatore O registra il 50% dei
fotoni incidenti e il rivelatore S altrettanto (a caso)
•
IIa serie di esperimenti
i fotoni in ingresso sono polarizzati a 45°
uno schermo viene posto alternativamente sui percorsi dei raggi O ,S e su entrambi tra il CBR e il
rivelatore
•
•
•
lo schermo è posto sul raggio O . Il totale dei fotoni che arriva è il 50% di quelli incidenti .
0% dei fotoni vengono registrati dal rivelatore O , il 100% di quelli che arriva (cioè il 50 %
del totale) è registrato da S . Un FP posto sul cammino mostra che i fotoni rivelati sono
polarizzati |O ⟩
lo schermo è posto sul raggio S. vale lo schema precedente .
Schermo su entrambi i raggi : nessun fotone viene rivelato.
IIIa serie di esperimenti
dopo il primo CBR ne viene posto uno al contrario che ricongiunge i cammini . Il secondo CBR
“disfa” ciò che ha fatto il primo
•
•
•
•
fotone incidente polarizzato verticalmente : il contatore registra 100% dei fotoni
fotoni incidente polarizzato orizzontalmente : il contatore registra il 100 % dei fotoni.
Un FP opportunamente posto tra il secondo CBR e il rilevatore mostra che la polarizzazione
è conservata.
Domanda da un milione di dollari : fotone incidente a 45° . Tra il secondo CBR e il
rivelatore viene posto un FP a 45*. cosa misura il rivelatore?
Analizziamo la situazione. Abbiamo visto che a caso 50% dei fotoni prendono il cammino O e 50 %
percorrono il cammino S mantenendo la polarizzazione. In un test di polarizzazione a 45°
attraverso un FP è stato in precedenza dimostrato che metà dei fotoni passa. Quindi metà dei fotoni
con stato |V ⟩ e metà di quelli con stato |O ⟩ passa. Quindi la metà del 50% + la metà
dell'altro 50 % fa un totale del 50%.
La previsione è che passi la metà dei fotoni passi (o ciò che è lo stesso la probabilità di essere
rivelato sia un mezzo).
L'esperimento realizzato molteplici attrezzature e su differenti particelle (oltre che con i fotoni)
smentisce completamente la nostra previsione: tutti i fotoni (100%) passano e il rivelatore fa clic
per ogni fotone in ingresso.
Questo fatto sorprendente diventa paradossale se ragioniamo sui percorsi dei fotoni:
Chiediamoci: quale strada ha percorso il fotone?
• Il cammino O ? La risposta è sicuramente NO perché abbiamo dimostrato con gli
esperimenti precedenti (con cammini schermati) che se un fotone percorresse tale cammino
verrebbe misurato in uscita il 50% dei fotoni in ingresso.
• Il cammino S ? sicuramente no per la stessa ragione.
• Entrambi i cammini? Sicuramente NO. In tutti gli esperimenti fatti per determinare il
percorso si trova sempre o un fotone intero o nessuno. Non è mai stato osservato mezzo
fotone su ciascuno dei due cammini.
• Nessuno dei due?. Il fotone potrebbe aver percorso altri cammini Sicuramente NO. Lo
dimostra l'esperimento con i due cammini schermati. In quel caso nessun fotone arriva.
Vale la pena di riflettere sul fatto che i quattro possibili cammini esauriscono le possibilità logiche.
Da dove nasce questo paradosso? Dal fatto che noi abbiamo attribuito ai fotoni (e alle altre
particelle elementari) proprietà e caratteristiche che valgono nel mondo macroscopico, ma sono
prive di senso nel mondo dell'infinitamente piccolo. Il fatto è che noi abbiamo tacitamente assunto
che i fotoni avessero un preciso stato prima dell'impatto col rilevatore, ovvero come logicamente
equivalenti le affermazioni: “il rivelatore O registra on fotone nel momento in cui esso lo colpisce”
con “ il fotone prima dell'impatto era nello stato che corrisponde alla sua propagazione lungo il
cammino O .
La MQ descrive questo peculiare modo di essere dei fotoni e delle altre particelle come
“sovrapposizione “. Il fotone quindi prima della misura è nella sovrapposizione |V ⟩ +|O ⟩ che
evidentemente, per l'analisi fatta, è logicamente diverso da essere sul cammino O, o sul cammino
S, su entrambi o su nessuno dei due.
Per approfondire ulteriormente questo punto analizziamo la situazione all'uscita del primo CBR,
utilizzando il linguaggio della funzione d'onda. Rappresentiamo la situazione come in figura ,
I cammini sono stati sostituiti da strisce di un certo spessore . Le due regioni ombreggiate
all'uscita del cristallo rappresentano le due regioni dove la funzione d'onda è diversa da 0. Il +
indica proprio lo stato di sovrapposizione. Tenuto conto del significato probabilistico della funzione
d'onda analizziamo le situazioni corrispondenti al caso dei fotoni polarizzati |V ⟩ , |O ⟩ e
|45. ⟩
.
Nel primo caso la funzione d'onda è diversa da 0 solo sul raggio O. l'area sotto il rettangolo vale
uno; il che significa che in una misura di posizione si ha probabilità uno di trovare il fotone in
quella posizione. Analogamente per il raggio S. Per il fotone a 45° invece la probabilità di trovarlo
1
1
1
nella posizione O (S) è
. Dalle formule analizzate all'inizio |Ψ ⟩= |V ⟩ + |O ⟩ .
2
√2
√2
La probabilità di trovare il fotone in O o in S è comunque uguale a uno . Ma ricombinando i fasci si
ha interferenza delle due onde e questo impedisce di affermare che il fotone era sul percorso O
oppure S anche prima della misura.
Ragionamenti del tutto analoghi possono essere fatti per analizzare l'interferenza di fotoni o
elettroni da due fenditure.
Un altro dispositivo
Uno specchio semi-argentato SA è uno specchio in cui parte della luce che lo colpisce viene
riflessa, parte viene trasmessa. Si può dimostrare che Il raggio riflesso ritarda di un quarto di
lunghezza d'onda rispetto a quello trasmesso e che la polarizzazione della radiazione è
completamente ininfluente.
Ragioniamo ancora in termini di fotoni. Un fotone incide su SA inclinato a 45° . Oltre lo specchio
sono posti due rivelatori , uno in corrispondenza della direzione non deviata, l'altro a 90° rispetto a
questa (l'angolo di incidenza è uguale a quello di riflessione, quindi 45°+45°=90°).
Anche in questo esperimento 50%dei fotoni colpisce il rivelatore X, 50% quello Y . Anche in questo
caso è impossibile prevedere l'esito singolo. Utilizzando il linguaggio della funzione d'onda
dovremo anche qui scrivere che prima che uno dei due contatori scatti il fotone si trova nella
1
1
sovrapposizione |Ψ ⟩= |X ⟩ + |Y ⟩ e che solo la misura farà “collassare la funzione d'onda in
√2
√2
un preciso stato. Gli stessi ragionamenti di prima renderanno illegittimo affermare che il fotone sta
su x, o y o su entrambi o su nessuno.
Dopo questa premessa introduciamo un apparato sperimentale come quello in figura
I raggi uscenti da SA1 vengono deviati da due specchi (normali) S1 e S2 e ridiretti verso un
secondo specchi semi-argentato SA2 oltre il quale, in direzioni perpendicolari, vengono posti due
rivelatori.
I raggi che colpiscono il rivelatore V subiscono ciascuno sui rispettivi percorsi due riflessioni e
pertanto sono in fase, quelli che colpiscono il contatore W subiscono rispettivamente una
riflessione (quello che prosegue indisturbato dopo SA1) e tre riflessioni l'altro. Pertanto esso è
sfasato di mezza lunghezza d'onda rispetto al primo.
Nel primo caso quindi i raggi interferiscono costruttivamente nel secondo caso l'interferenza è
distruttiva. Poiché il quadrato del campo regola la probabilità di rivelare il fotone se si esegue una
misura di posizione, allora nel modello dei fotoni il 100% di essi viene rivelato da V e nessuno da
W
Notiamo che se togliamo SA2 i raggi proseguiranno indisturbati e in media i contatori V e W
registreranno ciascuno metà dei fotoni.
Supponiamo però ora che lo strumento sia gigantesco e che i tratti dopo SA1 siano cosi lunghi da
permettere di avere il tempo di togliere o inserire SA2 in maniera del tutto casuale. Mandiamo un
fotone nell'apparecchio e dopo che esso ha attraversato SA1 o è stato riflesso verso S2 , decidiamo,
a caso, di lasciare oppure rimuovere SA2.
In base alla discussione precedente la presenza o l'assenza di SA2 cambia radicalmente il risultato
della misura: se lo specchio è al suo posto il fotone deve inevitabilmente essere rivelato da V, nel
caso contrario ha la stessa probabilità di essere rivelato da V o W.
Ora consideriamo il fotone in arrivo quando SA2 è inserito: esso non può essere rivelato da W a
causa dell'interferenza. Se invece lo specchi SA2 non è inserito il fotone per attivare W deve il aver
percorso il tratto SA1 -S1. Ma la scelta di mettere o togliere SA2 è stata fatta dopo che il fotone ha
attraversato SA1; quindi esso ha già scelto se percorrere “due cammini o uno soltanto”. Tale scelta
ha quindi paradossalmente un effetto retroattivo sul comportamento del fotone.
Effetto tunnel
Supponiamo che una pallina si diriga contro una rampa di altezza h. Classicamente essa potrà
superare oltrepassare la rampa solo se la sua energia cinetica all'inizio della rampa è maggiore o
uguale a mgh. In caso contrari si fermerà prima della sommità e ricadrà all'indietro. In questo senso
la rampa rappresenta una barriera fisica che corrisponde ad una barriera di potenziale ( o di energia
potenziale). In MQ , invece la probabilità di superare la barriera in queste condizioni non è nulla..
Per un'opportuna scelta di altezza e ampiezza della barriera un elettrone per esempio può avere un a
probabilità pari al 50% di essere rivelato oltre la barriera. Tale effetto si chiama effetto tunnel ed è
di fondamentale importanza nella descrizione di alcuni processi nucleari come per esempio la
radioattività












