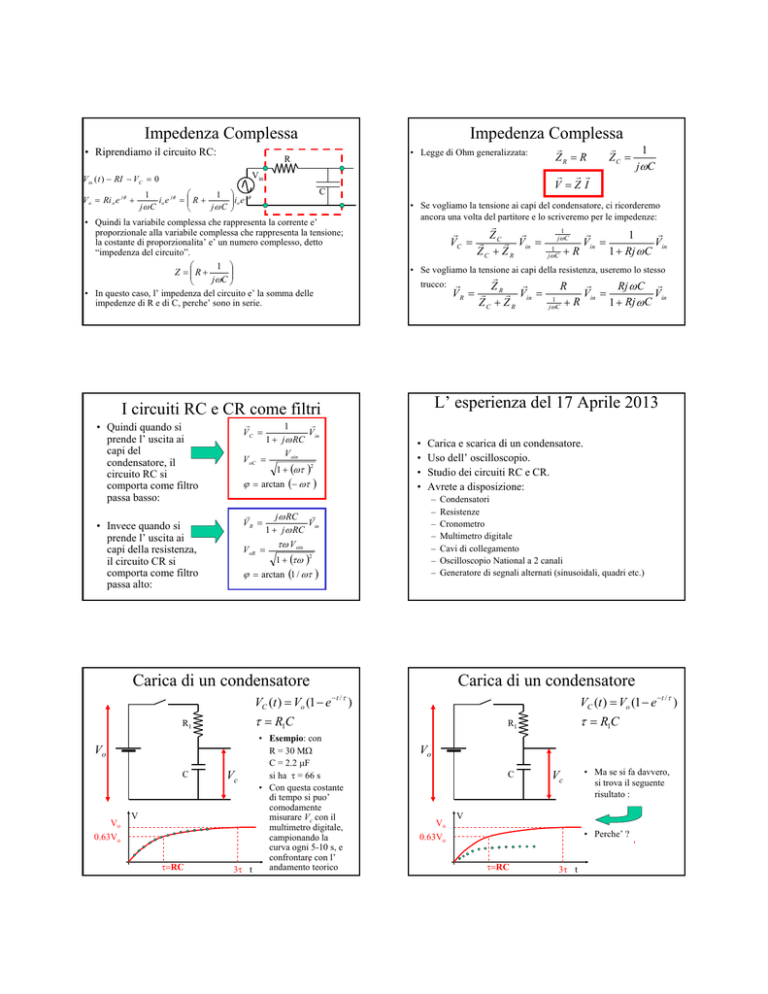
Impedenza Complessa
• Riprendiamo il circuito RC:
R
⎛
1
1
io e j φ = ⎜⎜ R +
jω C
jω C
⎝
⎞ jφ
⎟⎟ io e
⎠
C
r
r
r
ZC
r
r Vin =
VC =
ZC + Z R
trucco:
C
Vo
V
0.63Vo
τ=RC
jω C
+R
r
Vin =
r
1
Vin
1 + Rj ω C
r
r
r
ZR
r Vin =
VR = r
ZC + Z R
r
R
Rj ω C r
Vin =
Vin
R
Rj ω C
+
1
+
jω C
1
r
VC =
V oC
r
1
V in
1 + j ω RC
V oin
=
2
1 + (ωτ )
ϕ = arctan (− ωτ
r
VR =
V oR =
•
•
•
•
)
1 + (τω
)2
ϕ = arctan (1 / ωτ
Carica e scarica di un condensatore.
Uso dell’ oscilloscopio.
Studio dei circuiti RC e CR.
Avrete a disposizione:
–
–
–
–
–
–
–
j ω RC r
V in
1 + j ω RC
τω V oin
)
VC (t ) = Vo (1 − e
Vo
1
L’ esperienza del 17 Aprile 2013
Condensatori
Resistenze
Cronometro
Multimetro digitale
Cavi di collegamento
Oscilloscopio National a 2 canali
Generatore di segnali alternati (sinusoidali, quadri etc.)
Carica di un condensatore
R1
1
jω C
• Se vogliamo la tensione ai capi della resistenza, useremo lo stesso
I circuiti RC e CR come filtri
• Invece quando si
prende l’ uscita ai
capi della resistenza,
il circuito CR si
comporta come filtro
passa alto:
r
1
ZC =
jωC
• Se vogliamo la tensione ai capi del condensatore, ci ricorderemo
ancora una volta del partitore e lo scriveremo per le impedenze:
• Quindi la variabile complessa che rappresenta la corrente e’
proporzionale alla variabile complessa che rappresenta la tensione;
la costante di proporzionalita’ e’ un numero complesso, detto
“impedenza del circuito”.
⎛
1 ⎞
⎟
Z = ⎜⎜ R +
jωC ⎟⎠
⎝
• In questo caso, l’ impedenza del circuito e’ la somma delle
impedenze di R e di C, perche’ sono in serie.
• Quindi quando si
prende l’ uscita ai
capi del
condensatore, il
circuito RC si
comporta come filtro
passa basso:
r
ZR = R
r rr
V =Z I
Vin
V in ( t ) − RI − V C = 0
V o = Ri o e j φ +
Impedenza Complessa
• Legge di Ohm generalizzata:
Carica di un condensatore
−t /τ
VC (t ) = Vo (1 − e −t / τ )
)
τ = R1C
• Esempio: con
R = 30 MΩ
C = 2.2 μF
si ha τ = 66 s
Vc
• Con questa costante
di tempo si puo’
comodamente
misurare Vc con il
multimetro digitale,
campionando la
curva ogni 5-10 s, e
confrontare con l’
andamento teorico
3τ t
τ = R1C
R1
Vo
C
Vo
Vc
• Ma se si fa davvero,
si trova il seguente
risultato :
V
• Perche’ ?
0.63Vo
τ=RC
3τ t
Carica di un condensatore
Carica di un condensatore
VC (t ) = Vo (1 − e
−t /τ
VC (t ) = Vo (1 − e −t / τ )
)
τ = R1C
R1
τ = R1C
R1
Vo
Vo
C
Vo
• Ma se si fa davvero,
si trova il seguente
risultato :
Vc
C
• Siccome nel
multimetro, usato
come voltmetro,
R2
scorre una piccola
corrente, esso e’
equivalente ad una
resistenza R2 posta
in parallelo al
condensatore.
• La soluzione Vc(t)
non vale piu’.
Vc
V
0.63Vo
τ=RC
3τ t
• Perche’ ?
• Il multimetro
perturba la misura !
Carica di un condensatore
⎧Vo = VC + R1i1
⎪ V =Ri
2 2
⎪ C
⎨
Q
=
V
⎪ C C
⎪ i =i +i
⎩ 1 2 C
⎧Vo = VC + R1i1
⎪ V =Ri
2 2
⎪ C
⎨ dV C iC
=
⎪
dt
C
⎪ i =i +i
⎩ 1 2 C
R1
Carica di un condensatore
i1
Vo
i2
C
iC
R2
Vc
dV C
1
V
VC = o
+
dt
CR P
CR1
dV C 1 ⎛ 1
1 ⎞
V
⎟VC = o
+ ⎜⎜ +
dt
C ⎝ R1 R2 ⎟⎠
CR1
Carica di un condensatore
R1
=
C
Vc
R2
R1
R1
Vo
=
Vo
R2
Per il Teorema di
Thevenin, il circuito
riquadrato e’ equivalente
ad un generatore ideale di
tensione con in serie una
resistenza.
i1
Vo
i2
C
iC
R2
Vc
Ma c’e’ un metodo molto
piu’ semplice !
dV C
1
V
VC = o
+
dt
CR P
CR1
Carica di un condensatore
R1
Vo
⎧Vo = VC + R1i1
⎪ V =Ri
2 2
⎪ C
⎨ dV C iC
=
⎪
C
dt
⎪ i =i +i
⎩ 1 2 C
dV C i2 − i1 1 V o − VC 1 VC
=
=
−
dt
C
C
R1
C R2
dV C i1 − i2
1 V o − VC 1 VC
=
=
−
dt
C
C R1
C R2
dV C 1 ⎛ 1
1 ⎞
V
⎟VC = o
+ ⎜⎜ +
dt
C ⎝ R1 R2 ⎟⎠
CR1
⎧Vo = VC + R1i1
⎪ V =Ri
2 2
⎪ C
Q
⎨
V
=
⎪ C C
⎪ i =i +i
⎩ 1 2 C
C
Vc
R2
RE
VE
C
C
Vc
Per il Teorema di
Thevenin, il circuito
riquadrato e’ equivalente
ad un generatore ideale di
tensione con in serie una
resistenza con:
Vc
RE =
R1 R 2
R1 + R 2
V E = Vo
R2
R1 + R 2
Carica di un condensatore
RE =
RE
VE = Vo
VE
R2
R1 + R2
Vc
V C (t ) = V o
τ = RE C
τ =
Vo
• Circuito da studiare:
• Ci interessa studiare Vout
(segnale in uscita) al variare di
Vin (segnale in ingresso).
• Ad esempio se Vin e’
sinusoidale, Vout sara’ anch’esso
sinusoidale, con la stessa
frequenza ma con ampiezza e
fase date dalle relazioni
-1
(Vo-Vc)/Vo
10
Vc/Vo
-2
10
0.2
r
VR =
-3
10
0.1
0.0
V oR =
-4
0
200
400
t(s)
600
800
1000
10
0
100
R2
R1 + R 2
τ=RC
0
0.3
V
Vo
Vo
10
0.4
Vc
R2
(1 − e − t / τ )
R1 + R 2
Pendenza = -1/RPC
R1=30 MΩ
R2=10MΩ
C=2.2 μF
R1 R 2
C
R1 + R 2
τ =
C
R2
R1 R 2
C
R1 + R 2
0.5
R2
(1 − e − t / τ )
R1 + R 2
V C (t ) = V o
R1
Ma ora il circuito e’ proprio
uguale al circuito ideale della
carica di un condensatore, del
quale abbiamo gia’ la
soluzione:
C
VC (t ) = VE (1 − e − t / τ )
Carica di un condensatore
R1 R2
R1 + R2
200
300
t (s)
400
500
r
j ω RC
V in
1 + j ω RC
τω V oin
1 + (τω
)
3τ t
Misure sul
circuito CR
C
Vin
R
Vout
2
ϕ = arctan (1 / ωτ
)
• E quindi ci interessa costruire
una tabella di VoRt/Voin e φ in
funzione di f=ω/2π.
• In pratica: si monta il
circuito CR sulla
basetta e si collega al
generatore di Vin ed ai
due canali dell’
oscilloscopio per
misurare sia Vin (su
CH1) che Vout (su
CH2).
Misure sul circuito CR
C
GEN
CH1
• Problemi pratici:
• Le connessioni ai
BNC vanno fatte
con cavetti
BNC-coccodrillo. Il
rosso e’ connesso al
centrale, il nero allo
schermo.
Misure sul circuito CR
C
GEN
CH1
CH2
CH2
R
Generatore
di segnali
Basetta
R
Oscilloscopio
Generatore
di segnali
Basetta
Oscilloscopio
• Problemi pratici:
• Le connessioni ai
BNC vanno fatte
con cavetti
BNC-coccodrillo.
Il rosso e’
connesso al
centrale, il nero
allo schermo.
CH1
CH2
Oscilloscopio
C
GEN
R
Generatore
di segnali
VoC
Vo
Misure sul circuito CR
Circuito RC: Filtro passa basso:
r
VC =
Vo / 2
0
Oscilloscopio
Basetta
0
1
2
3
4
5
6
0 0
1
2
3
4
5
6
φ
ωRC
V oC
−π/4
−π/2
ωRC
r
1
V in
1 + j ω RC
V oin
=
2
1 + (ωτ )
ϕ = arctan (− ωτ
r
VR =
0
π/2
π/4
)
Circuito CR: Filtro passa alto :
Vo
0
φ
0 0
1
1
2
2
3
3
4
4
5
5
6
6
ωRC
ωRC
V oR =
j ω RC r
V in
1 + j ω RC
τω V oin
1 + (τω
)2
ϕ = arctan (1 / ωτ
)
Misure da fare:
• Per ciascun circuito (sia CR che RC):
• Visualizzando Vout e Vin in funzione del tempo (ricordarsi
di azzerare le due tracce sulla meta’ dello schermo mettendo
a GND i due ingressi) si costruisce una tabella di f, Vout, Vin,
Δt. Da queste misure si ricavano le altre due colonne per
A(f)= Vout/Vin e Δφ(f)=2π Δt/T che vanno graficate.
Vin
• La connessione tra
Misure sul circuito CR
la GND del CH1 e
la GND del CH2
(cioe’ tra gli schermi
dei connettori BNC
di ingresso) e’ gia’
C
presente all’ interno
GEN
CH1
dell’ oscilloscopio.
CH2
• Ci si deve ricordare
di questo quando si
R
costruisce un
qualsiasi circuito: la
connessione di GND
deve essere fatta
sempre con questo Generatore Basetta
Oscilloscopio
punto.
di segnali
Vout
• La prima cosa da fare e’ stimare fo dai valori di R e C.
Consiglio una frequenza di taglio (il generatore lavora in
frequenza f) fo=ωo/2π dell’ ordine di 1000 Hz o piu’.
• Qui ωo e’ tale da rendere la risposta Vout/Vin=1/sqrt(2),
quindi ωo=1/τ=1/RC e fo=1/(2πRC)
• Esempio: R=10kΩ, C=10nF, fo=1.6kHz
• Si deve poi fare una scansione veloce da 0.1fo a 10fo , in
modo da vedere se c’e’ davvero un taglio (passa alto o
passa basso rispettivamente) nell’ ampiezza del segnale di
uscita (quella d’ ingresso deve rimanere costante).
• Se non c’e’, il circuito non e’ stato montato bene, e quindi
non si deve cominciare a fare le misure !
• Se succede quello che ci si aspetta, si procede alle misure.
• Visualizzando Vout in funzione di Vin (ricordarsi di centrare il
puntino luminoso mettendo a GND i due ingressi all’ inizio) si
costruisce una tabella di f, a, b. Si ricava poi sinΔφ(f)=a/b=c/d e si
grafica.
b
a
c
t
d
Δt
• Dai grafici si ricava il valore della frequenza di taglio.
sinΔφ(f)=a/b=c/d












