3 LICEO SCIENTIFICO (OPZIONE

LICEO STATALE "DON. G. FOGAZZARO"
Anno sc. 2016 -2017
DISCIPLINA: MATEMATICA
CLASSE: 3 LICEO SCIENTIFICO (OPZIONE SCIENZE APPLICATE)
OBIETTIVI SPECIFICI DI APPRENDIMENTO
Con riferimento al profilo educativo, culturale e professionale dello studente liceale e alle indicazioni nazionali, riguardanti gli
obiettivi specifici di apprendimento concernenti le attività e gli insegnamenti compresi nei piani degli studi previsti per i percorsi
liceali, il percorso didattico dovrà far acquisire allo studente le seguenti conoscenze ed abilità:
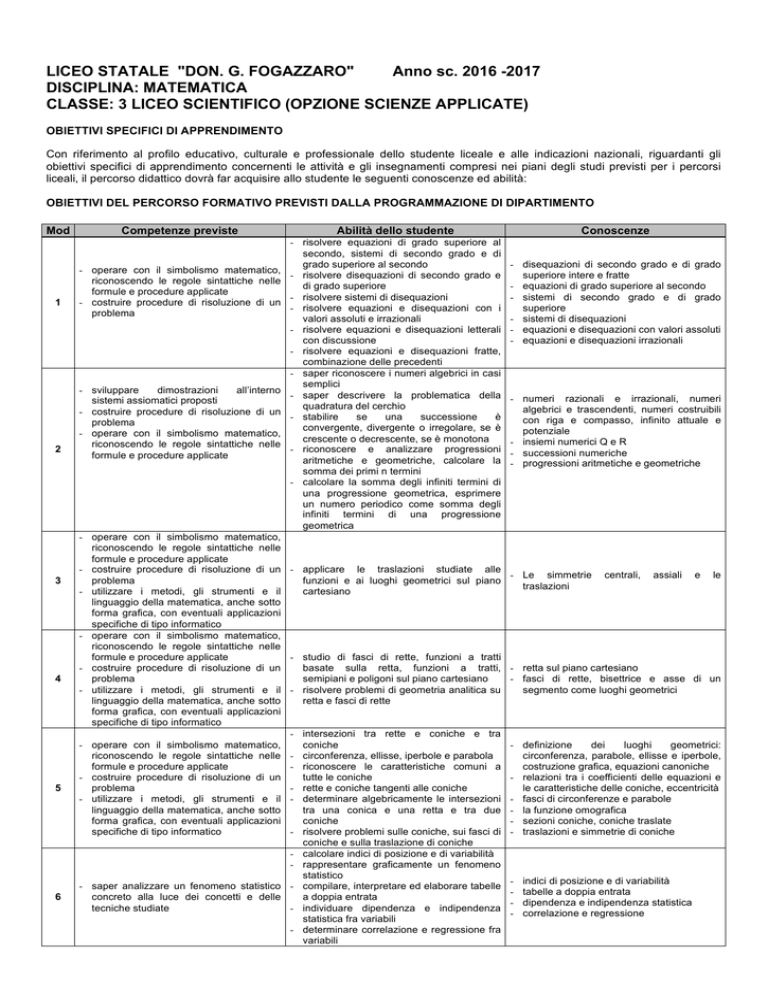
OBIETTIVI DEL PERCORSO FORMATIVO PREVISTI DALLA PROGRAMMAZIONE DI DIPARTIMENTO
Mod
1
2
3
4
5
6
Competenze previste
- operare con il simbolismo matematico,
riconoscendo le regole sintattiche nelle
formule e procedure applicate
- costruire procedure di risoluzione di un
problema
- sviluppare
dimostrazioni
all’interno
sistemi assiomatici proposti
- costruire procedure di risoluzione di un
problema
- operare con il simbolismo matematico,
riconoscendo le regole sintattiche nelle
formule e procedure applicate
Abilità dello studente
- risolvere equazioni di grado superiore al
secondo, sistemi di secondo grado e di
grado superiore al secondo
- risolvere disequazioni di secondo grado e
di grado superiore
- risolvere sistemi di disequazioni
- risolvere equazioni e disequazioni con i
valori assoluti e irrazionali
- risolvere equazioni e disequazioni letterali
con discussione
- risolvere equazioni e disequazioni fratte,
combinazione delle precedenti
- saper riconoscere i numeri algebrici in casi
semplici
- saper descrivere la problematica della
quadratura del cerchio
- stabilire
se
una
successione
è
convergente, divergente o irregolare, se è
crescente o decrescente, se è monotona
- riconoscere e analizzare progressioni
aritmetiche e geometriche, calcolare la
somma dei primi n termini
- calcolare la somma degli infiniti termini di
una progressione geometrica, esprimere
un numero periodico come somma degli
infiniti termini di una progressione
geometrica
- operare con il simbolismo matematico,
riconoscendo le regole sintattiche nelle
formule e procedure applicate
- costruire procedure di risoluzione di un - applicare le traslazioni studiate alle
problema
funzioni e ai luoghi geometrici sul piano
- utilizzare i metodi, gli strumenti e il
cartesiano
linguaggio della matematica, anche sotto
forma grafica, con eventuali applicazioni
specifiche di tipo informatico
- operare con il simbolismo matematico,
riconoscendo le regole sintattiche nelle
formule e procedure applicate
- studio di fasci di rette, funzioni a tratti
- costruire procedure di risoluzione di un
basate sulla retta, funzioni a tratti,
problema
semipiani e poligoni sul piano cartesiano
- utilizzare i metodi, gli strumenti e il - risolvere problemi di geometria analitica su
linguaggio della matematica, anche sotto
retta e fasci di rette
forma grafica, con eventuali applicazioni
specifiche di tipo informatico
- intersezioni tra rette e coniche e tra
- operare con il simbolismo matematico,
coniche
riconoscendo le regole sintattiche nelle - circonferenza, ellisse, iperbole e parabola
formule e procedure applicate
- riconoscere le caratteristiche comuni a
- costruire procedure di risoluzione di un
tutte le coniche
problema
- rette e coniche tangenti alle coniche
- utilizzare i metodi, gli strumenti e il - determinare algebricamente le intersezioni
linguaggio della matematica, anche sotto
tra una conica e una retta e tra due
forma grafica, con eventuali applicazioni
coniche
specifiche di tipo informatico
- risolvere problemi sulle coniche, sui fasci di
coniche e sulla traslazione di coniche
- calcolare indici di posizione e di variabilità
- rappresentare graficamente un fenomeno
statistico
- saper analizzare un fenomeno statistico - compilare, interpretare ed elaborare tabelle
concreto alla luce dei concetti e delle
a doppia entrata
tecniche studiate
- individuare dipendenza e indipendenza
statistica fra variabili
- determinare correlazione e regressione fra
variabili
Conoscenze
- disequazioni di secondo grado e di grado
superiore intere e fratte
- equazioni di grado superiore al secondo
- sistemi di secondo grado e di grado
superiore
- sistemi di disequazioni
- equazioni e disequazioni con valori assoluti
- equazioni e disequazioni irrazionali
- numeri razionali e irrazionali, numeri
algebrici e trascendenti, numeri costruibili
con riga e compasso, infinito attuale e
potenziale
- insiemi numerici Q e R
- successioni numeriche
- progressioni aritmetiche e geometriche
- Le simmetrie
traslazioni
centrali,
assiali
e
le
- retta sul piano cartesiano
- fasci di rette, bisettrice e asse di un
segmento come luoghi geometrici
- definizione
dei
luoghi
geometrici:
circonferenza, parabole, ellisse e iperbole,
costruzione grafica, equazioni canoniche
- relazioni tra i coefficienti delle equazioni e
le caratteristiche delle coniche, eccentricità
- fasci di circonferenze e parabole
- la funzione omografica
- sezioni coniche, coniche traslate
- traslazioni e simmetrie di coniche
-
indici di posizione e di variabilità
tabelle a doppia entrata
dipendenza e indipendenza statistica
correlazione e regressione
- Utilizzare metodi, strumenti e modelli
matematici in situazioni diverse
- Disegnare il grafico di una funzione
- Utilizzare
modelli
esponenziali
e
esponenziale o logaritmica
logaritmici attinenti a situazioni reali
- Risolvere
equazioni
e
disequazioni
- Operare con il simbolismo matematico
esponenziali e logaritmiche
riconoscendo le regole sintattiche di
trasformazione di formule
7
- Esponenziali e logaritmi
- Potenze ad esponente reale, la funzione
esponenziale
- Equazioni e disequazioni esponenziali
- Definizione di logaritmo, la funzione
logaritmo
- Proprietà dei logaritmi, cambiamento di
base
- Equazioni e disequazioni logaritmiche
SCANSIONE DI MASSIMA DEL PROGRAMMA CON INDICAZIONE DEL PERIODO DI SVOLGIMENTO:
Modulo
2
3
4
Periodo
Stima ore previste
Equazioni e disequazioni
Settembre/Ottobre
18
2
Numeri trascendenti, successioni e progressioni
Ottobre/Novembre
10
3
Trasformazioni sul piano cartesiano
Novembre
8
4
Complementi sulla retta nel piano cartesiano
Dicembre/Gennaio
18
5
Le coniche
Febbraio/marzo/aprile
48
6
Statistica
Aprile/maggio
12
7
Esponenziali e logaritmi
Maggio/giugno
18
Mod.
1
Argomento
1
Argomento
Equazioni e disequazioni
Contenuti
Obiettivi minimi
Le disequazioni intere di 2^ grado e di
grado superiore al 2^. Equazioni e
disequazioni irrazionali. Equazioni e
disequazioni
con
valori
assoluti.
Disequazioni
fratte.
Sistemi
di
disequazioni. Problemi risolvibili con
disequazioni.
• Risolvere disequazioni di secondo grado e di
grado superiore
• Risolvere sistemi di disequazioni
• Risolvere equazioni e disequazioni irrazionali
nei casi standard
• Risolvere semplici equazioni e disequazioni
con i valori assoluti
• Risolvere equazioni e disequazioni fratte,
combinazioni delle disequazioni precedenti
• Risolvere semplici problemi che hanno come
modello disequazioni.
• Conoscere i concetti di numero algebrico e
I numeri razionali e i numeri irrazionali. I trascendente, il problema della quadratura del
Numeri trascendenti,
numeri algebrici e i numeri trascendenti. cerchio, di cardinalità del numerabile e del
successioni e progressioni Successioni. Progressioni aritmetiche e continuo, di infinito attuale e potenziale
geometriche.
• Riconoscere ed effettuare semplici calcoli con
le progressioni aritmetiche e geometriche
Trasformazioni sul piano
cartesiano
Simmetrie centrali ed assiali. Traslazioni. • Saper applicare le trasformazioni studiate alle
Le trasformazioni e i grafici delle funzioni.
funzioni sul piano cartesiano.
Complementi sulla retta
nel piano cartesiano
Ripasso del piano cartesiano e degli
elementi principali dello studio della retta
sul piano cartesiano (forma implicita ed
esplicita, disegno di rette, equazione di
una retta passante per due punti, etc.). • Risolvere problemi di geometria analitica sulla
Funzioni lineari a tratti. Distanza punto- retta e sui fasci di rette
retta. Rette parallele e perpendicolari.
Bisettrici. Fasci di rette. Semipiani,
segmenti, semirette, angoli e poligoni nel
piano cartesiano.
5
Le coniche
6
Statistica
Circonferenza. Fasci di circonferenze. La
parabola. Fasci di parabole. L’ellisse.
Ellissi traslate. L’iperbole. Vari tipi di
iperbole. L’iperbole traslata. Coniche e
luoghi geometrici.
Introduzione
alla
statistica.
Indici
• Determinare l’equazione di una conica note
alcune condizioni
• Determinare le intersezioni tra una retta e una
conica e tra due coniche
• Determinare le rette tangenti alle coniche
• Risolvere semplici problemi di geometria
analitica con le coniche
• Operare traslazioni di coniche
• Riconoscere l’equazione di un’ellisse e di
un’iperbole non centrate nell’origine del
sistema di riferimento
di • Conoscere i concetti e saper calcolare le
posizione e di variabilità. Tabelle e variabili di base della statistica
indipendenza statistica. Correlazione e • Conoscere e saper calcolare gli indici di
regressione.
posizione e di variabilità
• Saper
rappresentare
graficamente
un
fenomeno statistico
• Saper compilare e interpretare tabelle a
doppia entrata
• Saper individuare e valutare relazioni di
dipendenza fra due variabili, correlazione e
regressione lineare
7
Esponenziali e logaritmi
Potenze ad esponente razionale. La
funzione esponenziale. Equazioni e
disequazioni esponenziali. La funzione
logaritmica.
proprietà
dei
logaritmi.
Equazioni logaritmiche ed equazioni
esponenziali risolvibili mediante logaritmi.
Disequazioni logaritmiche e disequazioni
esponenziali risolvibili mediante logaritmi.
Modelli di crescita e decadimento.
• Dominio
e
proprietà
delle
funzioni
esponenziale e logaritmica
• Disegnare
i
grafici
della
funzione
esponenziale e della funzione logaritmica
• Conoscere i teoremi sui logaritmi
• Saper risolvere semplici equazioni e
disequazioni esponenziali e logaritmiche
SPAZI
Oltre all’aula, dotata o meno di LIM, si potrà eventualmente fare uso, a seconda delle necessità, di altri spazi, come il laboratorio di
informatica, o visite didattiche.
METODI
•
•
Lezioni frontali. L’alunno acquisisce la capacità di ascoltare, comprendere e sintetizzare gli argomenti trattati in classe.
Problem solving. Nell’introdurre gli argomenti vengono proposti agli alunni situazioni di vita reale in cui sono necessari gli
strumenti matematici e/o le formule della fisica che devono essere trattate in quella lezione.
•
Esercitazioni. Gli studenti svolgono in classe gli esercizi proposti con l’aiuto dell’insegnante e con la collaborazione dei
compagni vicini.
•
Svolgimento di esercizi guidati. E’ previsto lo svolgimento di esercizi con la spiegazione puntuale dei passaggi e delle
regole teoriche utilizzate al fine di aiutare i ragazzi a sviluppare strategie risolutive.
•
Correzione degli esercizi per casa. I compiti assegnati vengono corretti in classe dall'insegnante o sotto la guida di
quest'ultimo dagli studenti che hanno incontrato difficoltà nel loro svolgimento.
MEZZI (MANUALI IN ADOZIONE, LIM, DISPENSE….)
Sarà utilizzato sistematicamente il libro di testo adottato, che consente una buona articolazione degli argomenti e una vasta scelta
di esercizi e problemi.
Saranno utilizzati inoltre
•
Strumenti multimediali (LIM, audiovisivi)
•
Appunti dell’insegnante
CRITERI DI VALUTAZIONE (GRIGLIE ED ALTRO)
Le prove di accertamento previste sono le seguenti:
Interrogazioni e/o prove strutturate e/o semistrutturate
verifiche scritte
In tutto almeno tre prove nel trimestre e quattro nel pentamestre
La correzione delle prove scritte (di qualunque tipo) verrà fatta in classe nei giorni successivi a quello dello svolgimento della prova,
che sarà consegnata agli studenti nel più breve tempo possibile, possibilmente mai oltre le due settimane successive allo
svolgimento della stessa. Gli studenti assenti in una giornata in cui si svolge una prova scritta recupereranno talvolta per iscritto,
con una prova analoga, talvolta con un’interrogazione, a seconda del numero degli studenti assenti e delle opportunità contingenti.
Per la valutazione il Dipartimento di matematica e fisica ha elaborato la griglia allegata.
CRITERI E MODALITA' DI RECUPERO
Le attività di recupero potranno essere attuate nelle seguenti possibili forme:
a) recupero curricolare con l’insegnante, a classe intera o per piccoli gruppi
b) sportello per gli studenti, con il proprio o altri insegnanti
c) corsi di recupero da effettuarsi in orario extrascolastico
d) corsi di recupero da effettuarsi durante il periodo estivo
Le modalità adottate dipenderanno dalle scelte dell’insegnante e dalle decisioni organizzative prese a livello di Istituto.
GRIGLIA DI VALUTAZIONE DI MATEMATICA E FISICA
CONOSCENZE
dei concetti
della terminologia
specifica
COMPETENZE
espositive
argomentative
ABILITA’
di calcolo
risolutive
Esposizione ed
argomentazioni assenti.
Svolgimento assente o diffusi e gravi
errori in operazioni elementari.
Esposizione ed
argomentazioni confuse o
non pertinenti.
Diffusi e gravi errori.
VOTO/1
0
Rifiuto di rispondere alle domande.
Conoscenze assenti.
Gravi incomprensioni concettuali.
Mancato uso della terminologia
specifica.
Conoscenze non pertinenti.
Gravi incomprensioni concettuali.
Uso della terminologia specifica
errato o confuso.
Conoscenze incomplete,
superficiali e non organiche.
Esposizione poco chiara o
con argomentazioni non
Non sempre appropriato l’uso della esaurienti.
terminologia specifica.
Conoscenze essenziali,
eventualmente con qualche
imprecisione.
Procedure risolutive non avviate.
1-2
3-4
Errori in operazioni elementari.
Difficoltà ad applicare procedure note
nella risoluzione di problemi.
5
Qualche imprecisione in quesiti
Esposizione essenziale, con elementari.
argomentazioni poco
Risoluzione corretta di problemi
sviluppate.
utilizzando procedure note.
6
Conoscenze discrete ed uso
abbastanza appropriato della
terminologia specifica.
Esposizione quasi completa, Assenza di errori in quesiti elementari.
con argomentazioni coerenti Risoluzione corretta di problemi che
ma non esaurienti.
richiedono l’utilizzo di procedure note.
7
Conoscenze buone ed uso
appropriato della terminologia
specifica.
Qualche imprecisione in quesiti
Esposizione quasi completa, complessi.
con argomentazioni coerenti
Risoluzione parziale di problemi che
anche se non del tutto
richiedono l’utilizzo di procedure
esaurienti.
complesse o non note.
8
Conoscenze complete e
approfondite. Padronanza nell’uso
della terminologia specifica.
Assenza di errori e imperfezioni in
quesiti complessi.
Esposizione completa, con
argomentazioni coerenti e/o Risoluzione corretta di problemi
significativi apporti personali. utilizzando procedure anche non note
e/o impostate in modo originale.
Non sempre corretto l’utilizzo della
terminologia specifica.
9 - 10
Costituiscono parte integrante della griglia di valutazione le seguenti delibere del Collegio Docenti del 10/02/2015
1. L'alunno rifiuta di farsi interrogare
Premesso che l'alunno è automaticamente giustificato se il giorno prima ha partecipato ad attività integrative particolarmente
significative (Olimpiadi varie discipline, certificazione linguistica...); in tutti gli altri casi si specifica quanto segue:
- l'alunno può giustificarsi 1 volta nel trimestre e 1 nel pentamestre. La volontà di giustificarsi va espressa all'inizio della lezione.
Non si ammette alcuna giustificazione nel caso di prove di recupero e nel caso di interrogazioni programmate.
- Non è altresì possibile giustificarsi le ultime 2 settimane sia nel trimestre che nel pentamestre.
- La giustificazione verrà segnata con la "g", presente nel menù a tendina dei voti del registro elettronico.
- Dopo la giustificazione, se l'alunno persiste nel rifiuto di farsi interrogare, il docente procederà comunque all'interrogazione ed
attribuirà una valutazione.
2. L'alunno non rispetta il termine di consegna di un elaborato da svolgere a casa
Il docente accetterà una mancata consegna a periodo valutativo - trimestre e pentamestre - e fisserà un nuovo termine di
consegna ultimativo, se entro tale termine lo studente non consegna l'elaborato, il docente attribuirà il voto "2"