corrente elettrica

CORRENTE ELETTRICA
Si definisce CORRENTE ELETTRICA un moto ordinato
di cariche elettriche.
Il moto ordinato è distinto dal moto termico, che è
invece disordinato, ed è sovrapposto a questo.
Il moto ordinato (moto di deriva) è imposto dalla
presenza di un campo elettrico all’interno di un
conduttore.
La velocità del moto di deriva è sensibilmente
inferiore a quella del moto termico, però ha verso
costante, mentre il moto termico varia
continuamente.
CORRENTE ELETTRICA
La grandezza fisica che descrive la corrente elettrica
è l’intensità di corrente.
INTENSITA’ DI CORRENTE: quantità di elettricità che
attraversa una qualunque sezione di un conduttore
in un secondo
i
Q
t
Unità di misura: ampère (A)
CORRENTE ELETTRICA
Pur essendo uno scalare l’intensità di corrente è una
grandezza dotata di verso
Per convenzione il verso della corrente elettrica va
dal polo positivo a quello negativo
i
+
-
CORRENTE ELETTRICA
Se l’intensità di corrente è indipendente dal tempo
allora si parla di corrente continua.
Quando l’intensità di corrente varia nel tempo si
parla di corrente variabile.
Un caso particolare di corrente variabile è quella
alternata, in cui l’intensità di corrente varia con
legge sinusoidale.
La corrente domestica è alternata, con una
frequenza di 50 Hz.
Quella fornita da una pila è, al contrario, continua
CORRENTE ELETTRICA
Le condizioni di un conduttore in cui passa corrente
sono opposte a quelle di equilibrio elettrostatico:
• le cariche elettriche sono in movimento
• il campo elettrico non è nullo: infatti è proprio la
sua azione che mantiene in moto le cariche
• il potenziale non è costante
Perché ciò avvenga è necessario evitare che si
stabilisca l’equilibrio nel conduttore
GENERATORE
Si dice generatore un apparecchio in grado di
mantenere ai capi di un conduttore una differenza di
potenziale non nulla
Le condizioni per il passaggio di corrente elettrica
sono dunque:
• una catena ininterrotta di conduttori
• la presenza in essa di almeno un generatore
GENERATORE DI TENSIONE
Si dice generatore di tensione un apparecchio che
mantiene ai suoi poli, o morsetti, una differenza di
potenziale sempre uguale (costante, o comunque ad
andamento fisso, ad esempio sinusoidale) qualsiasi
sia la corrente circolante.
Nella realtà tutti i generatori hanno una caduta di
potenziale all’aumentare dell’intensità di corrente,
quindi un generatore di tensione è in realtà un
dispositivo ideale
GENERATORE DI CORRENTE
Si dice generatore di corrente un apparecchio che
mantiene un’intensità di corrente sempre uguale
(costante, o comunque ad andamento fisso, ad
esempio sinusoidale).
Anche il generatore di corrente è in realtà un
dispositivo ideale
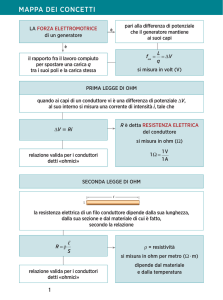
FORZA ELETTROMOTRICE
Si dice FORZA ELETTROMOTRICE di un generatore
la differenza di potenziale che si misura ai suoi capi
a circuito aperto, cioè quando non sta erogando
corrente
• nel generatore di tensione la differenza di
potenziale erogata è uguale alla f.e.m.
• nei generatori reali la d.d.p. erogata è inferiore
alla f.e.m.
• nei generatori di corrente la f.e.m. è infinita
RESISTENZA
Si dice RESISTENZA di un corpo il rapporto tra la
differenza di potenziale ai suoi capi e l’intensità di
corrente che in esso circola
R
V
i
L’unità di misura della resistenza è l’ohm (simbolo Ω)
1
1volt
1am père
RESISTENZA
George Simon Ohm,
1789-1854
PRIMA LEGGE DI OHM
Ohm dedusse una legge sperimentale, che porta
oggi il nome di PRIMA LEGGE DI OHM.
In una larga classe di conduttori, tra cui i metalli e i
liquidi (ma non i gas) la differenza di potenziale e
l’intensità di corrente sono direttamente
proporzionali, ovvero la resistenza è costante
PRIMA LEGGE DI OHM
La prima legge viene di solito espressa nella forma:
V
R i
Che non è altro che la definizione di R scritta in
un’altra forma. Il vero contenuto della prima legge
è che R è costante, ovvero che questa formula è
una vera legge di proporzionalità
CONDUTTORI OHMICI
I conduttori per cui vale la prima legge di Ohm
sono detti ohmici.
I gas, e molti componenti elettronici, come diodi e
transistor, non sono ohmici
RESISORE
Si dice resistore un
elemento elettrico
dotato di una
specifica resistenza.
Nei circuiti elettrici i
resistori sono
etichettati con un
codice a fasce
colorate che ne
indica la resistenza
RESISORE
Il resistore
ideale ha come
unica
caratteristica la
sua resistenza
invariabile.
Questa è,
ovviamente, solo
un’astrazione
SECONDA LEGGE DI OHM
La resistenza di un resistore di sezione costante
(come un filo) è direttamente proporzionale alla
lunghezza ed inversamente proporzionale alla
sezione
R
L
S
RESISTIVITA’
La costante ρ prende il nome di resistività o
resistenza specifica e si misura in ohm∙metro
La resistività dipende dal materiale:
• i metalli hanno bassissima resistività
• al contrario, gli isolanti hanno elevatissima
resistività
• i semiconduttori hanno valori intermedi
RESISTIVITA’
RESISTIVITA’
La resistività dipende anche dalla temperatura:
• nei metalli la resistività aumenta all’aumentare
della temperatura, e si annulla allo zero assoluto
• nei semiconduttori al contrario la resistività
diminuisce all’aumentare della temperatura, e
diventa infinita allo zero assoluto
SUPERCONDUTTIVITA’
In alcuni materiali la resistività si annulla prima di
raggiungere lo zero assoluto: questo stato viene
detto superconduttore.
Il mercurio diventa superconduttore a 4,2K.
Negli anni ’90 sono stati scoperti composti che
diventano superconduttori a temperature fino a
138K, ma il costo di queste sostanze è ancora
eccessivo per un uso pratico su vasta scala
CIRCUITO
Un circuito è una catena di
resistori, generatori e altre
componenti che ha lo scopo di
trasferire energia elettrica da
un punto all’altro del circuito
stesso
CIRCUITO
Elementi di un circuito:
• generatore
• resistore: è caratterizzato dalla sola resistenza
• capacitore: è un condensatore ideale, caratterizzato
dalla sola capacità elettrostatica
• interruttore
• utilizzatore (ad esempio una lampadina)
• induttore
• trasformatore
• diodo
• transistor…
CIRCUITO
Questi elementi
sono indicati con
dei simboli
NODO
Si dice NODO un punto
di un circuito in cui sono
collegati tre o più
componenti del circuito
stesso.
Nel circuito qui
rappresentato ci sono
due nodi, cerchiati in
rosso
RAMO
Si dice RAMO una
catena di conduttori
compresa tra due
nodi.
Nel circuito in figura ci
sono tre rami:
• quello che
comprende E1 ed R3
• quello che
comprende E2 ed R2
• quello che
comprende R1
MAGLIA
Si dice MAGLIA una
catena ininterrotta di
elementi del circuito.
Nel circuito in figura ci
sono tre maglie:
• R1, R3, E1
• R1, R2, E2
• E1, E2, R2, R3
Di queste, però, solo
due sono indipendenti,
perché l’altra è
ottenibile dalla
sovrapposizione delle
prime due
VERSO DELLA CORRENTE
Possiamo attribuire ad
ogni ramo una corrente
orientata secondo un
verso arbitrario.
Le correnti risulteranno
positive se il loro verso
corrisponde a quello
scelto, negative se il
verso è opposto
LEGGI DI KIRCHHOFF
Gustav Robert Kirchhoff
(1824-1887)
LEGGI DI KIRCHHOFF
PRIMA LEGGE
La somma delle intensità delle correnti entranti in
un nodo è uguale alla somma delle intensità
correnti uscenti
E’ una conseguenza della conservazione della
carica elettrica: infatti la quantità di elettricità che
entra in un secondo in un nodo deve essere pari a
quella che esce, altrimenti ci sarebbe creazione o
distruzione di carica
LEGGI DI KIRCHHOFF
SECONDA LEGGE
La somma algebrica delle differenze di potenziale
dei generatori inseriti in ogni maglia è uguale alla
somma delle cadute di potenziale in ogni
elemento della maglia
E’ una conseguenza del teorema della
circuitazione e generalizza la prima legge di Ohm
LEGGI DI KIRCHHOFF
Cadute di potenziale:
• per un resistore:
• per un capacitore:
• per un induttore:
R i
Q
C
di
L
dt
RESISTORI IN SERIE
Due resistori in serie
equivalgono a un unico
resistore la cui
resistenza è la somma
delle resistenze
V
iR1 iR2
V
i( R1 R2 )
Per la seconda legge di Kirchhoff
Raccogliendo i
E poi, ponendo:
Si ha la tesi
R1 R2
V
iR
R
GENERATORE REALE
Un generatore reale può essere pensato
come un generatore ideale con forza
elettromotrice f in serie con un resistore di
resistenza r. Se ΔV è la ddp vista
effettivamente ai capi del generatore, per la
seconda legge di Kirchhoff:
f
V
ir
f
ir
E quindi:
V
Ovvero, la tensione effettivamente erogata è
minore di f, e la diminuzione è proporzionale
a i (r si dice resistenza interna)
RESISTORI PARALLELO
Due resistori in
parallelo equivalgono a
un unico resistore la cui
resistenza è il reciproco
della somma dei
reciproci delle
resistenze
Applicando la seconda legge di Kirchhoff alla maglia R1
Applicando la seconda legge di Kirchhoff alla maglia R2
Applicando la prima legge di Kirchhoff a uno dei nodi
i
V
i1R1
V
i2 R2
i1 i2
RESISTORI PARALLELO
Ricavando i1 e i2 dalle prime due equazioni e sostituendo nella terza
i
V
R1
Ponendo poi:
Si ha la tesi:
V
R2
Raccogliendo
1
R
V
1
R1
iR
i
1
R2
1
R1
1
R2
V
SCARICA DEL
CONDENSATORE
Consideriamo un
condensatore carico con
carica Qo posto in serie a un
resistore. Quando
l’interruttore viene chiuso il
condensatore si scarica.
Poiché nella maglia non vi
sono generatori, per la
seconda legge di Kirchhoff:
iR
Q
C
0
SCARICA DEL
CONDENSATORE
Poiché i è la derivata di Q rispetto a t possiamo
anche scrivere:
dQ
Q
R
dt
C
0
dQ
dt
Q
CR
dQ
Q
1
dt
CR
SCARICA DEL
CONDENSATORE
Integrando membro a membro:
dQ
Q
ln Q
Q Qo e
1
dt
CR
1
t ln Qo
CR
1
t
CR
SCARICA DEL
CONDENSATORE
Ovvero, il processo di scarica di un condensatore nel
tempo segue un andamento esponenziale
Q Qo e
1
t
CR
CR indica il tempo di scarica: quindi un
condensatore si scaricherà tanto più lentamente
quanto maggiori sono capacità e resistenza
LAVORO ELETTRICO
Un generatore inserito in un circuito compie un
lavoro che viene trasferito alle altre componenti
del circuito.
Poiché la differenza di potenziale è lavoro diviso
carica il lavoro elettrico sarà:
L Q
V
Dove ΔV è la differenza di potenziale del
generatore e Q è la carica spostata.
POTENZA ELETTRICA
Poiché l’intensità di corrente è carica diviso
tempo allora Q è intensità per tempo, quindi:
L
V i t
Dividendo per il tempo si ottiene la formula per
la potenza elettrica
W
V i
EFFETTO JOULE
Il lavoro elettrico
compiuto in un resistore
viene convertito in calore.
Questo fenomeno viene
detto “effetto Joule”.
In tutti i dispositivi di
riscaldamento elettrico
viene sfruttato l’effetto
Joule, che è invece
indesiderato nella
trasmissione di corrente
lungo le linee elettriche
EFFETTO JOULE
Per la prima legge di Ohm
V
iR
Quindi, la potenza calorica sviluppata per effetto
Joule si può scrivere in due modi
W
Ri
2
W
V
R
2
EFFETTO TERMOELETTRICO
Zn
+
+
+
+
-
Cu
Se si uniscono due
metalli con diversi,
come ad esempio
rame e zinco, una
piccola quantità di
elettroni si trasferisce
in quello più
elettronegativo,
creando quindi una
differenza di
potenziale alla
giunzione
EFFETTO TERMOELETTRICO
Zn
+
+
+
+
-
Cu
Questo passaggio è
favorito dall’energia
termica che aiuta gli
elettroni a compiere il
balzo, quindi la ddp
che si genera
aumenta
all’aumentare della
temperatura
EFFETTO TERMOELETTRICO
Se si tengono due
giunzioni a
temperatura diversa la
ddp di potenziale in
una non annulla
esattamente l’altra,
quindi nel circuito può
passare una debole
corrente
EFFETTO TERMOELETTRICO
Questo effetto non è
pratico per produrre
corrente, ma è molto
utile per misurare
differenze di
temperatura
(termocoppia)