Circuito con resistori in serie.

** ITN - Caboto - Gaeta ** Fisica - prof. Vindice Luigi **IISS-Caboto- Gaeta**Fisica-prof. Vindice Luigi-

Il resistore. (studiare da p.230)
La 1° legge di Ohm dice che:
R
V
i
Ovvero
V  R  i
Dove:
R= resistenza elettrica []
V= differenza di potenziale [V]
I= intensità di corrente elettrica [A]
****

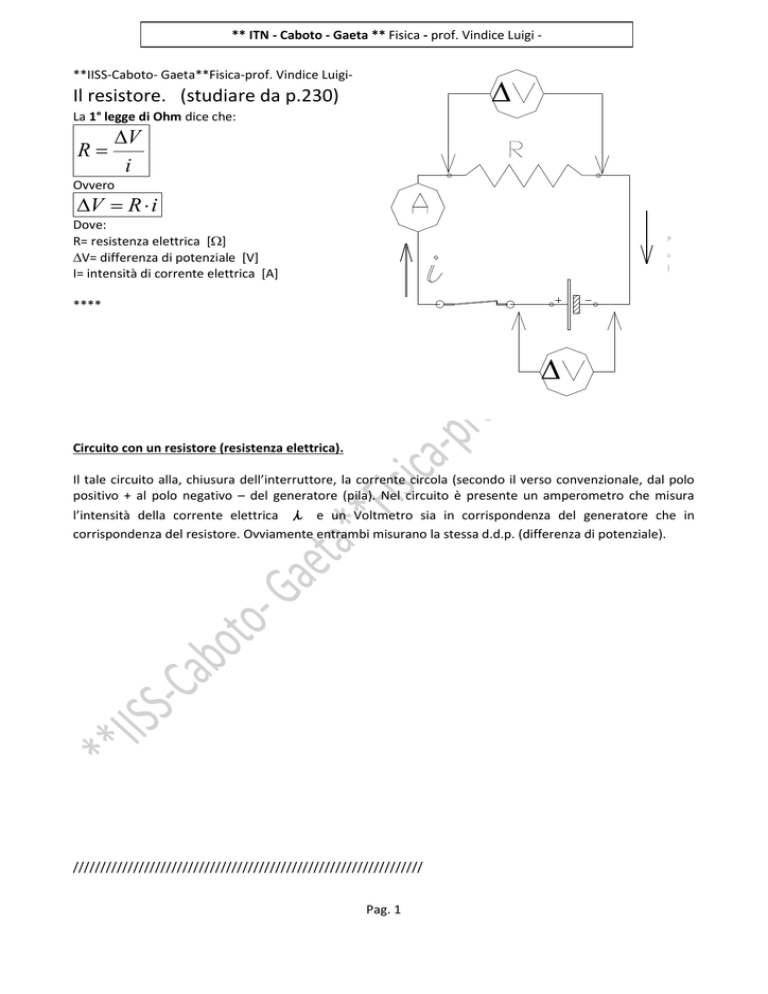
Circuito con un resistore (resistenza elettrica).
Il tale circuito alla, chiusura dell’interruttore, la corrente circola (secondo il verso convenzionale, dal polo
positivo + al polo negativo – del generatore (pila). Nel circuito è presente un amperometro che misura
l’intensità della corrente elettrica i e un Voltmetro sia in corrispondenza del generatore che in
corrispondenza del resistore. Ovviamente entrambi misurano la stessa d.d.p. (differenza di potenziale).
////////////////////////////////////////////////////////////////
Pag. 1
**IISS-Caboto- Gaeta**Fisica-prof. Vindice Luigi-
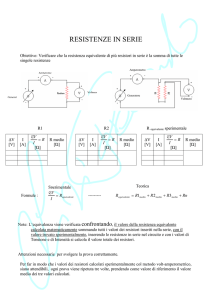
Circuito con resistori in serie.
Vogliamo trovare il valore del resistore equivalente (con il quale si
ottengono gli stessi risultati del circuito di resistori) per questo
tipo di circuito.
In tal caso per semplicità consideriamo due resistori.
E’ evidente che il flusso di corrente che attraversa R1 e R2 è lo
stesso.
Per la legge della conservazione dell’energia la somma V1+V2
deve necessariamente essere V del generatore.
All'uopo citiamo la "legge della maglia" o seconda legge di
Kirchhoff il cui enunciato è: la somma algebrica delle differenze di
potenziale rilevate su un circuito chiuso in un giro completo è
nulla.
Relativamente a V vogliamo far notare che essa rappresenta
l’energia necessaria alle particelle elettriche per spostarsi lungo il
filo. Quindi senza il V non è possibile che possa avvenire il moto
delle cariche elettriche.
V  R  i
V  V1  V2  R1  i  R2  i
V  R1  i  R2  i
V  i  R1  R2 
V
 R1  R2
i
Come si vede DV e
totale.
Pertanto:
i
sono valori totali che forniscono la R
R  R1  R2
Quindi in generale:
n
R   Ri R1  R2  ....  Rn
i 0
////////////////////////////////////////////////////////////////////////////////////
Pag. 2



**IISS-Caboto- Gaeta**Fisica-prof. Vindice Luigi-
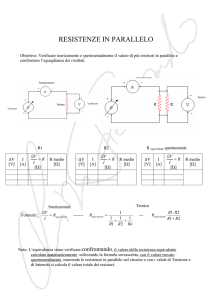
Circuito con resistori in parallelo.
Vogliamo trovare il valore del resistore equivalente (con il quale si
ottengono gli stessi risultati del circuito di resistori) per questo
tipo di circuito.
In tal caso per semplicità consideriamo due resistori.
E’ evidente che il flusso di corrente che attraversa R1 e R2
inizialmente (prima del nodo A) è
i
e poi si suddivide in i1
Per la conservazione della quantità di carica la somma

i2 .
i1+i2
ovviamente deve essere i . Inoltre teniamo presente che il 1°
legge di Kirchhoff o teoria del nodo dice che: in ogni nodo la
somma (algebrica) delle correnti deve essere nulla.
Quindi la "legge dei nodi" o prima legge di Kirchhoff dice che: la
somma delle correnti che entrano in un nodo deve essere uguale
alla somma delle correnti che escono dal nodo stesso.
Il V in corrispondenza di A e B deve essere la V del generatore.
i
V
R
1
V V
1 

 V    
R1
R2
 R1 R2 
i
1
1
 
V R1 R2
1 1
1
 
R R1 R2
1
R
1
1

R1 R2
i  i1  i2 
Quindi in generale:
n
1
1 1 1
1
  
 ... 
R i 1 Ri R1 R2
Rn
Ovvero:
R
1
n
1

i 1 Ri

1
1 1
1

 ... 
R1 R2
Rn
////////////////////////////////////////////////////////////////////////////////
Pag. 3
