CAMPO ROTANTE DI GALILEO FERRARIS.
È noto che un solenoide percorso da corrente
elettrica dà origine nel suo interno a un campo
magnetico H che ha come direzione quella del suo
asse come mostrato in fig.1. Se esso e generato da
una corrente alternata sinusoidale anch'esso è
sinusoidale e lo possiamo esprimere con la
seguente relazione:
N
H
I
l
Fig.1
N
N
× i (t ) = × I M sen(ω ⋅ t )
l
l
Il campo prodotto dalla (1) può essere rappresentato istante per istante mediante due
HM
vettori di ampiezza costante S = D =
e ruotanti in senso opposto con velocità
2
angolare costante e uguale a n.
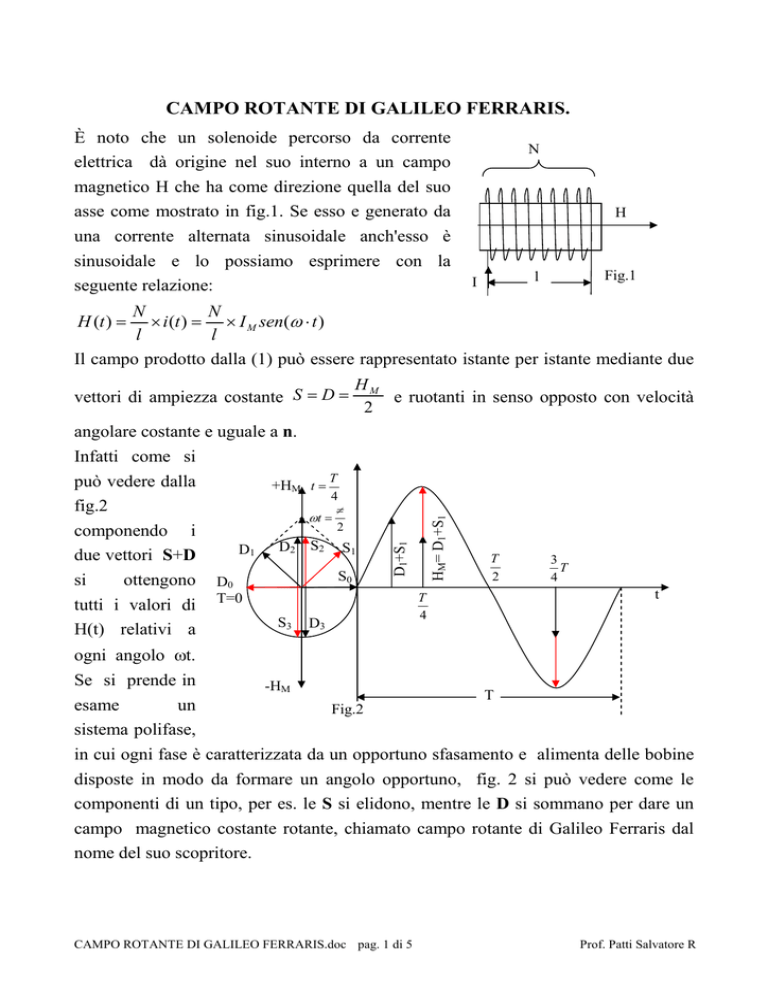
Infatti come si
T
può vedere dalla
+HM t =
4
fig.2
π
ωt =
2
componendo i
D2 S2 S1
D1
due vettori S+D
T
3
T
2
S0
4
si
ottengono D0
t
T
tutti i valori di T=0
4
S3 D3
H(t) relativi a
HM= D1+S1
D1+S1
H (t ) =
ogni angolo ωt.
Se si prende in
-HM
T
esame
un
Fig.2
sistema polifase,
in cui ogni fase è caratterizzata da un opportuno sfasamento e alimenta delle bobine
disposte in modo da formare un angolo opportuno, fig. 2 si può vedere come le
componenti di un tipo, per es. le S si elidono, mentre le D si sommano per dare un
campo magnetico costante rotante, chiamato campo rotante di Galileo Ferraris dal
nome del suo scopritore.
CAMPO ROTANTE DI GALILEO FERRARIS.doc pag. 1 di 5
Prof. Patti Salvatore R
CAMPI ROTANTI BIFASI
F1
Un campo rotante bifase si può
realizzare con due avvolgimenti posti a
90° come in fig.3 e alimentati con due
correnti alternate aventi l'una rispetto
all'altra uno sfasamento di un quarto di
periodo.
Esse danno un campo magnetico
H1 (t ) = H M sen(ω ⋅ t )
I1
X1
I2
P2
e
H 2 (t ) = H M sen(ω ⋅ t + 90)
Si ha che per t=0, H1=0 e H2=HM
come mostrato rispettivamente in fig.4a e 4b.
F2
P1
X2
Fig. 3
Se
adesso
si
sovrappongono i due
D2
D1, D2
D1
S1
campi si ottiene come
S2
S
1
S2
mostrato fig.4(a+b) ed
evidenziato in fig. 4c e
fig .4(a+b)
fig. 4a
fig. 4b
fig. 4d che le
due
componenti D1 e D2 si
D1
S2
S1
sommano e ruotano con
velocità costante e
D2
uguale per ambedue,
fig. 4c
fig . 4d
mentre S1 e S2 ruotano
Fig. 4
sempre mantenendosi
opposti ed eliminandosi. Pertanto abbiamo ottenuto un campo magnetico costante di
intensità pari a D1 + D2 =
HM HM
+
= H M = COSTANTE che ruota con velocità ω, dove ω
2
2
è la pulsazione della corrente che lo genera fig.4
CAMPI ROTANTI TRIFASI.
Analogo risultato può ottenersi con sistemi trifasi o polifasi. Per quanto riguarda i
sistemi trifasi si ha che gli avvolgimenti devono essere posti a 120° elettrici con le
correnti sfasate fra loro di 120°. Le tre correnti devono avere uguale valore efficace.
CAMPO ROTANTE DI GALILEO FERRARIS.doc pag. 2 di 5
Prof. Patti Salvatore R
Esse daranno luogo quindi a tre campi magnetici
H1 (t ) = H M sen(ω ⋅ t ) ,
H 2 (t ) = H M sen(ω ⋅ t + 120) e H 3 (t ) = H M sen(ω ⋅ t − 120)
Infatti se i tre avvolgimenti identici non fossero anch’essi sfasati di 120 gradi avremo
la seguente condizione, ma disposti
I1
F1
sullo stesso asse alimentandoli con un
sistema trifase diamo origine a tre
D1
campi magnetici le cui componenti
Destre D e Sinistre S sono illustrate
rispettivamente nelle figure 5a, 5b, 5c
x1
seguenti:
Per t=0
S1
H1 (t ) = H M sen(ω ⋅ t ) = 0
Fig. 5a
P1
I2
F2
H 2 (t ) = H M sen(ω ⋅ t + 120)
120°
S2
X2
120°
P2
H 3 (t ) = H M sen(ω ⋅ t − 120)
Possiamo comporre questi campi
magnetici e otteniamo due terne una
sinistrorsa e una destrorsa la cui
somma dà come valore zero come è
evidente nella figura 6
D1
S3
I3
D2
Fig. 5b
F3
240°
S3
X3
D3
,
240°
Fig. 5c
S2
P3
D3
D2
S1
Fig. 6
CAMPO ROTANTE DI GALILEO FERRARIS.doc pag. 3 di 5
Prof. Patti Salvatore R
I1
A
questo
punto
ruotiamo
gli
avvolgimenti ognuno di 120 gradi
rispetto all’altro.
F1
D1
x1
Per far ciò lasciamo fermo il primo
avvolgimento, fig.7a .
S1
Fig. 7a
P1
X2
i2
F2
D2
Ruotiamo
il
secondo di 120°
in
senso
antiorario come
in figura 7b
S2
S2
X2
i2
D2
F2
Fig. 7b
P2
I3
F3
P3
D3
Il
terzo
avvolgimento deve
essere ruotato di
240 gradi fig. 7c
S3
S3
X3
F3
D3
,
i3
P3
X3
Fig. 7c
Se componiamo il tutto e sommiamo vettorialmente le componenti sia le componenti
destrorse che sinistrorse, fig. 8, otteniamo che il valore massimo del campo
CAMPO ROTANTE DI GALILEO FERRARIS.doc pag. 4 di 5
Prof. Patti Salvatore R
magnetico rotante generato è pari a 3 volte la componente destrorsa D, quindi è i 3/2
del valore massimo di ciascuno dei tre campi alternati. Esso ruota con velocità
angolare ω e compie un giro in un periodo.
Mentre le componenti sinistrorse formano, fig.8, una terna di vettori rotanti S1,S2,S3,
equilibrata e pertanto e sempre nullo il loro effetto.
Il vettore rotante risulta quindi H D = 3 ⋅ D =
3
H M = COSTANTE
2
X2
X2
i1
F1
P3
D1, D2, D3
P2
S2
S3
X1
X1
i2
F3
F2
S1
i3
P1
X3
X3
fig.8
Se scambiamo una fase avviene che le componenti sinistrorse si sommano e danno il
campo magnetico rotante costante
e pari ai H S = 3 ⋅ S =
3
H M , mentre le tre
2
componenti destrorse si annullano. Si desume da ciò che per invertire la marcia è
sufficiente uno scambio di fase.
SISTEMI POLIFASI
Per sistemi polifasi si può ottenere analogo risultato considerando n avvolgimenti
identici, con gli assi incidenti in un punto o e spostati di un angolo costante uguale a
360/n, alimentati con n correnti sfasate l'una rispetto all'altra di T/n. Il campo
ottenuto avrà un valore di n ⋅
HM
dove HM è il valore massimo del campo generato in
2
ogni avvolgimento.
CAMPO ROTANTE DI GALILEO FERRARIS.doc pag. 5 di 5
Prof. Patti Salvatore R












