4
4.0.1
FUNZIONE ESPONENZIALE E FUNZIONE LOGARITMO
Esponenziale.
Nella prima sezione abbiamo definito le potenze con esponente reale. Vediamo ora in dettaglio le proprietà
della funzione esponenziale x 7−→ ax , a > 0, x ∈ R.
Proprietà 4.1 (Proprietà dell’esponenziale). Siano x, z ∈ R e a > 0. Allora
(i) a0 = 0.
(ii) ax > 0
∀x ∈ R.
(iii) ax+z = ax az
∀x ∈ R.
(iv) Se a > 1, allora: ax < az ⇐⇒ x < z.
(vi) Se 0 < a < 1, allora: ax > az ⇐⇒ x < z.
(v) Se a > 1, allora:
lim
x→=−∞
(vii) Se 0 < a < 1, allora:
ax = 0 e
lim
x→=−∞
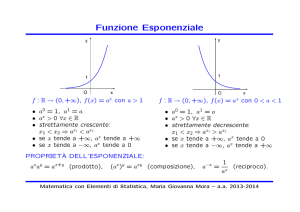
Esempio 4.2 Grafico di f (x) = 2x e g(x) =
lim
x→=+∞
ax = +∞ e
1 x
2
ax = +∞.
lim
x→=+∞
ax = 0.
= 2−x = f (−x).
y
f (x) = 2x
g(x) = 2−x
1
b
x
La funzione f (x) = ax , con a > 1, gode delle seguenti proprietà.
• f ha come dominio tutta la retta reale.
• Intersezioni con gli assi: punto di coordinate (0,1).
• f (x) > 0 ∀x ∈ R.
• f è strettamente crescente su R.
•
lim
x→=−∞
ax = 0 e
lim
x→=+∞
ax = +∞.
38
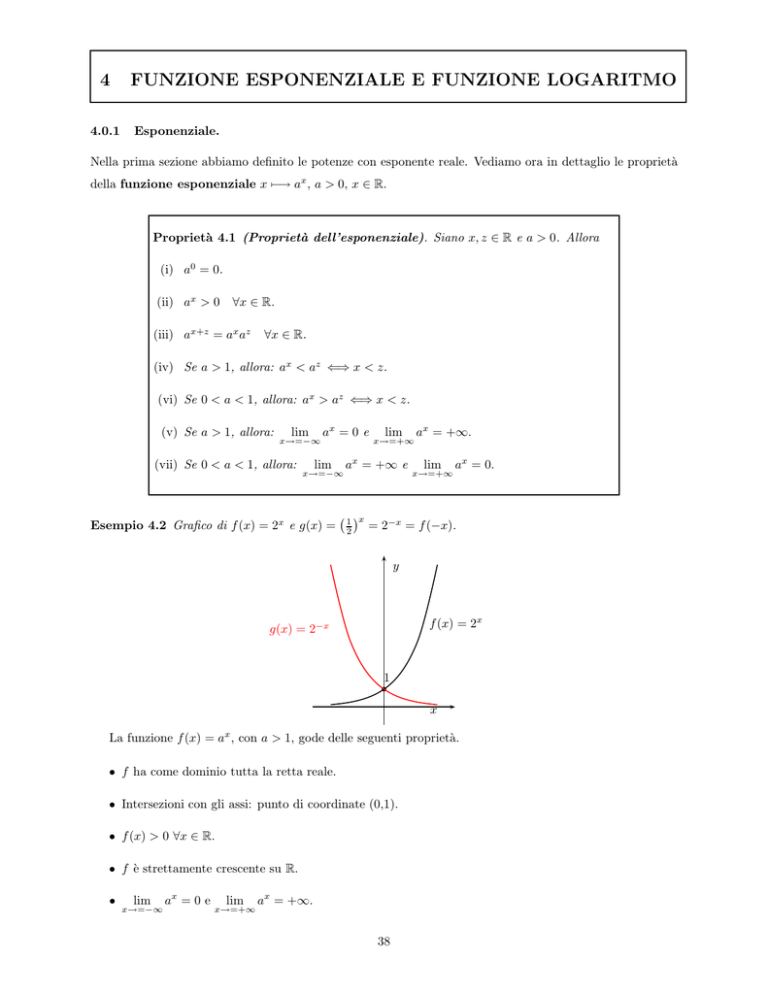
La funzione f (x) = ax , con 0 < a < 1, gode delle seguenti proprietà.
• f ha come dominio tutta la retta reale.
• Intersezioni con gli assi: punto di coordinate (0,1).
• f (x) > 0 ∀x ∈ R.
• f è strettamente decrescente su R.
•
lim
x→=+∞
ax = 0 e
lim
x→=−∞
ax = +∞.
Proprietà 4.3 (Altre proprietà delle potenze). Siano a, b > 0, x, y ∈ R.
Allora
(i) (a · b)x = ax · bx .
y
(ii) (ax ) = axy .
(iii) ax+y = ax ay
∀x ∈ R.
(iv) ax < bx ⇐⇒ a < b ∀x > 0
(v) ax > bx ⇐⇒ a < b ∀x < 0
Esempio 4.4 Il disegno sottostante illustra le proprietà (iv) e (v) con a = 2 e b = 3.
y
f (x) = 2x
g(x) = 3x
1
b
x
Esercizio 4.5 Risolvere la disequazione:
3−x > 1.
Ricordiamo che 1 = 30 , quindi
3−x > 1 ⇐⇒ 3−x > 30 ⇐⇒ −x > 0 ⇐⇒ x < 0
39
4.1
Numero “e” di Nepero
Definizione 4.6 Definiamo il “numero e” di Nepero mediante
n
1
.
e = lim
1+
n→+∞
n
• Osserviamo che il limite nella definizione presenta la forma di indecisione 1∞ . Inoltre l’esistenza del
n
limite è garantita dal fatto (non ovvio) che la successione n 7−→ 1 + n1 è monotona crescente e limi-
tata, quindi il limite esiste ed è finito (si veda per esempio Bramanti, Pagani, Salsa, ”MATEMATICA
Calcolo infinitesimale e algebra lineare”, Zanichelli).
• il numero “e” di Nepero è irrazionale, ovvero ha infinite cifre dopo la virgola. Una prima approssimazione di “e” è la seguente:
e = 2, 718....
• Ricordiamo la definizione di k! con k intero non negativo. Abbiamo
0! = 1 k! = k · (k − 1) · (k − 2) · (k − 3) · · · 3 · 2 · 1
Si dimostra che
ex =
+∞ k
X
x
k=0
k!
∀x ∈ R.
In particolare
e=
+∞
X
1 1
1
1
=1+1+ + +
+ ···
k!
2 6 24
k=0
Questa espressione permette di calcolare valori approssimati di “e”.
Esempio 4.7 Grafico di f (x) = ex e g(x) = e−x .
y
g(x) = e−x
f (x) = ex
1
b
x
40
4.2
Logaritmo.
La funzione logaritmo è definita come la funzione inversa della funzione esponenziale. Più precisamente se
a > 0 e a 6= 1, allora il logaritmo in base a di x > 0 è il numero reale y dato da:
y = loga x ⇐⇒ ay = x.
In altre parole y = loga x è l’esponente da dare alla base a per ottenere l’argomento x del logaritmo.
Per esempio log2 8 = 3, infatti 23 = 8. In generale dalla definizione segue loga ay = y.
Proprietà 4.8 (Proprietà del logaritmo). Siano x, z > 0, a > 0 e a 6= 1. Allora
(i) aloga x = x;
(ii) loga 1 = 0;
(iii) loga a = 1;
(iv) loga (xz) = loga x + loga z;
(v) loga (xβ ) = β loga x;
(vi) loga
x
z
= loga x − loga z;
(vii) loga x = − log a1 x;
(viii) loga x =
logb x
logb a ,
∀b > 0 e b 6= 1.
Dimostrazione.
(i) L’uguaglianza aloga x = x segue direttamente dalla definizione;
(ii) loga 1 = y ⇐⇒ ay = 1 ⇐⇒ y = 0.
(iii) loga a = y ⇐⇒ ay = a ⇐⇒ y = 1.
(iv) Dalla (i) otteniamo: loga (xz) = loga x + loga z ⇐⇒ xz = aloga (xz) = aloga x+loga z = aloga x aloga z = xz.
(v) Dalla (i) otteniamo:
loga (xβ ) = β loga x ⇐⇒ aloga (x
β
)
= aβ loga x ⇐⇒ aloga (x
(vi) Dalla (iv) e dalla (v) otteniamo: loga
x
z
β
)
= aloga x
β
β
⇐⇒ (xβ ) = (x) ;
= loga x z −1 = loga x + loga z −1 = loga x − loga z;
(vii) Dalla (i) otteniamo: loga x = − log a1 x ⇐⇒ aloga x = a
− log 1 x
a
= a−1
log 1
a
x
=
1x
1 log a
a
= x;
(viii) Dalla (i) otteniamo:
loga x =
logb x
logb a
⇐⇒ logb x = logb a loga x ⇐⇒ blogb x = blogb a loga x = blogb a
41
loga x
= aloga x .
⊔
⊓
Esempio 4.9 Grafico di f (x) = loga x e g(x) = log a1 x = −f (x). Nel disegno abbiamo preso a = 2. Come
osservato nella sottosezione ??, il grafico di f (x) = loga x è simmetrico al grafico di f −1 (x) = ax rispetto
alla bisettrice di equazione y = x.
y
f (x) = loga x
1b
x
g(x) = log a1 x
Definizione 4.10 La funzione f (x) = ln x = loge x prende il nome di logaritmo naturale.
La funzione f (x) = loga x, con a > 1 (quindi in particolare f (x) = ln x), gode delle seguenti proprietà.
• Il dominio di f è la semiretta positiva (0, +∞).
• Intersezioni con gli assi: punto di coordinate (1,0).
• f (x) > 0 per x > 0 e f (x) < 0 per 0 < x < 1.
• f è strettamente crescente su R, ovvero: loga x < loga z ⇐⇒ x < z.
• lim loga x = −∞ e lim loga x = +∞.
x→0+
x→+∞
• La retta di equazione x = 0 è un asintoto verticale.
La funzione f (x) = logb x, con 0 < b < 1, gode delle seguenti proprietà.
• Il dominio di f è la semiretta positiva (0, +∞).
• Intersezioni con gli assi: punto di coordinate (1,0).
42
• f (x) > 0 per 0 < x < 1 e f (x) < 0 per x > 0.
• f è strettamente decrescente su R, ovvero: loga x < loga z ⇐⇒ x > z.
• lim loga x = +∞ e lim loga x = −∞.
x→+∞
x→0+
• La retta di equazione x = 0 è un asintoto verticale.
Esempio 4.11 Risolvere la disequazione
ln(x) > 3.
Essendo 3 = ln(e3 ) ed essendo f (x) = ln(x) una funzione strettamente crescente, otteniamo:
ln(x) > 3 ⇐⇒ ln(x) > ln(e3 ) ⇐⇒ ln(x) > ln(e3 ) ⇐⇒ x > e3 .
Esempio 4.12 Risolvere la disequazione
1
log2 x < − .
3
Essendo
1
3
1
1
= log2 (2− 3 ) = log2 ( √
3 ) ed essendo f (x) = log2 x una funzione strettamente crescente, otteniamo:
2
log2 x <
1
⇐⇒ log2 x < log2
3
1
√
3
2
1
.
⇐⇒ 0 < x < √
3
2
y
y = log2 x
1
√
3
b2 b 1
x
y=
43
− 13