Economia Politica 2 - MICROECONOMIA

Economia Politica 2 - MICROECONOMIA
ESERCITAZIONE 6
Mercoledì 19 Novembre 2003
SOLUZIONI
PRIMA PARTE
Si risponda alle seguenti domande:
(N.B. le risposte riportate rappresentano una traccia per lo studente, a cui è richiesto di argomentare
compiutamente)
1. Si descriva la condizione di ottimo del monopolista, indicando quale livello di output egli
sceglie al fine di massimizzare il profitto e perché.
Un monopolista massimizza il profitto scegliendo il livello di output per il quale il ricavo
marginale uguaglia il costo marginale. Essendo il profitto economico uguale alla distanza
verticale tra ricavo totale e costo totale, tale distanza è massimizzata quando le curve di ricavo
totali e di costo totale hanno la stessa inclinazione (vedi grafico a pag.393 Frank nuova
edizione)
2. L’impresa Hein&Ken è monopolista nel settore della produzione di birra: questa
configurazione è efficiente?
No. Se comparato con la concorrenza perfetta,che porta ad un’allocazione efficiente delle
risorse, il monopolio comporta la produzione di una quantità inferiore ad un prezzo più alto.
1
3. La discriminazione di prezzo del primo ordine fa sì che il monopolista produca di più e ad
un prezzo minore che in assenza di discriminazione? Argomentare la risposta.
In presenza di discriminazione perfetta (o del prim’ordine), il monopolista è in grado di
vendere ogni unità di prodotto al prezzo massimo che il consumatore sarebbe disposto a
pagare: ciò significa che egli produce la massima quantità possibile (quella che sarebbe
prodotta in concorrenza perfetta, quindi maggiore di quella di monopolio) ad un prezzo
corrispondente alla disponibilità a pagare di ciascun consumatore, che leggiamo sulla curva di
domanda (e per le unità aggiuntive è inferiore al prezzo di monopolio).
4. Per quale motivo si parla di “perdita netta di monopolio”?
La regola di massimizzazione del profitto del monopolista comporta il passaggio di parte del
sovrappiù del consumatore al monopolista; tuttavia, il fatto che il monopolista produca una
quantità inferiore rispetto a quella prodotta nella configurazione efficiente (corrispondente alla
concorrenza perfetta) e ad un prezzo più alto fa sì che la restante parte del sovrappiù non vada
a beneficio di alcun membro della società: si parla pertanto di perdita netta.
5. Il monopolista produce in corrispondenza del tratto elastico della curva di domanda. Vero o
falso? Argomentare la risposta.
Vero. L’obiettivo del monopolista consiste nella massimizzazione del profitto: se egli
producesse un livello di output sul tratto inelastico della curva di domanda, significherebbe che
aumentando il prezzo potrebbe conseguire un più elevato ricavo totale (il profitto potrebbe
crescere ulteriormente: non sarebbe pertanto massimizzato!)
6. Per il monopolista il prezzo non è uguale al ricavo marginale. Si dia una motivazione
analitica e se ne spieghi il significato.
Per il monopolista, il ricavo marginale è sempre inferiore al prezzo (ad eccezione del caso
corrispondente al monopolista perfettamente discriminante). Ricordando la definizione di
ricavo marginale, possiamo scrivere:
MR 
 TR  PQ  *Q
P

 PQ   Q
Q
Q
Q
che mette in luce come il ricavo marginale possa essere considerato come la somma algebrica
tra l’aumento del ricavo derivante dalle nuove vendite (P) e la perdita nel ricavo che è dovuta
2
al fatto che la produzione che si sarebbe comunque venduta è offerta ad un prezzo inferiore
 P
 Q*
 . Essendo il secondo addendo negativo, MR < prezzo.
Q 

SECONDA PARTE
ESERCIZIO 1
Un monopolista fronteggia una curva di domanda di mercato: P = 100 – 4q
I suoi costi di breve periodo sono dati dalla funzione: CT = 20q
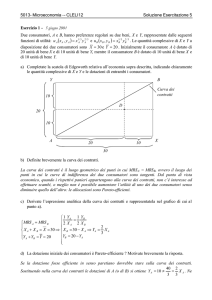
a) Disegnate la funzione di domanda, la curva MR e la curva MC.
P
Profitto di
monopolio
100
60
Perdita secca di

E

monopolio

MC
20
RM
10
AR = domanda
20
q
25
b) Calcolate l’equilibrio del monopolista: quantità (q*) e prezzo (P*).
MC = MR,
dalla funzione di costo: MC = 20 (costante)
dalla funzione di domanda inversa: MR = 100 – 8q, da cui:
100 –8q = 20  80 = 8q  q* = 10, sostituisco nella funzione di domanda :
P = 100 –4q*  P* = 60
c) Calcolate e disegnate l’area del profitto (Π) di monopolio.
Π = R – C  (100q – 4q2) – 20q
Π(q*) = 1000 – 400 – 200 = 400, profitto di monopolio  coincide con il rettangolo
scuro nella figura (Area ).
Può essere alternativamente ricavato come: Π = AVΠ ·q* , profitto medio per la
quantità di equilibrio, dove AVΠ = AR – AC
(60 – 20) ·10  Π = 400.
d) Calcolate e disegnate la perdita secca di monopolio e motivatene l’esistenza.
3
Per calcolare la perdita secca di monopolio devo preventivamente calcolare quale
sarebbe la quantità prodotta in concorrenza perfetta: AR = MC = P
Qui: 100 –4q = 20  80 = 4q  q* = 20, quantità di equilibrio di concorrenza.
La perdita secca di monopolio è pari all’area del triangolo scuro (area ) e discende dal
fatto che a un prezzo superiore al MC, il prezzo di monopolio, l’offerta scende: una
parte di produzione non viene realizzata e non può essere appropriata, in termini di
surplus, né dal consumatore, né dal produttore.
Perdita = (60 – 20) ·(20 – 10) / 2 = 400/2 = 200
e) In che senso (ed eventualmente per chi) la discriminazione al prezzo del I ordine
(discriminazione perfetta) sarebbe preferibile?
La discriminazione perfetta prevede che ad ogni consumatore venga applicato
esattamente il proprio prezzo di riserva (la cifra massima che il consumatore è disposto
a pagare per consumare una unità di bene). In questo modo la produzione cresce oltre la
quantità di equilibrio di monopolio (q* = 10). Il monopolista infatti non è costretto ad
abbassare il prezzo su tutte le unità inframarginali. La produzione cresce fino a q* = 20,
quantità di equilibrio di concorrenza perfetta.
I profitti del monopolista sono ora coincidenti col surplus totale dell’economia e
precisamente a Π = 20*80/2 = 800.
Il benessere complessivo della società cresce, perché viene meno la perdita secca di
monopolio precedentemente presente, il surplus del monopolista cresce (nel caso in
esame raddoppia) perché il suo profitto si accresce della precedente area di perdita secca
e del precedente surplus del consumatore. Quest’ultimo è l’unico a peggiorare la propria
posizione in termini di benessere, dal momento che il suo surplus viene trasferito al
monopolista. Ma in termini di efficienza, questa situazione risulta preferibile rispetto al
monopolista non discriminante.
Riassumendo, in equilibrio di monopolio:
surplus del consumatore = area ; surplus del produttore = area ; perdita secca di
benessere = area ; surplus dell’economia = +.
In presenza di discriminazione perfetta:
surplus del consumatore  si annulla; surplus del produttore = area ++; perdita
secca di benessere  si annulla; surplus dell’economia = ++.
Supponete ora che venga imposta una tassa sul monopolista, di aliquota t proporzionale alla
quantità prodotta, e che l’aliquota sia pari a: t = 8.
f) Calcolate il nuovo equilibrio del monopolista: quantità (q*) e prezzo (P*); calcolate inoltre il
profitto di monopolio (Π) e l’entrata fiscale (T) per l’amministrazione finanziaria.
Π = R – C –tq
Π = 100q – 4q2 – 20q –8q = 72q –4q2, la massimizzazione impone che:
Π’ = 0  72 –8q = 0  q* = 9, produzione di equilibrio del monopolista dopo
l’introduzione della tassazione
P = 100 –4q* = 100 – 36  P* = 64
Π = (100q – 4q2) – 20q - 8q per q* = 9 dà Π = 324 (profitto del monopolista)
L’entrata tributaria complessiva è pari a T = t ·q* = 8 ·9 = 72
Il surplus del consumatore = 9*36/2=162
4
(si può notare come il surplus totale dell’economia si riduca a 324+72+162=558, con
una diminuzione dell’efficienza complessiva di 42 unità rispetto alla situazione anteimposta, che vedeva un surplus totale di 400+200=600).
ESERCIZIO 2
Un monopolista fronteggia la seguente curva di domanda P = a - bQ.
a)
Sapendo che i costi totali di produzione sono del tipo TC = cQ, si calcoli l’equilibrio
(prezzo, quantità e profitti).
b)
Si calcoli analiticamente e si mostri graficamente la perdita secca.
Soluzione:
a)
Il monopolista massimizza i profitti  = P*Q – TC, cioè in questo caso:
max  = (a – bQ)*Q – cQ,
la cui condizione di primo ordine d / dQ = a – bQ – bQ – c = 0.
Riscritta tale condizione equivale all’utilizzo della regola MR=MC, ovvero a-2bQ=c
(MR per funzione di domanda lineare è equivalente ad una retta con stessa intercetta
verticale della funzione di domanda e doppio coefficiente angolare).
Risolvendo per Q la precedente espressione troviamo la quantità di equilibrio per il
monopolista: QM = (a-c) / 2b.
Se sostituiamo la quantità d’equilibrio nella funzione di domanda otteniamo il prezzo di
equilibrio P M = a-b*(a-c) / 2b che, semplificata, fornisce P M =(a+c)/2.
Infine, i profitti del monopolista  = QM* P M – c* QM; sostituendo nell’espressione prezzo e
quantità d’equilibrio, otteniamo: [(a-c) / 2b]*[ (a+c)/2] – c*[(a-c) / 2b]. Dopo semplici
calcoli e semplificazioni, arriviamo a  = (a-c)2 / 4b.
b)
Dapprima illustriamo graficamente la situazione di monopolio con i valori trovati ed
evidenziamo sul grafico l’area corrispondente alla perdita secca:
5
P
EM
PM
MR
D
c
ECP
A
QM
QCP
Q
Q
l triangolo EMAECP rappresenta graficamente la perdita secca.
Per calcolarne analiticamente l’ammontare, dobbiamo determinare il valore di QCP, intersecando
la curva di domanda con la curva (orizzontale) di costo marginale e risolvendo per la quantità.
Otteniamo a-bQ = c, da cui QCP=(a-c)/b.
L’area del triangolo EMAECP = {[(a-c)/b – (a-c)/2b] * [(a+c)/2 – c]} risulta, dopo pochi passaggi,
uguale a (a-c)2 / 8b.
ESERCIZIO 3
L’impresa Alfa, monopolista sul mercato, fronteggia la seguente curva di domanda: p = 360 – 4y,
dove p è il prezzo e y è la quantità prodotta. I costi dell’impresa sono dati dalla funzione: C = 2y2
a) Ottenete le funzioni dei ricavi marginali, dei costi medi e dei costi marginali del monopolista
MR = 360-8y
MC=4y
AC = 2y
6
b) Calcolate la quantità di equilibrio e il prezzo praticato dal monopolista.
MR=MC  360-8y = 4y  y* = 30
p* = 360- 120=240
c) Nel punto di equilibrio, l’elasticità è maggiore, minore o uguale a 1? Motivate la risposta senza
svolgere calcoli.
Sappiamo che il monopolista produce in corrispondenza del tratto elastico della curva di domanda:
in caso contrario non massimizzerebbe il suo profitto. Di conseguenza, l’elasticità è maggiore di 1.
d) Calcolate il profitto di equilibrio del monopolista e rappresentate l’area del profitto sul grafico.
 = py - 2y2 = 240*30 - 2*302 = 7200-1800 = 5400 (area in grassetto)
In alternativa, differenza MR e MC, rappresentata dall’ area del triangolo ABO.
MC
AC
P
360 A
E
240

B
MR
D
O
y
30
e) Calcolate il surplus del consumatore e il surplus totale dell’economia nel punto di equilibrio.
Surplus consumatore = area compresa fra la curva di domanda e il prezzo di mercato =
[(360-240) 30] / 2 = 1800
Surplus complessivo = surplus produttore + surplus consumatore = 5400+1800 = 7200
f) Supponete ora che il monopolista possa attuare una discriminazione di prezzo del primo ordine.
Definite il concetto di discriminazione di prezzo del primo ordine. Quale sarebbe la quantità di
equilibrio in questo caso?
7
La discriminazione di prezzo di primo ordine è una pratica che consente all’impresa di vendere
ciascuna unità esattamente al prezzo a cui i consumatori sono disposti a pagarla.
P= MC  360-4y=4y y*=45
ESERCIZIO 4
L’impresa EroGas&C. è l’unica fornitrice di metano del Varesotto e il rag. Vincenzi, che la
gestisce, ha l’obiettivo di massimizzare i profitti dell’azienda.
I dati a sua disposizione riguardano la funzione di costo totale dell’impresa:
TC (x) = 4x
e la domanda di mercato di gas, espressa dall’equazione:
P (x) = 40 – 2x
Dove x è il quantitativo di metano espresso in metri cubi e P è il suo prezzo al metro cubo.
a) Quale quantità di metano il rag. Vincenzi deve stabilire venga erogata dall’impresa?
Poniamo la condizione di ottimo MR=MC,con MR=40-4x (funzione di domanda lineare) e
MC=4, da cui xmon = 9 (e Pmon =22).
b) Rappresentate nel grafico sottostante la situazione di equilibrio monopolistico, indicando la
funzione di domanda (D), quella di costo marginale (MC) e quella di ricavo marginale (MR), con le
loro relative intercette e coefficienti angolari.
P
Pmon = 22
Emon
MR
D
Ecp
MC=4
A
-4
xmon=9 10
-2
xcp=18
20
c) Calcolate i profitti di monopolio dell’impresa.
Πmon=TR-TC=198-36=162
8
x
d) Ritenete che il livello di gas erogato sia socialmente efficiente ? Motivate la risposta.
Il livello di gas erogato socialmente efficiente – che massimizza il surplus sociale - risulta quello di
concorrenza perfetta; l’attuale situazione di monopolio, invece, determina una perdita secca pari
all’area del triangolo AEmonEcp. Essa scaturisce dal fatto che i metri cubi di gas comprese tra la
quantità erogata in monopolio e quella erogabile in concorrenza perfetta sarebbero acquistate dai
consumatori ad un prezzo superiore al loro costo di produzione.
e) Supponete ora che la Provincia di Varese decida di imporre all’EroGas&C. un prezzo tale da
massimizzare il benessere sociale. Determinate, in questo caso, prezzo e quantità di gas erogato, ed
i relativi profitti dell’impresa.
Il prezzo fissato dall’autorità pubblica sarà quello di concorrenza perfetta, determinato da P=MC,
per cui Pcp=4; a tale prezzo la quantità domandata sale a xcp=18 e i profitti dell’impresa sono nulli
(Πcp =0).
f) Come cambierebbe la situazione se l’impresa di distribuzione del gas fosse in grado di
discriminare perfettamente i propri clienti? Rispondete confrontando livelli di produzione e profitti
dell’impresa perfettamente discriminante con quelli calcolati ai punti c) ed e).
Se l’EroGas potesse discriminare perfettamente, allora produrrebbe una quantità pari a xcp=18,
applicando ad ogni consumatore il proprio prezzo di riserva ed ottenendo Πdp =18*(40-4)/2=324>
Πmon =162> Πcp =0.
In tal caso abbiamo ancora ottenuto una situazione socialmente efficiente, perché l’impresa è
riuscita ad assorbire nei profitti tutto il surplus di cui i consumatori godevano.
ESERCIZIO 5
Le Ferrovie Nord detengono il monopolio dei viaggi Milano-Castellanza. La curva di costo totale è
C  100 Q
mentre la curva di domanda inversa è
p  500  Q
dove p è il prezzo del biglietto (espresso in centesimi).
a)
Qual è il prezzo scelto dalle Ferrovie Nord al fine di massimizzare i profitti?
MC= 100
MC=MR cioè 100= 500-2Q Q*= 200
p*= 500-200= 300
9
Rappresentate graficamente l’equilibrio di monopolio nel grafico sottostante.
p
500
p*
E
100
MC
MR
D
Q
Q*
b)
Quale sarà il livello di profitti ottenuti in equilibrio?
= 300*200 – 100*200 = 200*200 = 40000
I clienti delle Ferrovie Nord e la regione Lombardia sono scontenti del servizio. Per aumentare la
loro soddisfazione, le
Ferrovie
Nord
considerano la
possibilità di
un investimento
nell’ammodernamento dei treni. Grazie a tale investimento, le Ferrovie Nord possono vedere la loro
domanda aumentata a p=1100-Q, mentre i costi di produzione rimangono invariati.
c)
Disegnate lo spostamento della curva di domanda nel grafico sottostante
p
1100
500
MC
Q
d)
Calcolate il nuovo prezzo e quantità di equilibrio, e i profitti corrispondenti, nel caso le
Ferrovie Nord decidano di investire nell’ammodernamento dei treni.
10
1100 – 2Q= 100
Q**= 500
e)
p**= 1100-500= 600 **= 600*500 – 100*500 = 250000
Date le risposte ai punti precedenti, qual è il costo massimo dell’investimento tale per cui le
Ferrovie Nord saranno effettivamente disposte ad investire?
Il costo massimo dell’investimento è dato dalla differenza tra i profitti nei due casi:
MAX C = 250000- 4000= 210000
f)
Nel prossimo anno accademico verrà terminata la costruzione delle Ferrovie Liuc. Le due
società preferiranno competere sulle quantità o sui prezzi? Motivate la risposta.
La configurazione di mercato diventa un duopolio: dal momento che la competizione sui
prezzi porta a profitti nulli, le due società preferiranno competere sulle quantità.
ESERCIZIO 6
Una nota casa farmaceutica tedesca elabora un vaccino anti-influenzale, la cui assunzione determina
una copertura contro tutte le possibili variabili di questa malattia nell’arco dei dieci anni successivi
alla vaccinazione. Per tutta la durata del brevetto l’impresa farmaceutica può considerarsi
monopolista rispetto alla domanda di questo bene, dato che i comuni vaccini non garantiscono una
copertura superiore all’anno. L’impresa produce il farmaco in un unico impianto, che ha costi totali
di produzione pari a C(Y) = 100 + 8Y, mentre può scegliere di vendere il prodotto nel mercato
nazionale (in quantità yN ed applicando un prezzo PN) o all’estero (in quantità yE e prezzo PE), con
Y= yN+ yE.
a)
Date le funzioni di domanda indiretta nel mercato nazionale yN(PN) = 400/(PN)2 e nel
mercato estero yE(PE) = 1000/(PE)3, ricavate prezzi e quantità di equilibrio in entrambi i
mercati.
La condizione richiesta è simile a quella utilizzata per l’allocazione ottima della produzione. Se,
in quel caso, dovevamo uguagliare costi marginali differenti ad un’unica espressione del ricavo
marginale, adesso abbiamo un solo impianto che produce per due differenti mercati; cioè,
abbiamo uno stesso costo marginale da uguagliare ai ricavi marginali ottenuti da due diverse
funzioni di domanda.
Per prima cosa, quindi, dobbiamo calcolare le due funzioni inverse di domanda, da cui ricavare
le espressioni dei ricavi marginali.
11
Per il mercato nazionale abbiamo: (PN)2= 400 / yN, da cui PN = 20 / (yN)1/2
Calcoliamo i ricavi totali sul mercato nazionale TR N = PN * yN, = 20 / (yN)1/2 * yN, = 20(yN)1/2 e,
da qui, calcoliamo i ricavi marginali sul mercato nazionale MR N = d TR N / dyN, = 20*1/2 (yN) 1/2
= 10 / (yN) ½ .
Procediamo in maniera analoga per il mercato estero: (PE)3 =1000/yE, da cui PE=10 / (yN)1/3
Calcoliamo i ricavi totali sul mercato estero TR
E
= PE * yE, = 10 / (yE)1/3 * yE, = 10 (yE)2/3 e
calcoliamo i ricavi marginali sul mercato estero MR E = dTR E / dyE, = 10*2/3*(yE) -1/3
= 20 /[3 (yE)1/3 ].
I costi marginali risultano MC = dC(Y)/dY = 8.
Da MR N =MC abbiamo 10 / (yN) ½ = 8 da cui (yN) ½ =10/8 che, semplifiando ed elevando entrambi
i membri al quadrato, fornisce yN, = (5/4)2, cioè la quantità prodotta nel mercato
nazionale.
Il prezzo praticato in questo mercato è ricavato sostituendo il valore numerico di yN, nella funzione
di domanda interna: PN = 20 / [(5/4)2] 1/2 = 20*4/5 = 16.
Da MR E =MC abbiamo 20 /[3 (yE)1/3 ] = 8 da cui (yE) 1/3 =20/3*8 che, semplificando ed elevando
entrambi i membri al cubo, fornisce yE, = (5/6)3
Come in precedenza, per trovare il prezzo applicato sui mercati esteri, bisogna sostituire il valore
numerico di yE nella relativa funzione di domanda: PE =10 / [(5/6) 3] 1/3 = 10*6/5 = 12.
b)Verificate che il monopolista applica un prezzo più elevato nel mercato a domanda più rigida.
Il secondo punto richiede di verificare la seguente relazione PN > PE  N < E.
Dobbiamo quindi calcolare i valori delle elasticità sul mercato nazionale ed estero, utilizzando la
consueta formula per il calcolo dell’elasticità (calcolo la derivata rispetto al prezzo nella funzione
di domanda ricavata al punto a e sostituisco i valori numerici di prezzi e quantità relativi ai singoli
mercati, anch’essi ottenuti come soluzione al primo punto).
N =
dy N PN
= 0,1953125*10,24 = 2.
dPN y N
E =
dy E PE
= 0,1447*20,736= 3.
dPE y E
Effettivamente il monopolista applica un prezzo più elevato nel mercato a domanda più rigida.
12