MATEMATICA - CLASSE TERZA
1 - OBIETTIVI DISCIPLINARI
acquisire la capacità di risolvere disequazioni intere e fratte di 2° grado e sistemi di disequazioni
conoscere il grafico di funzioni esponenziali, logaritmiche e goniometriche
collegare l'aspetto algebrico-analitico a quello grafico-geometrico
2 - LIVELLI MINIMI DI SUFFICIENZA
risolvere disequazioni intere e fratte di 1° e di 2° grado
risolvere semplici problemi sulle coniche (circonferenza, parabola)
conoscere la definizione di logaritmo
risolvere equazioni logaritmiche ed esponenziali elementari
risolvere espressioni goniometriche.
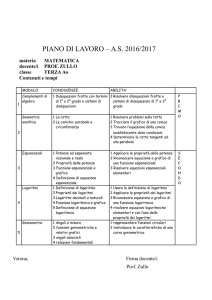
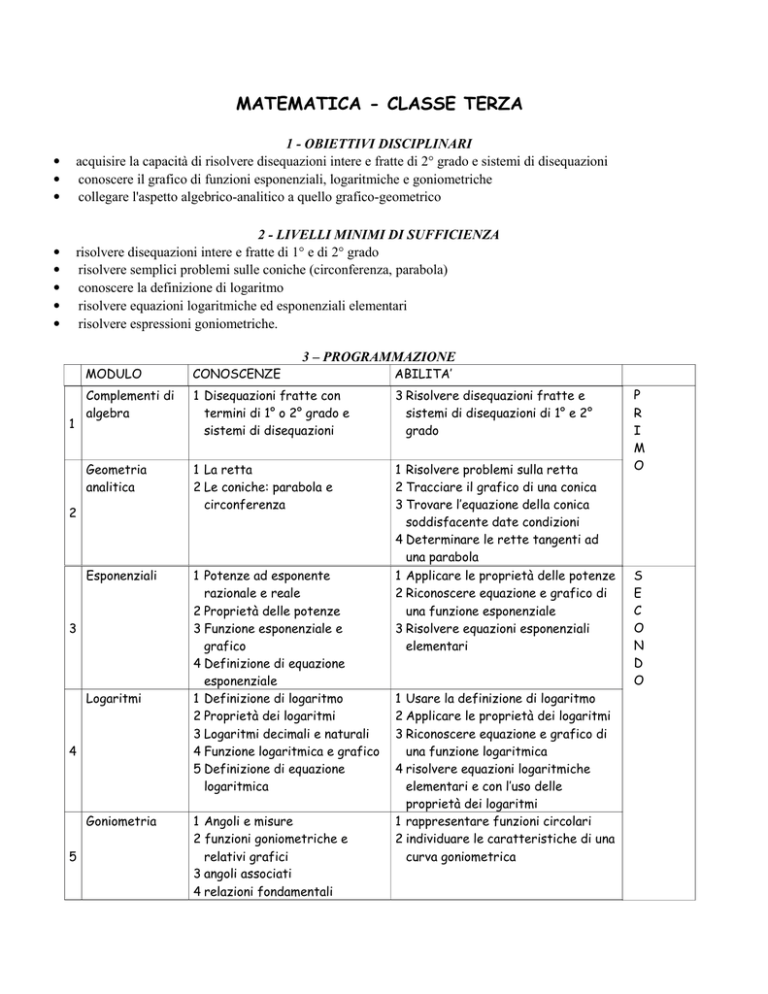
3 – PROGRAMMAZIONE
1
MODULO
CONOSCENZE
ABILITA’
Complementi di
algebra
1 Disequazioni fratte con
termini di 1° o 2° grado e
sistemi di disequazioni
3 Risolvere disequazioni fratte e
sistemi di disequazioni di 1° e 2°
grado
Geometria
analitica
1 La retta
2 Le coniche: parabola e
circonferenza
1 Risolvere problemi sulla retta
2 Tracciare il grafico di una conica
3 Trovare l’equazione della conica
soddisfacente date condizioni
4 Determinare le rette tangenti ad
una parabola
Esponenziali
1 Potenze ad esponente
razionale e reale
2 Proprietà delle potenze
3 Funzione esponenziale e
grafico
4 Definizione di equazione
esponenziale
1 Definizione di logaritmo
2 Proprietà dei logaritmi
3 Logaritmi decimali e naturali
4 Funzione logaritmica e grafico
5 Definizione di equazione
logaritmica
1 Applicare le proprietà delle potenze
2 Riconoscere equazione e grafico di
una funzione esponenziale
3 Risolvere equazioni esponenziali
elementari
2
3
Logaritmi
4
Goniometria
5
1 Angoli e misure
2 funzioni goniometriche e
relativi grafici
3 angoli associati
4 relazioni fondamentali
1 Usare la definizione di logaritmo
2 Applicare le proprietà dei logaritmi
3 Riconoscere equazione e grafico di
una funzione logaritmica
4 risolvere equazioni logaritmiche
elementari e con l’uso delle
proprietà dei logaritmi
1 rappresentare funzioni circolari
2 individuare le caratteristiche di una
curva goniometrica
P
R
I
M
O
S
E
C
O
N
D
O