FRIGORIFERI E POMPE DI CALORE

FRIGORIFERI E POMPE DI CALORE
Abbiamo visto nei precedenti capitoli che la conversione di calore in lavoro in una macchina
bitermica reversibile ha una efficienza che dipende dalla differenza tra le temperature assolute dei
serbatoi (termostati) tra i quali si fa lavorare la macchina.
Essendo quella del termostato costituito dall’ambiente esterno la temperatura più bassa che abbiamo
a disposizione, tutte le nostre macchine lavoreranno tra la temperatura Tsup della sorgente “calda” ed
una Tinf pari a quella dell’ambiente, con un rendimento che, (soltanto!) nel caso della macchina di
Carnot inserita in un ciclo bitermico reversibile, può scriversi:
.
η = 1−
Tinf
Tsup
1500 K
600 K
Q1
375 K
Q1
Q1
C
C
C
L = 0,5 Q1
L = 0,8 Q1
L = 0,2 Q1
300 K
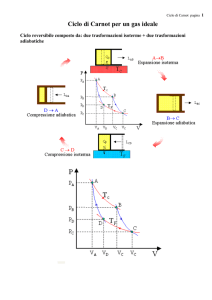
Nella figura, tre macchine di Carnot lavorano tra altrettanti serbatoi a diverse temperature e
l’ambiente, considerato come un termostato alla temperatura costante di 300 K.
Riferendosi ai valori assoluti di L e Q, è possibile vedere come la stessa quantità di calore Q1
estratta dai diversi serbatoi venga convertita in quantità di lavoro diverse in funzione della
temperatura alla quale Q1 è disponibile.
Nel primo caso ben l’80% del calore Q1 è convertito in lavoro meccanico, mentre il restante 20%,
scaricato nell’ambiente, diventa inutilizzabile per la produzione di ulteriore lavoro; nell’ultimo caso
la convertibilità di Q1 in lavoro meccanico è appena del 20%, mentre l’80% diviene inservibile.
Solo un ipotetico termostato a temperatura infinita potrebbe assicurare la conversione totale di Q1
in lavoro, condizione manifestamente impossibile perché comporterebbe anche Q2 = Q1 - L = 0 e
pertanto la macchina, utilizzando di fatto solo una sorgente, sarebbe monoterma.
Ne abbiamo concluso che il lavoro ciclico massimo ricavabile da una generica quantità di calore Q
disponibile alla generica temperatura Ti (con Ti > Tamb), si può ottenere mediante una macchina di
Carnot operante tra Ti e Tamb.
1
Poniamoci adesso il problema inverso: è possibile ottenere una determinata quantità di Energia
sotto forma di Calore partendo da Energia sotto forma di Lavoro meccanico?
Questa conversione è certamente possibile, visto che il Lavoro meccanico può essere convertito in
qualsiasi altra forma di Energia.
In figura, l’energia elettrica contenuta in una batteria di accumulatori (energia che abbiamo
identificato come lavoro meccanico) si trasforma in calore sulla resistenza elettrica con un
rendimento di conversione pari ad uno.
L
Tamb
Q = L
Pertanto è evidente che, partendo da una certa quantità di Lavoro, è possibile ottenere una identica
quantità Calore a qualsiasi temperatura, sempre però superiore alla temperatura dell’ambiente, in
questo caso infatti avremmo reso il Calore totalmente inutilizzabile.
Teoricamente, se si disponesse di un sistema perfettamente isolato dal punto di vista termico, si
potrebbe portare il sistema a temperature elevatissime, dalle quali si potrebbe sempre riottenere, per
mezzo di una macchina, praticamente tutto il lavoro speso.
Ottenere Calore a bassa temperatura (ma comunque superiore a quella ambiente) comporta la
perdita della possibilità di riconvertire gran parte del Calore in Lavoro e quindi la perdita di una
notevole quantità di Energia Utilizzabile.
Vi è però un’altra possibilità di ottenere Calore a bassa temperatura senza perdita di Energia
Utilizzabile.
L’ambiente infatti è un termostato che possiede una enorme (praticamente infinita) quantità di
Calore, essa però è disponibile alla temperatura stessa dell’ambiente e pertanto non è utilizzabile
per ottenere Lavoro ciclico mediante una Macchina di Carnot.
Tuttavia, utilizzando una Macchina che lavori a ciclo inverso, sottraendo Calore all’ambiente e
fornendo alla Macchina la sufficiente quantità di Lavoro meccanico, è possibile produrre una stessa
quantità di calore Q1 alla temperatura desiderata.
Nella figura tre macchine di Carnot producono il Calore Q1 in altrettanti termostati posti a tre
diverse temperature.
Nella Macchina più a destra il Calore Q1 è composto per l’80% di calore gratuito prelevato
dall’ambiente e “riqualificato” a 375 K grazie all’apporto di Lavoro meccanico nella misura del
rimanente 20% .
2
1500 K
Q1
600 K
375 K
Q1
Q1
C
C
C
L = 0,5 Q1
L = 0,8 Q1
L = 0,2 Q1
300 K
Sempre con l’avvertenza di considerare Calore e Lavoro in valore assoluto, osserviamo che la prima
Macchina produce lo stesso calore Q1 prodotto dalla terza Macchina, ma lo fa quasi tutto a spese del
lavoro meccanico, mentre il contributo dell’ambiente si limita ad un 20%.
Se ne deduce che la produzione del calore Q1 mediante ”innalzamento termodinamico” di una certa
quantità di calore prelevata gratuitamente dall’ambiente è tanto più conveniente quanto più bassa è
la “spesa” in termini di Energia meccanica e quindi quanto più bassa è la temperatura alla quale
vogliamo disporre del calore Q1.
Si noti che questo “innalzamento termodinamico” è sostanzialmente diverso dalla trasformazione
diretta di lavoro in calore, in quanto quest’ultima operazione comporta un aumento dell’Entropia
dell’Universo tanto più grande quanto più piccola è la differenza tra la temperatura alla quale il
Calore è reso disponibile e la temperatura dell’Ambiente.
Ricordiamo infatti che la perdita della possibilità di produrre lavoro ciclico, o Lavoro Perduto, è
misurata proprio dalla variazione di Entropia dell’Universo moltiplicata per la temperatura di
riferimento dell’ambiente.
L Perd = Tamb ∆S tot
Nel nostro caso non vi è alcuna irreversibilità, né nella macchina, né nell’ambiente, infatti la
quantità di calore Q1 può sempre essere impiegata in una macchina a ciclo diretto per recuperare il
lavoro meccanico precedentemente impegnato.
Osserviamo ora che in una macchina che opera a ciclo diretto, il Calore si trasforma in lavoro
andando spontaneamente dalle temperature elevate che troviamo nelle sorgenti geotermiche o che
realizziamo nelle caldaie, nei reattori nucleari, etc., verso la temperatura più bassa che abbiamo a
disposizione e che è necessariamente quella dell’ambiente.
Invece, una macchina che opera a ciclo inverso costringe il calore a comportarsi in contrasto a
quanto gli è imposto dal Secondo Principio della Termodinamica nella formulazione del Postulato
di Clausius ed infatti lo forza ad andare da temperature più basse verso temperature più alte.
3
Ciò significa che non ha senso pensare ad una macchina a ciclo diretto che non abbia come
riferimento inferiore l’ambiente, mentre una macchina a ciclo inverso può avere l’ambiente esterno
come riferimento superiore o come riferimento inferiore.
T1 > Tamb
T1 > Tamb
Tamb
Q1
Q1
Q1
C
C
L
Q2
Q2
Tamb
Tamb
Ciclo diretto
C
L
L
Q2
T2 < Tamb
Cicli inversi
Osservando i due casi di ciclo inverso notiamo che la macchina può fornire ad un termostato avente
una temperatura più alta di quella dell’ambiente, il calore prelevato dall’ambiente, sommato
all’energia meccanica impegnata dalla macchina stessa, mentre nel secondo caso la macchina
scarica nell’ambiente il calore sottratto ad un ipotetico termostato avente una temperatura più bassa
di quella dell’ambiente, sempre sommandolo all’energia meccanica richiesta dalla macchina.
Tamb
T1 > Tamb
Q1
Q1
C
Q2
C
L
L
Q2
T2 < Tamb
Tamb
4
Se al posto dei due termostati immaginiamo due sistemi a capacità termica finita, perfettamente
isolati termicamente, ci rendiamo conto che, mediante la prima macchina possiamo “pompare
calore” all’interno di un sistema la cui temperatura andrà via via crescendo rispetto a quella
dell’ambiente, mentre con la seconda macchina possiamo sottrarre calore ad un sistema la cui
temperatura andrà via via diminuendo rispetto a quella dell’ambiente.
Per quanto si è osservato sopra, è evidente che queste operazioni impegneranno tanto più lavoro
meccanico quanto maggiore andrà facendosi la differenza di temperatura tra ciascuno dei sistemi e
l’ambiente esterno.
Poiché l’esistenza dei sistemi termicamente isolati è puramente teorica, nella realtà si avranno
“fughe” di calore verso l’esterno nel primo caso ed apporti indesiderati nel secondo; si giungerà
quindi nella pratica ad una situazione di equilibrio tra i flussi di calore entranti/uscenti e le
dispersioni (positive e negative) verso l’ambiente esterno; il valore di temperatura di regime
dipenderà dalla potenza a disposizione della macchina.
Parleremo quindi di POMPE DI
CALORE nel primo caso e di
FRIGORIFERI nel secondo caso.
Tamb
Si osservi che la distinzione tra pompa di
calore e frigorifero è puramente operativa,
infatti nei due casi la macchina “non sa” se
stia funzionando come l’una o come l’altro.
Q1
C
Q1
Q2
C
L
L
Nella pratica, ove le macchine fossero
progettate per funzionare esclusivamente
da Pompa di calore o da Frigorifero, le loro
caratteristiche costruttive potrebbero essere
diverse per adattarsi meglio ai diversi
campi di temperatura di funzionamento.
Nel caso di macchine progettate per la
produzione del caldo e/o del freddo negli
stessi campi di temperatura (pompe di
calore invertibili) si tratterà esattamente
della stessa macchina usata in condizioni
esterne diverse.
Q2
Tamb
Pompa di calore
Frigorifero
E’ opportuno sottolineare che, mentre esistono moltissimi altri modi per produrre calore a
temperatura superiore a quella dell’ambiente, che non fanno uso del “sollevamento termodinamico“
tramite una macchina a ciclo inverso, la produzione del freddo (in maniera continuativa) è possibile
soltanto attraverso l’uso di una macchina (funzionante a ciclo inverso o mediante reazioni chimiche
di assorbimento).
5
In analogia con quanto si è fatto per la macchina a ciclo diretto, per la quale abbiamo definito
“Rendimento” il rapporto tra quanto vogliamo ottenere (il Lavoro meccanico) e la spesa sostenuta
(il Calore fornito dalla sorgente ad alta temperatura):
η=
L Q1 − Q 2
Q
=
= 1− 2
Q1
Q1
Q1
(Carnot ) ηC = 1 −
T2
T1
le caratteristiche di funzionamento di una macchina inversa si definiscono attraverso un coefficiente
detto COP (Coefficient of Performance) che rappresenta sempre il rapporto tra quanto si vuole
ottenere e quanto si deve spendere per ottenerlo.
A differenza della macchina a ciclo diretto però sono ora possibili due diversi tipi di COP:
-
uno per la Pompa di Calore, che esprime il rapporto tra le Calorie prodotte (ovvero il
calore “pompato” al termostato superiore) ed il lavoro speso per ottenere questo calore
utilizzato per riscaldamento (Heating):
COPH =
-
Q1
Q1
=
L Q1 − Q 2
(Carnot ) COPHC =
T1
T1 − T2
uno per il Frigorifero, che esprime il rapporto tra le Frigorìe prodotte (ovvero il calore
COPR =
Q2
Q2
=
L Q1 − Q 2
(Carnot ) COPRC =
T2
T1 − T2
estratto dal termostato inferiore) ed il lavoro speso per estrarre questo calore utilizzato
per raffreddamento (Refrigerating):
Un’altra differenza con la macchina a ciclo diretto, il cui rendimento non potrà mai essere maggiore
di uno perché il lavoro prodotto non potrà mai essere maggiore del calore estratto dal termostato
superiore, consiste nel fatto che ambedue i COP potranno essere maggiori di uno, essi infatti
tendono ad infinito quando le temperature delle sorgenti si avvicinano ed il lavoro necessario per
pompare o per estrarre calore tende a zero.
Si può osservare ancora che il COPH di una pompa di calore è pari all’inverso del rendimento della
corrispondente macchina diretta, mentre il COPR di un frigorifero lo diventa solo se la differenza tra
le temperature di funzionamento sono molto piccole e quindi 1/η >> 1.
COPH =
1
η
COPR =
1
−1
η
Pertanto la stessa macchina di Carnot, se venisse usata in ciclo inverso di riscaldamento per
mantenere un ambiente a 30 °C mentre l’ambiente esterno si trova 0 °C avrebbe:
COPHC = (273,15+30)/30 = 10,105
6
mentre se venisse usata in ciclo inverso di refrigerazione per mantenere un ambiente a 0 °C mentre
l’ambiente esterno si trova a 30 °C avrebbe:
COPRC = 273,15/30 = 9,105
La macchina, usata in ciclo diretto, avrebbe infatti un rendimento molto basso, pari a:
ηC = 30/(273,15+30) = 0,09896
SUPERIORITA’ DEL CICLO DI CARNOT INVERSO
Per una macchina politermica reversibile funzionante in un ciclo inverso vale la relazione di
Clausius, che può essere scritta, spezzando l’integrale esteso al ciclo nella somma algebrica di due
integrali:
∫
δQ
=0=
T
∫
ricevuto
| δQ r |
−
Tri
+ entrante
∫
ceduto
| δQ c |
Tci
− uscente
il primo dei quali è esteso a tutti i tratti infinitesimi del ciclo in cui il calore (positivo) viene fornito
al sistema dalle infinite sorgenti esterne, mentre il secondo è esteso a tutti i tratti infinitesimi del
ciclo in cui il calore (negativo) viene ceduto dal sistema alle infinite sorgenti esterne.
Assumendo che la corrispondente macchina di Carnot sia quella che lavora tra la temperatura T2C
scelta come la temperatura più alta tra quelle alle quali il calore viene ricevuto dal sistema lavorante
e la temperatura T1C scelta come la temperatura più bassa tra quelle alle quali il calore viene ceduto
dal sistema lavorante:
T2C ≥ Tri
T1C ≤ Tci
Sostituendo le due temperature della macchina di Carnot, alle diverse temperature del ciclo si ha:
0>
| δQ c |
| δQ r |
− ∫
ricevuto T2 C
ceduto T1C
0>
∫
| Q 2 | | Q1 |
−
T2 C
T1C
| Q 2 | | Q1 |
<
T2 C
T1C
( più piccolo ) ( più grande )
| Q 2 | T2C
<
| Q1 | T1C
1
1
<
|Q |
T
1− 2
1 − 2C
| Q1 |
T1C
; 1−
;
T
| Q2 |
> 1 − 2C
T1C
| Q1 |
T1C
| Q1 |
<
| Q1 | − | Q 2 | T1C − T2C
7
Si conclude pertanto che una qualsiasi macchina politermica reversibile funzionante come pompa
di calore ha un Coefficiente di performance minore di quello della corrispondente macchina
funzionante con un ciclo di Carnot inverso.
COPH < COPHCarnot
E ricordando che COPR = COPH−1 è evidente che sarà anche:
COPR < COPRCarnot
Graficamente, rappresentando su di un diagramma T,S un ciclo
motore politermico reversibile, è sempre possibile individuare
il ciclo di Carnot corrispondente che è delimitato dalla isoterma
T1C corrispondente alla temperatura più alta del tratto ABC
lungo il quale il ciclo assorbe calore, dalla temperatura più
bassa del tratto CDA lungo il quale il ciclo cede calore ed
ovviamente dalle due adiabatiche tangenti al ciclo nei punti A e
C in cui il ciclo stesso non scambia calore.
T
T1C
B
A
+
T2C
D
−
C
S
In un ciclo motore non c’è alcuna difficoltà ad individuare il
ciclo di Carnot corrispondente perché il calore entra sempre
alla temperatura più alta del ciclo ed esce sempre alla
temperatura più bassa del ciclo.
Osserviamo cosa succede se proviamo ad invertire il senso del ciclo politermico reversibile: ora il
calore entra alla temperatura più bassa ed esce alla temperatura più alta.
Accade un fatto apparentemente strano: le temperature dei punti A e C sono contemporaneamente le
temperature del punto più alto al quale il calore viene ricevuto e del punto più basso al quale il
calore viene ceduto.
T
Se ne deduce che il corrispondente ciclo inverso di Carnot
(frigorifero o pompa di calore) non esiste!
D
T1C A
T2C
−
C
Ciò potrebbe essere dovuto alla particolare forma simmetrica
del ciclo ABCD, infatti, se proviamo a modificare la forma del
ciclo notiamo che ora è possibile distinguere i due punti A e C
e disegnare un ciclo di Carnot.
B
+
S
8
T
T1c
D
T1C
−
T2C
A
Q1
L
C
Q2
T2c
L
C
B
+
T1c
Q1
C
Q2
S
T2c
Ci accorgiamo però che la temperatura T1C corrisponde alla temperatura più
alta alla quale il calore viene ricevuto dalla macchina (tratto ABC) e non
ceduto, come dovrebbe succedere nella macchina inversa rappresentata
accanto al ciclo.
Così anche T2C corrisponde alla temperatura più bassa alla quale il calore viene
ceduto dalla macchina (tratto CDA) e non ricevuto, come dovrebbe
succedere se la macchina fosse la macchina inversa rappresentata accanto al
ciclo.
Pertanto la macchina di Carnot corrispondente al nostro ciclo inverso
politermico reversibile è un motore e non un frigorifero o una pompa di
calore, infatti la sua temperatura più alta è quella alla quale il calore entra
nella macchina, proprio come avviene in una macchina diretta.
Consideriamo allora il significato fisico di quanto abbiamo osservato sopra immaginando di avere a
che fare con un frigorifero:
Il tratto ABC in cui il calore viene ricevuto o, lungo il quale vengono prodotte le frigorie,
rappresenta la parte fredda della macchina, mentre il tratto CDA è la parte calda della macchina.
Nel caso del ciclo simmetrico esiste un punto della parte fredda della macchina che ha la stessa
temperatura di un punto della parte calda.
Poiché Carnot deve scegliere due sole temperature con il criterio che abbiamo accennato,
semplicemente non esiste un frigorifero di Carnot corrispondente.
Ancor più evidente è il secondo caso in cui alcune temperature della parte fredda sono addirittura
più alte di altre della parte calda.
In questo caso Carnot non solo rinunzia all’idea di lavorare come frigorifero, ma, trovandosi nelle
condizioni di farlo, si costruisce una macchina che opera in maniera diretta tra una sorgente
costituita dalla parte più calda della parte “fredda” del frigorifero politermico e la parte più fredda
della parte “calda” .
9
E’ evidente allora il significato fisico di quello che abbiamo osservato fin qui:
La condizione di esistenza di un frigorifero (o di una pompa di calore) comporta che la sua
parte “fredda” e la sua parte “calda” non abbiano punti in comune.
Per ottenere questa condizione occorre e basta che la parte calda e la parte fredda siano collegate da
due tratti di trasformazione in cui non vi sia scambio di
calore, quindi da due adiabatiche (o da due
D
T
trasformazioni non reversibili).
In figura è rappresentato un ciclo politermico reversibile
C’
in cui il calore viene assorbito nel tratto A’BC e ceduto
nel tratto C’DA. I due tratti non hanno alcun punto in
T1C
comune e la temperatura più alta alla quale il calore
A
viene assorbito T2C è inferiore alla temperatura più
CARNOT
T2C
bassa T1C alla quale il calore viene ceduto.
C
E’ possibile così identificare la macchina inversa di
Carnot che lavora tra le temperature T1C e T2C con un
COP evidentemente superiore a quello del ciclo
A’
politermico come è evidente dal grafico.
B
Dal grafico infatti si nota che la macchina di Carnot
assorbe molto più calore (produce molte più frigorìe)
+
S
del ciclo politermico, richiedendo un lavoro molto più
piccolo.
−
−
+
CICLO JOULE INVERSO : FRIGORIFERO AD ARIA
T
D
T1C A
Espansore Compressore
Carnot
T2C
C
B
S
Nelle figure sono rappresentati il ciclo frigorifero di Joule e lo schema della macchina che lo
realizza.
Un fluido (aria) considerato gas perfetto viene compresso adiabaticamente a partire dal punto C,
raffreddato nello scambiatore superiore a pressione costante (tratto DA) e fatto quindi espandere
adiabaticamente fino al punto B. La trasformazione isobara BC riporta il fluido nelle condizioni
iniziali.
E’ facile individuare il Ciclo di Carnot corrispondente, che lavora tra le temperature T2C e T1C il cui
COP è evidentemente più alto di quello del ciclo Joule.
10
Spostando l’adiabatica CD verso destra, la
temperatura del punto C tenderebbe ad
aumentare, mentre l’area del ciclo di
Carnot tenderebbe a restringersi.
Quando la temperatura del punto C
raggiunge quella del punto A, la macchina
inversa di Carnot non esiste più.
E’ anche facile rendersi conto che,
aumentando ancora la temperatura del
punto C, il ciclo di Carnot si
ripresenterebbe in forma invertita, con
T2C>T1C e quindi sotto forma di ciclo
motore come abbiamo notato sopra.
D
T
T2C A
T1C
Carnot
C
B
S
Calcolo del COP del ciclo Joule inverso ideale, funzionante con un gas perfetto:
1) Compressione isoentropica da C a D : L’CD = JD − JC = cp (TD − TC), ed essendo SC = SD
k −1
⎞ k
⎛P
TD = TC ⎜⎜ D ⎟⎟
⎝ PC ⎠
=
k −1
TC rP k
dove L’ è il lavoro del compressore ed rp = (PD / PC) è il rapporto di compressione.
2) Raffreddamento isobaro del gas nello scambiatore superiore. Durante lo scambio di calore dal
sistema verso l’esterno, l’entalpia, la temperatura e l’entropia del gas diminuiscono.
QDA = JA − JD = cp (TA − TD)
⎛T ⎞
SA − SD = c P ln⎜⎜ A ⎟⎟
⎝ TD ⎠
PA = PD
3) Espansione isoentropica da A a B. L’AB = JB − JA = cp (TB − TA), ed essendo SA = SB
⎛P
TA = TB ⎜⎜ A
⎝ PB
⎞
⎟⎟
⎠
k −1
k
=
k−1
TB rP k
4) Produzione di Frigorìe nello scambiatore dove assorbe calore in un processo isobaro durante il
quale, l’entalpia, la temperatura e l’entropia del gas crescono.
⎛T ⎞
SC − SB = c P ln⎜⎜ C ⎟⎟
QBC = JC − JB = cp (TC − TB)
PB = PC
⎝ TB ⎠
Il COP del ciclo Joule inverso è pertanto:
COP =
Q BC
Frigorie prodotte
1
1
1
1
= k −1
=
=
=
=
k
1
−
c p (TD − TA )
Lavoro speso
Q DA − Q BC Q DA
−1
k
− 1 (TC − TB ) rP k
− 1 rP − 1
Q BC
c p (TC − TB )
(TC − TB )
che si poteva scrivere subito, perché essendo ηJoule = 1 −
1
k −1
rP k
si ha : COPJoule =
1
ηJoule
−1
11