ESERCIZI SULLA PARABOLA
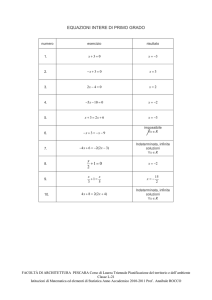
1. Date le seguenti equazioni di parabole , determinare concavità, asse di simmetria e vertice:
Concavità
Asse di
simmetria
Coordinate
vertice
y = x2 − 4x + 3
U verso l’alto
x=2
V ( 2;3)
y = − x2 + 6x + 3
I verso il basso
x=3
V (3;12)
y = − x2 + 2x
I verso il basso
x =1
V (1;1)
y = − x2 + 4
I verso il basso
x=0
V (0;4)
y = x2 + 4
U verso l’alto
x=0
V (0;4)
y = 4x 2
U verso l’alto
x=0
V (0;0)
y = 4x2 − 8
U verso l’alto
x=0
V (0;−8)
equazione
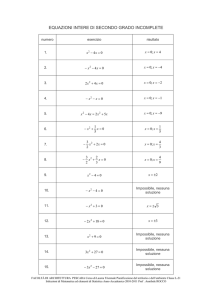
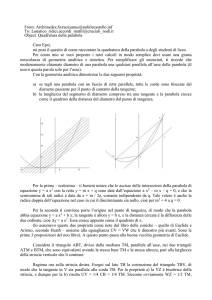
2. Tracciare il grafico delle seguenti parabole :
A)
y = 4x2 − 8x + 1
B)
y = − x2 − 2x + 1
C)
y = − x 2 + 3x
D)
y = − x2 + 4
E)
y = − x2 − 4
y = − x2 − 2x + 1
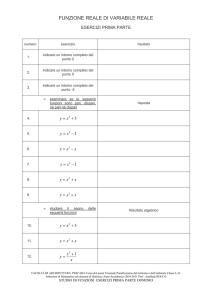
3. Scrivere l’equazione della parabola passante per i tre punti sotto indicati:
lettera
segmento di estremi
Equazione della parabola
A
A(0;0) B (1;5) C ( −1;−3)
y = x2 + 4x
B
A(0;6) B (1;5) C ( −3;−3)
y = − x2 + 6
C
A(1;8) B (−1;0) C ( −2;−1)
y = x2 + 4x + 3
D
A(1;3) B (−1;9) C ( 2;6)
y = 2 x 2 − 3x + 4
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 1 di 6
ESERCIZI SULLA PARABOLA
4. Scrivere l’equazione della parabola passante per il punto e il vertice sotto indicati:
lettera
coordinate del
punto P
coordinate del
vertice V
Equazione della parabola
A
A(0;0)
V ( 2;4)
y = − x2 + 4x
B
A(1;4)
V (0;6)
y = −2 x 2 + 6
C
A(1;−2)
V (3;−6)
y = x2 − 6x + 3
D
A( −1;−9)
V (1;7)
y = −2 x 2 + 8 x + 1
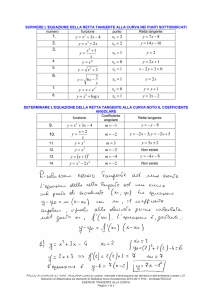
5. verificare se la retta è esterna, secante o tangente alla parabola e trovare i punti di contatto:
Equazione della parabola
Risposta
secante ,
tangente,
esterna
Coordinate eventuali
punti di contatto
y+x=0
y = x 2 + 3x
SECANTE
P(0;0) ∨ Q( −4;+4)
B
y − x = 0
y = − x 2 − 3x
SECANTE
P(0;0) ∨ Q( −4;−4)
C
2x + y = 0
y = −x2 − 3
ESTERNA
D
2x + y = 0
y = − x2 − 1
TANGENTE
P(1;−2)
E
2x + y = 0
y = − x2 + 3
SECANTE
P( −1;2) ∨ Q (3;−6)
F
y=0
y = − x2 + 9
SECANTE
P( −3;0) ∨ Q ( +3;0)
G
y = −5
y = x2 + 4x
ESTERNA
H
y − 6x − 4 = 0
y = x2 + 4x + 5
TANGENTE
lettera
equazione della
retta
A
P(1;10)
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 2 di 6
ESERCIZI SULLA PARABOLA
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 3 di 6
ESERCIZI SULLA PARABOLA
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 4 di 6
ESERCIZI SULLA PARABOLA
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 5 di 6
ESERCIZI SULLA PARABOLA
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 6 di 6