Geometrie non euclidee
1. Il metodo assiomatico
La matematica moderna è un sistema ipotetico-deduttivo. Ciò significa che la verità di ogni proposizione è dedotta con
un procedimento logico da ipotesi, che sono altre proposizioni assunte come vere. Tale procedimento si chiama
dimostrazione; le proposizioni dimostrate si chiamano teoremi. Il punto importante è che in una dimostrazione è
obbligatorio attenersi a certe regole del ragionamento logico. Perciò una dimostrazione non consiste nello "svelare l'evidenza
di una verità" usando argomenti più o meno convincenti, il che avrebbe a che fare più con l'abilità retorica che con la logica. La
dimostrazione di un teorema consiste invece nel far vedere che esso è una conseguenza logica necessaria di proposizioni
precedenti. Ma siccome queste a loro volta devono essere dimostrate da altre e queste da altre ancora, se non si vuole andare
all'indietro all'infinito è necessario premettere a ogni sistema deduttivo un certo numero di proposizioni iniziali, dette
postulati o assiomi, per la cui verità non si richiede dimostrazione.
Il metodo assiomatico consiste nell'applicare agli assiomi le regole della deduzione logica, per ricavarne altre proposizioni,
la cui verità è garantita dalla corretta applicazione di quelle regole. Al contrario la verità dei postulati non ha bisogno di
nessuna giustificazione, neanche intuitiva: la matematica moderna ha infatti abbandonato l'idea che gli assiomi debbano
essere accettati come veri perché sarebbero di per sé evidenti, in virtù di considerazioni intuitive o empiriche. Dal punto di
vista logico, la scelta degli assiomi è del tutto arbitraria, purché essi siano compatibili, cioè non in contraddizione tra di loro.
Se infatti ci fosse una contraddizione di partenza, qualunque proposizione potrebbe essere dimostrata: dunque si potrebbe
dimostrare qualunque proposizione insieme con la sua contraria.1
Oltre a essere compatibili, gli assiomi non devono contenere più di quanto è necessario per dedurne tutte le conseguenze. In
particolare nessun assioma deve essere a sua volta deducibile dagli altri assiomi; si dice che gli assiomi devono essere
indipendenti. Sulla questione della compatibilita e della indipendenza torneremo nei prossimi paragrafi, a proposito di
particolari sistemi assiomatici della geometria.
Le proposizioni della matematica sono degli enunciati riguardanti concetti del sistema deduttivo al quale si riferiscono. Per
esempio le proposizioni della geometria stabiliscono correlazioni tra punti, rette, piani, segmenti, angoli, superfici e così via;
inoltre vi compaiono termini come "uguale", "maggiore", "perpendicolare" e molti altri. Perché un enunciato sia comprensibile, è
necessario che i termini che vi compaiono siano definiti. Ma un termine viene definito per mezzo di altri termini; per esempio
per definire "segmento" si devono conoscere i termini "punto", "retta" e "fra". Perciò in un sistema assiomatico non avremo
soltanto un certo numero di postulati iniziali, ma anche un elenco iniziale di termini primitivi; "primitivo" significa che non
si definisce. Per meglio dire, i termini primitivi sono implicitamente definiti dagli assiomi. Per esempio "uno", "numero" e
"successivo" sono i termini primitivi della teoria dei numeri naturali e sono implicitamente definiti da quelli che ormai sono
riconosciuti come gli assiomi di Peano. In geometria "punto", "retta" e "piano" sono termini primitivi: i punti, le rette e i piani
sono implicitamente definiti come quelle cose (qualunque cosa siano!) per le quali sono veri i postulati. Così gli enti
fondamentali della geometria non possiedono di per sé nessun significato concreto o, per meglio dire, sono suscettibili di
più interpretazioni concrete diverse. Ciascuna di queste interpretazioni è un modello di geometria.
L'idea della definizione dei concetti primitivi per mezzo di assiomi è un'idea moderna, non anteriore al XIX secolo. Prima di
allora l'opinione comune è sempre stata che la geometria euclidea fosse una descrizione della realtà fisica, cioè che i teoremi
di geometria fossero un'illustrazione delle proprietà dello spazio fisico. Quest'ultimo, l'universo della comune esistenza,
avrebbe tutte le proprietà dello spazio tridimensionale euclideo. Secondo il "buon senso" implicito in tali convinzioni, peraltro
avvalorate dall'autorità dei filosofi da Platone a Kant, i postulati della geometria euclidea erano categorie a priori per l'interpretazione della realtà e gli enti geometrici possedevano un significato sperimentale. Questa concezione fu messa in crisi sia
dalle ricerche sulle geometrie non euclidee, sia dall'evoluzione del concetto di spazio in fisica.
1 Si ricordi infatti che in logica classica una proposizione falsa implica qualsiasi proposizione.
2. La geometrìa euclidea
In questo paragrafo analizziamo una assiomatica euclidea, che è un sistema di postulati e di termini primitivi a partire dai
quali si può costruire quella che per tanto tempo è stata semplicemente la Geometria e che oggi chiamiamo geometria euclidea.
Per questo scopo non possiamo servirci delle formulazioni originali di Euclide, che ormai hanno soltanto un interesse storico.
Il sistema che presentiamo è simile a quello proposto da Hilbert3 negli ultimi anni dell'800: esso consiste in un elenco di termini
primitivi e in cinque gruppi di assiomi.
Termini primitivi:
punto, retta, piano, tra, appartenere,4 movimento.
Gruppo I: assiomi di appartenza
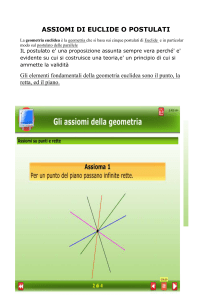
I.1. Due punti distinti qualsiasi appartengono a una e una sola retta.
I.2. A ogni retta appartengono almeno due punti; a ogni piano appartengono almeno tre punti.
I..3. Tre punti che non appartengono a una stessa retta appartengono a uno e un solo piano.
I..4. Se due punti di una retta appartengono a un piano, allora tutti i punti di quella retta appartengono a quel piano.
Osservazioni:
Si noti che l'assioma 1.1 implica che due rette non possono avere più di due punti comuni senza coincidere, ma non implica che abbiano
sempre almeno un punto in comune. Si ammette dunque l'esistenza di rette prive di punti comuni, che invece è esclusa nella geometria proiettiva.
Per comodità si usano espressioni che, sebbene non esplicitamente definite, non sono da aggiungere all'elenco dei termini primitivi, perché
traggono il loro significato dagli assiomi che via via vengono enunciati. Per esempio possiamo usare l'espressione "la retta passante per due punti
dati", perché l'esistenza di una retta alla quale appartengono due punti dati è assicurata dal I gruppo di assiomi.
Gruppo II: assiomi dell'ordine
II.1. Se A, B e C sono tre punti allineati e B giace tra A e C, allora B giace tra C e A.
II.2. Dati due punti A e B su una retta, si può sempre trovare un terzo punto della retta che giace tra A e B.
II.3. Dati tre punti su una retta, uno soltanto di essi giace tra gli altri due.
II.4. Se una retta incontra un lato di un triangolo in un punto che non è un vertice, allora incontra anche un altro lato.
Osservazioni:
Gli assiomi dell'ordine definiscono (implicitamente) il termine primitivo “tra” e stabiliscono su una retta due ordinamenti opposti.
Consentono inoltre di definire un segmento come l'insieme dei punti che giacciono tra due punti dati; si possono dunque definire lato e triangolo,
il che rende comprensibile l'assioma 2.4.
Si noti anche che l'assioma 2.2 implica che a una retta appartengono infiniti punti e stabilisce che una retta ha la proprietà di essere densa.
Negli Elementi Euclide ammette alcune ipotesi, senza dimostrarle né includerle tra i postulati. Una di queste ipotesi è la seguente: "una
retta r divide il piano in due regioni, aventi le proprietà: 1) un punto di una regione e un punto dell'altra sono gli estremi di un segmento che
incontra r; 2) due punti di una stessa regione sono gli estremi di un segmento che non incontra r". Nei Fondamenti di Hilbert questo enunciato è un
teorema che viene dimostrato per mezzo degli assiomi dei primi due gruppi.
Gruppo III: assioma delle parallele
III.l. Dati una retta e un punto che non le appartiene, esiste una e una sola retta passante per quel punto e parallela alla retta
data.
Gruppo IV: assiomi dei movimenti
IV.1. I movimenti sono trasformazioni del piano che formano un gruppo.
IV.2. I movimenti trasformano segmenti in segmenti (e quindi rette in rette).
IV.3. Data una semiretta s di origine O, sia uno dei due semipiani in cui il piano è diviso dalla retta di s; si prendano poi, con
analogo significato, s', O' e '. Allora esiste un movimento, e uno solo, che trasforma s in s', O in O' e in '.
Osservazione
Gli assiomi del gruppo IV definiscono il termine primitivo movimento. I movimenti così definiti sono trasformazioni piane che mutano
rette in rette e dunque sono affinità. Se poi aggiungiamo che per definizione due segmenti hanno la stessa lunghezza se esiste un movimento che
porta l'uno sull'altro, si ottiene la geometria delle isometrie, detta geometria metrica. Si noti che in questo modo si introduce anche la nozione di
congruenza come sovrapponibilità per mezzo di un movimento o, meglio, uguaglianza a meno di un movimento. Si potranno poi dedurre le
proprietà formali della congruenza come relazione riflessiva, simmetrica e transitiva. Si potrebbe seguire la strada inversa, come fece lo stesso
Hilbert: definire prima il termine primitivo congruenza con appropriati assiomi e poi i concetti di trasformazione piana e di isometria. Allora nel
gruppo IV si enuncerebbero i seguenti due assiomi: 1) la congruenza è una relazione di equivalenza; 2) due triangoli che hanno due lati e l'angolo
tra questi compreso congruenti, hanno congruenti anche gli altri due angoli.
2 B. Russel scrisse ironicamente che la matematica è la scienza nella quale non si sa di cosa si parla.
3 L'opera di David Hilbert cui ci riferiamo è Grundlagen der Geometrie (Fondamenti della Geometria).
4 II termine appartenere può essere escluso dall'elenco, in quanto proveniente dalla teoria degli insiemi; a condizione, naturalmente, che quest'ultima sia supposta nota.
In tal modo il I criterio di congruenza dei triangoli è assunto come postulato. Se invece si assumono come postulati le proposizioni relative ai
movimenti, esso diviene un teorema, la cui dimostrazione, come si ricorderà dai corsi del biennio, implica movimenti e sovrapposizioni. La scelta
tra un gruppo di assiomi che definisca la congruenza e un gruppo che definisca i movimenti dipende dalla volontà di sottolineare l'importanza,
rispettivamente, del concetto intuitivo di uguaglianza oppure del concetto di invarianza delle proprietà geometriche rispetto a gruppi di
trasformazioni. La seconda opzione è spesso preferita dai matematici moderni (e dai libri di testo), perché mette in luce il senso più profondo
della geometria.
Osserviamo anche che l'assioma IV.3, la cui relazione con gli altri non è immediatamente percepibile, è formulato in modo che tra i movimenti
siano compresi i ribaltamenti.
Gruppo IV: assioma di continuità
V.l. Ogni partizione di una retta in due classi disgiunte, tale che tutti i punti della prima classe precedano tutti i punti della
seconda, ammette sulla stessa retta uno e un solo punto di separazione, tale cioè che ogni punto della retta che lo precede appartiene
alla prima classe e ogni punto che lo segue alla seconda.
Osservazione:
Questo assioma, detto assioma di continuità o di Dedekind, in breve afferma che per ogni sezione di una retta in due classi, c'è un punto
che è l'ultimo della prima classe o il primo della seconda. È evidente che l'assioma di Dedekind enuncia una proprietà dell'ordinamento della retta.
Si può dimostrare che se si accetta l'assioma delle parallele, l'assioma di continuità può essere sostituito dai due seguenti:
1) Assioma di Archimede. Dati due punti A e B su una retta, supposto che A preceda B, si può costruire a partire da A una successione di
segmenti AA1, AA2, A2A3, ecc., tutti congruenti tra loro, fino a trovare un punto che segue B.
2) Assioma di completezza. Se E è un sistema di punti e rette del piano che soddisfa tutti gli assiomi precedentemente enunciati (compreso
quello di Archimede), non è possibile aggiungere a E altri elementi (altri "punti" e altre "rette"), in modo che il sistema ampliato soddisfi gli
stessi assiomi.
Nella geometria iperbolica e nella geometria ellittica, dove non vale l'assioma delle parallele, il postulato di continuità non è equivalente ad
"Archimede + completezza" e deve perciò essere mantenuto.
3. Il problema della compatibilità
Gli assiomi della geometria euclidea sono compatibili? Hilbert dimostrò che l'assioma di continuità permette di stabilire
una corrispondenza biunivoca tra i punti di una retta e i numeri reali. Egli partì da qui per proporre un modello algebrico della
geometria euclidea. In questo modello "punto" è una coppia ordinata di numeri reali (x, y) e "retta" un'equazione di primo grado
(lineare) in x e y: ax + by + c = 0. Tutti i concetti della geometria hanno nel modello un'appropriata definizione. Per esempio un
punto "appartiene a una retta" se le sue coordinate soddisfano l'equazione della retta e pertanto due rette sono "parallele" se il
sistema algebrico formato con le loro equazioni non ammette nessuna soluzione. Anche concetti più complessi sono definiti nel
modello di Hilbert per via algebrica. Per esempio una isometria può essere definita come una trasformazione i tale che:
i ( x, y ) = ϕ ( x, y ) + ( λ , µ )
dove (λ , µ ) è un dato "punto" e ϕ è una trasformazione lineare la cui matrice è
a −c
a c
oppure
con a 2 + c 2 = 1 .
c a
c −a
I "punti" e le "rette" di questo modello soddisfano tutti gli assiomi della geometria euclidea. In tal modo la questione della
compatibilita degli assiomi della geometria è ricondotta a quella della compatibilita del sistema dei numeri reali, che a sua
volta è un sistema assiomatico; dunque il problema è solo spostato. Si può soltanto dire che se capitasse di dimostrare due tesi
contradditorie in geometria o nell'algebra dei numeri reali, si dovrebbe concludere che entrambi i sistemi sono contradditori.
Osservazione
Un importante risultato della logica del XX secolo asserisce peraltro che la compatibilita di un sistema di postulati non può essere stabilita
all' interno dello stesso sistema. Più precisamente: se gli assiomi sono in contraddizione tra loro, allora qualunque teorema può essere
dimostrato insieme con il suo contrario, dunque sia la compatibilita, sia la non compatibilita possono essere dimostrate. Ma se gli assiomi
sono compatibili, la loro compatibilità non può essere da essi dedotta come teorema. Questo risultato è noto come teorema di Gödel.
Un celebre tentativo di fondare la matematica sulla logica è contenuto nei Principia Mathematica di Russel e Whitehead. Nei Principia tutta la
matematica è costruita a partire dalla teoria degli insiemi. In quest'ultima le proposizioni e i termini primitivi hanno un significato concreto: non
sono cioè suscettibili di diverse interpretazioni. Perciò la teoria degli insiemi non sarebbe un vero e proprio sistema assiomatico e la questione
della compatibilità non si porrebbe nel modo cui abbiamo accennato.
4. Il postulato delle parallele
Per ciò che riguarda l'indipendenza degli assiomi, storicamente le maggiori attenzioni sono state riservate al postulato
delle parallele (il nostro assioma III.l). È stato notato che negli Elementi lo stesso Euclide sembra guardarlo con sospetto; egli
infatti preferì dimostrare alcuni teoremi seguendo vie complicate, sebbene il ricorso all'assioma delle parallele potesse
consentire dimostrazioni più semplici.
Euclide introdusse l'assioma soltanto quando lo ritenne inevitabile.5 La singolarità di questo postulato consiste nel fatto che
esso non sembra avere quelle caratteristiche di evidenza sperimentale che venivano riconosciute agli altri postulati. Si
consideri infatti la figura 16.1; vi sono molte rette uscenti da P che hanno la proprietà di non intersecare la retta r entro una
distanza finita, ma non è affatto evidente che una di esse possieda quella proprietà all'infinito: nessun modello concreto, fatto
di fili o altro (necessariamente di lunghezza finita), ne potrà dare una verifica sperimentale. Gli altri assiomi enunciano invece
proprietà riguardanti estensioni limitate e dunque suscettibili di verifiche sperimentali per mezzo di modelli materiali.
r
La non verifìcabilità empirica non è un argomento logico contro un postulato, ma è abbastanza per giustificare i
numerosi tentativi di dimostrare l'assioma delle parallele, che sono stati intrapresi per molti secoli. La questione era di
provare che l'assioma non è indipendente dagli altri. Tra i molti tentativi,6 per noi è interessante ricordare soprattutto quello
del gesuita Saccheri,7 che si distingue per la tecnica di dimostrazione indiretta: Saccheri ammise il contrario dell'assioma delle
parallele e giunse a conclusioni che egli giudicò assurde; ritenne pertanto di aver dimostrato per assurdo l'assioma delle
parallele. Tali conclusioni, come sappiamo oggi, sono in realtà teoremi validi nelle geometrie non euclidee. Ma l'opinione
dominante al tempo di Saccheri era che la geometria euclidea avesse una validità assoluta e ciò impedì al bravo gesuita di
diventare lo scopritore delle geometrie non euclidee.
Nel corso del XIX secolo la ricerca prese una via completamente diversa: Lobatchewskj e Bolyai costruirono una nuova
geometria, utilizzando tutti gli assiomi della geometria euclidea tranne il postulato delle parallele. Essi dimostrarono un
certo numero di teoremi e provarono così che una geometria senza quel postulato è logicamente del tutto plausibile. Ma
plausibile non significa compatìbile; vedremo ora quale fu l'ulteriore passo in avanti, che consentì di porre l'intera
questione della compatibilita e della indipendenza degli assiomi in termini attuali.8
5. La geometrìa iperbolica
Nel paragrafo 3 abbiamo accennato al modello algebrico di Hilbert per la geometria euclidea. In quel modello tutti
gli assiomi, compreso quello delle parallele, sono verificati; questa dimostrazione è alla portata di chiunque possieda qualche
conoscenza di geometria analitica. Ora illustreremo il modello di Klein, che è invece un modello per una geometria in cui il
postulato delle parallele non è valido.
Nella rappresentazione visiva della geometria euclidea il punto, la retta e il piano sono astrazioni idealizzate di realtà
concrete: una macchia d'inchiostro molto piccola, un raggio luminoso prolungato all'infinito, l'estensione indefinita della
piatta superficie di un lago. Tutti questi oggetti sono contenuti nello spazio fisico ordinario, l'universo della nostra
esperienza sensoriale. Nel modello di Klein l'"universo" è molto differente. Immaginiamo che il mondo sia fatto come un
cerchio; possiamo muoverci all'interno del cerchio in due sole dimensioni, come se ci trovassimo in un'immensa distesa piatta,
circondati da un orizzonte circolare. Al di là della circonferenza-limite non c'è nulla e la circonferenza stessa è inaccessibile.
Ora definiamo gli enti fondamentali del modello di Klein, che scriveremo in caratteri CORSIVI MAIUSCOLI; con caratteri
normali indicheremo i punti, le rette e il piano euclidei.
PUNTO: ogni punto interno alla circonferenza
RETTA: ogni corda (estremi esclusi)
PIANO: l'insieme dei PUNTI
I punti della circonferenza-limite e la circonferenza stessa si possono considerare gli elementi all'infinito o impropri del
PIANO.
5 L'enunciato euclideo del postulato delle parallele (V postulato negli Elementi) è il seguente: "Se due rette formano con una retta due angoli da una stessa parte e la somma dei due angoli
è minore di due angoli ret-ti, allora le due rette si incontrano dalla stessa parte dei due angoli."
6 Alcuni di essi già in epoca antica, per esempio Proclo nel IV sec. a. C.
7 Saccheri (1667-1733) scrisse Eudìdes ab omni naevo vindicatus.
8 II russo Nikolaj I. Lobatchewskj (1793-1856) nei Nuovi Prìncipi della Geometrìa (1835) e l'ungherese Janos Bolyai (1802-1860) nell'appendice a un altro lavoro (1832)
giunsero per vie indipendenti e quasi contemporaneamente ai loro risultati. Altri matematici contemporanei lavorarono alla questione dell'indipendenza del postulato delle
parallele. Tra essi Riemann, di cui parleremo, e prima ancora Gauss, il più grande matematico del tempo. Gauss evitò di pubblicare le sue ricerche perché temeva, come egli
scrisse, "le grida degli sciocchi".
È facile vedere che gli assiomi dell'appartenenza sono validi in questo modello. Per esempio (fig.1) per due PUNTI passa una e
una sola RETTA. Inoltre su ogni RETTA si può introdurre in modo "naturale" un ordinamento che soddisfa gli assiomi
dell'ordine e della continuità.
L'assioma delle parallele è l'unico non valido. Prendiamo (fig.2) infatti una RETTA r e un PUNTO P che non le appartiene:
allora infinite RETTE passanti per P non incontrano r. Due di queste incontrano r all'infinito e potranno essere definite come le
PARALLELE a r per P.
fig.1
fig.2
Nella geometria descritta dal modello di Klein vale perciò l'assioma: "per un punto esterno a una retta passano due
parallele alla retta data". Con ciò è dimostrata l'indipendenza dell'assioma delle parallele dagli altri della geometria euclidea; se
infatti quell'enunciato fosse dimostrabile, esso sarebbe un teorema valido anche nel modello di Klein, il che, come si è visto, non
avviene.
Esistono "movimenti" che nel modello di Klein soddisfano gli assiomi euclidei del gruppo IV? Tali movimenti devono
trasformare RETTE in RETTE, cioè corde in corde; devono dunque conservare gli allineamenti e trasformare in sé la
circonferenza-limite (e quindi portare punti interni in punti interni). Le più generali trasformazioni piane che mutano rette
in rette sono le proiettività. Si può dimostrare che esistono infinite proiettività che trasformano una circonferenza in sé e tali
proiettività formano un gruppo. Questi "movimenti iperbolici" soddisfano anche l'assioma IV.3, purché si dia ai termini che vi
compaiono il giusto significato: una SEMIRETTA uscente da un PUNTO sarà un tratto di corda da quel punto alla
circonferenza e un SEMIPIANO sarà una delle due regioni in cui il cerchio è diviso da una corda.
Nel modello di Klein ogni concetto trova un'adeguata interpretazione dunque esso costituisce un modello della geometria di
Lobatchewskj-Bolyai o geometria iperbolica, i cui assiomi sono esattamente quelli della geometria euclidea, con l'eccezione
dell'assioma delle parallele: nella geometria iperbolica da un punto si possono condurre due parallele a una retta, anziché
una sola. Tale geometria è non contradditoria? Il modello di Klein soddisfa gli assiomi euclidei, tranne uno, dunque sarebbe
contradditorio soltanto se lo fosse anche la geometria euclidea. Ne segue che la geometria iperbolica e quella euclidea sono
logicamente altrettanto accettabili.
6 La geometria ellittica
Esisteranno altre geometrie altrettanto legittime della geometria di Euclide e di quella di Lobatchewskj-Bolyai. Un
semplice modello della geometria ellittica, o geometria di Riemann,9 nella quale non esistono rette parallele.
Immaginiamo che il nostro universo sia la superficie a due dimensioni di una sfera. Non c'è nulla né sopra né sotto la
superficie e il nostro problema sarebbe di costruire una geometria adatta a descrivere un mondo siffatto. In tali condizioni una
soluzione ragionevole sarebbe quella di definire le "linee rette" come le linee di minima distanza o linee geodetiche, che su
una superficie sferica sono i circoli massimi. Definiamo allora nel modo seguente i termini primitivi della geometria di
Riemann:
PUNTO: un punto della superficie sferica
RETTA: un circolo massimo
PIANO: l'insieme dei PUNTI (la superficie sferica)
Per un abitante dell'universo di Riemann, un arco di circolo massimo sarebbe dunque un SEGMENTO: la via più breve
per unire due punti, proprio come sul piano euclideo. Accanto a questa analogia, vi sono però differenze importanti; prima fra tutte
la seguente: due RETTE si incontrano sempre in due PUNTI (fig.3), perciò non esistono rette parallele. Nella geometria di Riemann
l'assioma delle parallele non è valido e dovrebbe essere sostituito dall'enunciato: "per un PUNTO esterno non si può condurre
nessuna parallela a una RETTA data".
fig.3
fig.4
Inoltre può accadere che per due PUNTI passino infinite RETTE; è il caso degli estremi di un diametro della sfera (fig.4):
tutti i meridiani terrestri passano per i poli. Pertanto il primo assioma di appartenenza viene sostituito con il seguente: "per due
PUNTI passa sempre almeno una RETTA (ma non sempre una sola)".
Il fatto che nell'universo sferico le RETTE siano linee chiuse di lunghezza finita renderà poi necessario ridefinire il termine
primitivo tra, perciò anche gli assiomi dell'ordine dovranno essere modificati.
fig.5
Con opportune definizioni dei concetti, si deduce dai nuovi postulati una geometria differente da quella euclidea. Un
risultato caratteristico è, per esempio, il seguente: tutte le RETTE PERPENDICOLARI a una RETTA data hanno due PUNTI
in comune (fig.5); i meridiani terrestri sono PERPENDICOLARI all'equatore e passano per i poli.
Questa nuova geometria è non-contradditoria nella stessa misura in cui lo è quella euclidea. Infatti tra i PUNTI e le
RETTE di un PIANO di Riemann ci sono le stesse relazioni che sussistono fra i punti e i circoli massimi di una superficie
sferica euclidea; in altri termini il modello sferico è un'interpretazione della geometria di Riemann per mezzo di oggetti
euclidei: ogni teorema della geometria di Riemann non è altro che un teorema euclideo, enunciato con parole differenti.
7. Quale geometrìa è quella vera?
È possibile considerare da un punto di vista unitario la geometria di Euclide, quella di Riemann e quella di LobatchewskjBolyai. Immaginiamo che l'universo sia una superficie curva qualsiasi, non necessariamente sferica, e definiamo rette le linee
geodetiche della superficie. Un cammino rettilineo tra due punti è cioè per definizione il cammino più breve tra quei punti.
Un punto di una tale superficie può essere di due tipi: punto ellittico, se si trova, per così dire, come sulla sommità di una
collinetta; punto iperbolico, se si trova come in fondo a una buca. La porzione di superficie vicina a un punto ellittico è simile a
una superficie sferica e su di essa le proprietà geometriche sono quelle della geometria di Riemann, che per questo motivo si
dice ellittica; vicino a un punto iperbolico, la geometria valida è quella di Lobatchewskj-Bolyai, che infatti è detta iperbolica.
La geometria di una tale superficie può dunque variare localmente. Ora, come può un osservatore stabilire quale geometria
costituisce la migliore approssimazione per descrivere la porzione di spazio fisico dove egli si trova? Egli potrebbe ripetere, per
esempio, l'esperimento di Gauss, il quale tentò, con un metodo topografico, di verificare se la somma degli angoli interni di un
triangolo reale misurasse 180°. Questo è un punto cruciale, perché il teorema euclideo "la somma degli angoli interni di un
triangolo è uguale a un angolo piatto" è equivalente all'assioma delle parallele. Il risultato fu effettivamente circa 180°, ma
poiché l'errore poteva essere compreso nell'incertezza strumentale, l'esperimento non potè dare un risultato conclusivo.10
Non c'è dubbio che la nostra intuizione, per così dire, è euclidea, nel senso che la geometria euclidea sembra "quella giusta"
all'esperienza comune. Ciò può forse essere spiegato con il fatto che l'esperienza quotidiana concerne piccole porzioni dello
spazio fisico e la curvatura ellittica o iperbolica di un'estensione di superficie molto piccola non si può distinguere da quella
di un piano. In altre parole, se quella superficie è così piccola da poter essere considerata piana, la geometria valida è con
buona approssimazione quella di Euclide, che in un certo senso è un caso limite sia della geometria ellittica, sia di quella
iperbolica.
Osservazione In questo vi è un'analogia con il fatto che la fisica relativistica usa la geometria di Riemann per descrivere i fenomeni cosmici. Lo
spazio fisico avrebbe una curvatura variabile, determinata dalla concentrazione locale di materia. I raggi luminosi seguono le geodetiche dello
spazio, che però, per piccole estensioni di questo, sono rette euclidee. Perciò è del tutto ragionevole che in laboratorio, che è appunto una piccola
estensione dello spazio fisico, si usi la geometria di Euclide negli esperimenti sul cammino rettilineo dei raggi luminosi.
La questione di quale sia la geometria "vera", cioè più adatta per descrivere l'universo reale, riguarda i risultati di osservazioni
sperimentali ed è perciò un problema fisico, non matematico. In questo senso la geometria ridiventa, per così dire, un ramo della
fisica, secondo l'etimologia stessa della parola (misura della terra). In questo paragrafo abbiamo dunque in parte deviato
dalle linee di un'esposizione puramente matematica. Nella geometria come ramo della matematica, contano soltanto le
connessioni logiche tra i postulati: ogni geometria fondata su un sistema di assiomi compatibili è, in matematica, logicamente
accettabile.
La geometria che si studia a scuola è euclidea. In particolare la metrica euclidea è quella del gruppo delle isometrie, nella
9. Bernhard Riemann (1826-1866) fu uno dei più brillanti matematici deU'800.
10. Se lo scostamento da 180° del valore misurato da Gauss fosse stato sensibilmente maggiore dell'incertezza strumentale, si sarebbe potuto concludere che la geometria
euclidea non è valida. Un tale esperimento non può in nessun caso stabilire che la geometria euclidea o un'altra geometria, è valida. Nella geometria euclidea la somma degli
angoli interni di un triangolo è 180°, nella geometria ellittica è maggiore di 180°, nella geometria iperbolica è minore di 180°.
quale due figure si considerano uguali (a meno di un'isometria) se sono traslate o ruotate o ribaltate l'una rispetto all'altra.
Perciò si può dire che nella geometria metrica né un semplice cambiamento di posizione o di direzione né un
ribaltamento11 mutano una figura in modo essenziale. Perciò nella geometria metrica le posizioni e le direzioni sono
indifferenti, nel senso che non ha importanza quale posizione una figura occupa rispetto a un punto prefissato né di quale
angolo sia ruotata rispetto a una direzione prefissata. La metrica euclidea descrive le proprietà dello spazio fisico omogeneo e
isotropo12 della fisica classica, nella quale non esistono in natura posizioni né direzioni privilegiate e dunque neppure un sistema
di riferimento assoluto, rispetto al quale descrivere traiettoria, velocità e accelerazione di un punto materiale; si può scegliere
qualunque punto come origine del riferimento e gli assi del sistema in qualunque direzione.
Sempre nell'ambito euclideo, una generalizzazione della geometria metrica è la geometria simile, le cui trasformazioni
fondamentali formano il gruppo delle similitudini. Quindi i "movimenti" della geometria simile sono le similitudini e pertanto la
nozione di uguaglianza va interpretata diversamente. Tutti gli invarianti della geometria metrica sono tali anche nella
geometria simile, tranne le lunghezze dei segmenti; però i rapporti tra le lunghezze sono invarianti per similitudini, perciò
praticamente tutte le proprietà non metriche delle figure sono invarianti. Per esempio un poligono simile a un triangolo sarà
un triangolo, un triangolo simile a un triangolo isoscele sarà isoscele e così via. La geometria simile è la geometria che si
impara nei corsi elementari. Quando l'insegnante dimostra alla lavagna una proprietà di una figura, lo studente può seguire la
dimostrazione riproducendo sul suo foglio una figura simile a quella disegnata dall'insegnante; per le due figure quella
proprietà sarà ugualmente valida.
Una generalizzazione più importante è il gruppo delle affinità, che sono le trasformazioni fondamentali (i "movimenti")
della geometria affine. Le affinità sono le più generali corrispondenze biunivoche tra punti del piano euclideo che
trasformano rette in rette (e quindi rette parallele in rette parallele). Le figure cambiano forma, entro certi limiti, determinati
dall'invarianza del parallelismo; la figura affine di un parallelogramma è un parallelogramma, ma le ampiezze degli angoli e i
rapporti tra i lati possono cambiare, perciò la figura affine di un rettangolo sarà un parallelogramma, ma in generale non sarà un
rettangolo. Di conseguenza a rette perpendicolari in generale non corrispondono rette perpendicolari e pertanto la nozione di
perpendicolarità non è ammessa nella geometria affine. Continuano peraltro a valere gli assiomi della geometria euclidea,
compreso quello delle parallele.
In sintesi
Il metodo per la costruzione delle teorie matematiche è assiomatico. Un ristretto numero di assiomi (postulati) definisce in modo implicito
i termini primitivi della teoria; tutti gli enunciati successivamente asseriti sono dimostrati a partire dagli assiomi, attraverso l'applicazione
delle j| regole del ragionamento logico. Gli assiomi non sono dimostrati e nemmeno è necessario darne ;ij una qualsiasi giustificazione.
L'essenziale è che siano compatibili, cioè non-contradditori. È an- 1 che richiesto, per ragioni di economia, che siano indipendenti,
sebbene ciò non sia strettamente necessario per la validità della teoria.
Gli assiomi della geometria metrica euclidea sono quelli di appartenenza, dell'ordine, di continuità e dei movimenti (isometrie), più l'assioma
delle parallele. Il modello di Hilbert per la geometria euclidea è di tipo algebrico. In tale modello un "punto" è una coppia di numeri, una
"ret- ,j ta" l'insieme dei "punti" che soddisfano un'equazione lineare e così via. Ogni concetto euclideo ha un equivalente analitico. Tale
modello non risolve la questione della compatibilita degli assiomi euclidei: infatti questi ultimi saranno non-contradditori se tali saranno
quelli della teoria dei numeri reali e viceversa.
Nella comune interpretazione empirica dei concetti primitivi euclidei (punto, retta e piano), gli assiomi hanno una "evidenza"
sperimentale tale che la geometria euclidea è stata a lungo ritenuta l'unica possibile, in quanto fedele rappresentazione delle proprietà dello
spazio fisico. Faceva eccezione l'assioma delle parallele, che sembrava "poco evidente" e perciò era ritenuto non indipendente dagli altri.
In realtà l'assioma delle parallele non può essere dimostrato. È infatti possibile costruire una geometria, detta geometria iperbolica, nella
quale tutti gli assiomi euclidei, tranne quello delle parallele, sono validi. Un modello di geometria iperbolica è il modello di Klein, nel quale
i concetti primitivi e quelli derivati devono essere interpretati in modo diverso dal caso euclideo. La geometria iperbolica è logicamente
altrettanto valida della geometria euclidea. Di grande importanza è la geometria ellittica. Un modello per la geometria ellittica è quello della
superficie sferica, dove le "rette" sono i circoli massimi. Nella geometria ellittica non ci sono rette parallele e gli assiomi euclidei
dell'appartenenza e dell'ordine non sono validi.
11 Si ha un ribaltamento quando l'isometria contiene un numero dispari di simmetrie assiali .
12 Omogeneo: lo spazio ha le stesse proprietà in ogni luogo. Isotropo: lo spazio ha le stesse proprietà in ogni direzione.