yzaaaa P (a,a) C

PROBLEMA 10
4 FILI LUNGHI CONDUTTORI SONO TRA LORO PARALLELI E DISPOSTI AI VERTICI DI
UN QUADRATO DI LATO a = 20 cm; IN OGNI FILO CIRCOLA LA CORRENTE i = 30 A,
CON I VERSI MOSTRATI IN FIGURA.
A) CALCOLARE IL CAMPO MAGNETICO BC NEL CENTRO C DEL QUADRATO.
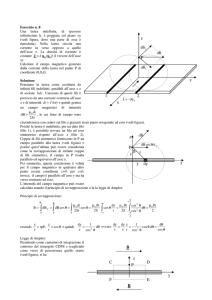
La figura che segue mostra la disposizione dei 4 fili conduttori:
z
3
.
4
a
. C
a
1
P (a,a)
a
.
a
2
y
I fili giacciono lungo l’asse x (l’asse perpendicolare al piano del foglio) e sono stati indicizzati con i numeri da
1 a 4; nei fili 1 e 3 la corrente ha verso uscente dal foglio (ovvero nel verso positivo delle x), nei fili 2 e 4 ha
verso entrante nel foglio (ovvero nel verso negativo delle x).
E’ noto dalla teoria che un filo conduttore di lunghezza infinita in cui circola una corrente i, produce in un
punto P distante r un campo magnetico ⃗ pari a :
⃗
̂
(1)
dove ̂ è il versore individuato dalla regola della mano destra, come mostrato in figura:
r
⃗
𝐵
i
In definitiva, il campo magnetico generato da un filo in un punto dello spazio distante r dal filo stesso ha la
direzione ortogonale alla direzione di r, giace nel piano ortogonale al filo e contenente r, e il verso definito
dalla regola della mano destra.
Nel nostro caso, utilizzando il principio di sovrapposizione, consideriamo il campo magnetico prodotto da
ciascun filo nel punto C e poi sommiamo gli effetti. Il risultato che si ottiene è mostrato in figura (il pedice
di ⃗⃗⃗ richiama l’indice del filo i corrispondente):
z
3
.
1
⃗⃗⃗⃗
𝐵1
.
4
⃗⃗⃗⃗
𝐵
⃗⃗⃗⃗
𝐵4
a
P (a,a)
a
.
C
a
⃗⃗⃗⃗
𝐵3
a
2
y
Notiamo che i 4 fili hanno tutti la stessa distanza dal punto C, centro del quadrato, che è pari a metà
diagonale del quadrato, ovvero
√
. Quindi i ⃗⃗⃗ avranno tutti lo stesso modulo:
|⃗⃗⃗⃗1 |
|⃗⃗⃗⃗ |
|⃗⃗⃗⃗3 |
|⃗⃗⃗⃗4 |
√
Per sommare i 4 contributi conviene introdurre un sistema di riferimento cartesiano centrato nel punto C e
con gli assi paralleli agli assi y e z. Per ovvie ragioni di simmetria i 4 vettori ⃗⃗⃗ formeranno con l’asse y (e
quindi anche con l’asse z) un angolo di 45°.
Lungo l’asse y si avrà:
(|⃗⃗⃗⃗ |
|⃗⃗⃗⃗3 |
|⃗⃗⃗⃗1 |
|⃗⃗⃗⃗4 |
)̂
Poiché i moduli sono uguali tra loro, il risultato è il vettore nullo. Il campo magnetico risultante non ha
componente lungo l’asse delle y.
Lungo l’asse z si avrà:
(|⃗⃗⃗⃗ |
|⃗⃗⃗⃗3 |
|⃗⃗⃗⃗1 |
|⃗⃗⃗⃗4 |
)̂
√
̂
Il campo magnetico risultante ⃗⃗⃗⃗ nel punto C giace completamente lungo l’asse z ed ha espressione:
⃗⃗⃗⃗
√
√
̂
̂
(
4)
̂
B) CALCOLARE IL CAMPO MAGNETICO BP NEL VERTICE P DEL QUADRATO.
Per calcolare il campo magnetico nel punto P di coordinate (a,a) utilizziamo ancora il principio di
sovrapposizione, come nel caso precedente: valutiamo i contributi dati singolarmente dai fili 1, 2 e 3 nel
punto P e poi li sommiamo. In figura è mostrato il risultato che si ottiene:
z
3
⃗⃗⃗⃗
𝐵3
⃗⃗⃗⃗
𝐵1
.
⃗⃗⃗⃗
𝐵
a
4 P (a,a)
a
a
.
C
1
.
a
2
y
Utilizzando la (1), possiamo valutare immediatamente i moduli dei singoli contributi ⃗⃗⃗ :
|⃗⃗⃗⃗1 |
√
|⃗⃗⃗⃗ |
|⃗⃗⃗⃗3 |
Per sommare i 3 singoli contributi conviene introdurre un sistema di riferimento cartesiano centrato nel
punto P e con gli assi paralleli agli assi y e z. Per ovvie ragioni di simmetria il vettore ⃗⃗⃗⃗1 forma con l’asse y (e
quindi anche con l’asse z) un angolo di 45°.
Lungo l’asse y si avrà:
(|⃗⃗⃗⃗ |
|⃗⃗⃗⃗1 |
)̂
Usando le espressioni appena scritte per |⃗⃗⃗⃗1 | e |⃗⃗⃗⃗ |, si ha:
(
√
√
)̂
(
)̂
Lungo l’asse z si avrà:
(|⃗⃗⃗⃗3 |
Usando le espressioni per |⃗⃗⃗⃗1 | e |⃗⃗⃗⃗3 |, si ha:
|⃗⃗⃗⃗1 |
)̂
̂
√
(
√
)̂
(
)̂
̂
In definitiva il campo magnetico ⃗⃗⃗⃗ nel punto P avrà la seguente espressione:
⃗⃗⃗⃗
4
̂
3
4
̂
5)
(
̂
5)
(
̂
(2)
C) LA FORZA PER UNITA’ DI LUNGHEZZA SUL FILO DISPOSTO IN P.
E’ noto dalla teoria che un filo lungo l percorso da una corrente i e immerso in un campo magnetico ⃗
risente di una forza la cui espressione è data da:
⃗
dove è un vettore con modulo pari a i, e verso e direzioni definiti dalla corrente i.
La forza per unità di lunghezza ⃗⃗⃗ sarà:
⃗⃗⃗
⃗
Nel nostro caso abbiamo un filo percorso da corrente nel punto P e immerso in un campo magnetico ⃗⃗⃗⃗
precedentemente stimato nella (2). In base al risultato appena scritto, la forza per unità di lunghezza ⃗⃗⃗ sarà
pari a:
⃗⃗⃗
⃗⃗⃗⃗
̂
dove il segno meno discende da fatto che la corrente ha il verso discorde rispetto all’asse x.
Sostituendo la (2) si ottiene:
⃗⃗⃗
⃗⃗⃗⃗
̂
̂
(
̂
̂)
(̂
(̂
̂)
̂)
Dalle nozioni elementari sul prodotto vettoriale tra versori di un sistema di riferimento cartesiano 3D è
noto che:
̂
(̂
̂
̂)
̂
̂
e quindi:
⃗⃗⃗
̂
̂
(
3)
̂
(
4)
̂