Nota sull’Analisi .....(2a ed.)
9
Confronto fra due o più
popolazioni attraverso test non
parametrici
I test non parametrici prescindono per la loro validità dalle condizioni di normalità ed
omogeneità delle varianze delle popolazioni statistiche considerate. In effetti, appartengono a
questa categoria anche i test esaminati nel corso del capitolo 2. Qui, con riferimento alla
presenza di una variabile di risposta continua, ci limitiamo a considerare quei test adatti
all'analisi di esperimenti comprendenti un solo fattore fisso.
I test non parametrici direttamente contemplati da una PROC statistica in SAS sono quelli
relativi a campioni indipendenti; restano perciò esclusi i test per campioni associati a coppie
(test dei segni; test dei ranghi delle differenze di Wilcoxon).
Nell'ambito dei test disponibili, si possono distinguere due classi di test non parametrici in
funzione della modalità di trasformazione della variabile di risposta . Nei test delle mediane si
calcola il valore della mediana per l'insieme delle unità sperimentali della prova, per poi
calcolare per ciascun trattamento la proporzione di unità sperimentali al di sopra ed al di sotto
di tale valore e confrontare tali proporzioni con un test χ2. Nei test dei ranghi i valori numerici
originali dell'insieme delle unità sperimentali sono sostituiti con i loro ranghi, cioè con la loro
posizione in graduatoria, per poi confrontare la somma dei ranghi dei trattamenti con dei valori
teorici attesi per l'ipotesi nulla di campioni appartenenti alla stessa popolazione statistica.
I test dei ranghi comportano una perdita di precisione, rispetto al test t ed alla analisi della
varianza nelle loro condizioni di applicazione, dell'ordine del 5 % ; per i test delle mediane tale
perdita è sensibilmente maggiore, intorno al 30 % nella maggior parte dei casi. L'uso di questi
test è comunque molto limitato nella sperimentazione agronomica, essendo raccomandato nel
solo caso in cui nè la variabile di risposta originale nè alcuna trasformazione della stessa
consenta di rientrare nelle condizioni per l'applicazione dei test parametrici. Per applicare
questi test, la sola condizione richiesta è invece quella di campioni casuali e, nei casi in esame,
indipendenti.
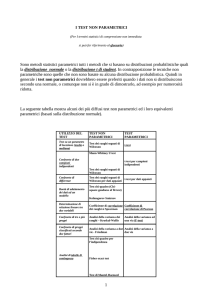
La tabella che segue riporta i principali test insieme con l'indicazione della loro natura, della
situazione sperimentale in cui sono utilizzabili e della PROC SAS e della opzione nel suo
ambito per richiedere la loro esecuzione.
9 Confronto tra due o più popolazioni attraverso tests non parametrici
218
Nota sull’Analisi .....(2a ed.)
Popolazioni
a confronto
Tipo di
randomizz.
Natura
del test
Nome del
test
PROC SAS / OPZIONE
2
2
completa
completa
mediane
ranghi
NPAR1WAY/MEDIAN
2 o più
2 o più
2 o più
completa
completa
blocchi
mediane
ranghi
ranghi
Mood
Wilcoxon;
Mann-Whitney
Brown & Mood
Kruskal & Wallis
Friedman
9 Confronto tra due o più popolazioni attraverso tests non parametrici
“
/WILCOXON
“
/MEDIAN
"
/WILCOXON
FREQ/CMH in TABLES
219
Nota sull’Analisi .....(2a ed.)
9.1 Test di Kruskal e Wallis
Sono messe a confronto le altezze degli alberi di tre tipi di foresta. I dati potrebbero in effetti
essere analizzati anche tramite l'analisi della varianza e servono solo da esemplificazione per
l'uso della PROC considerata.
PROGRAMMA SAS
Il test è eseguito tramite l'opzione WILCOXON nell'ambito della PROC NPAR1WAY. Si
indica in CLASS il criterio di classificazione ed in VAR la variabile di risposta in base alla
quale calcolare i ranghi.
*
* 9.1 TEST DI KRUSKAL E WALLIS
*
DAGNELIE (1975) - PAG. 391
*;
DATA esempio;
INPUT foresta altezza @@;
CARDS;
1 23.4
2 22.5 3 18.9
1 24.4
2 22.9 3 21.1
1 24.6
2 23.7 3 21.2
1 24.9
2 24.0 3 22.1
1 25.0
2 24.4 3 22.5
1 26.2
2 24.5 3 23.6
1 26.3
2 25.3 3 24.5
1 26.8
2 26.0 3 24.6
1 26.8
2 26.2 3 26.2
1 26.9
2 26.4 3 26.7
1 27.0
2 26.7
1 27.6
2 26.9
1 27.7
2 27.4
2 28.5
;
PROC NPAR1WAY WILCOXON;
TITLE '9.1 test di Kruskal e Wallis';
CLASS foresta;
VAR altezza;
RUN;
OUTPUT SAS
L'output fornisce fra l'altro, per ciascun livello del criterio di classificazione, la somma dei
ranghi osservata e quella attesa nell'ipotesi nulla di campioni estratti da una stessa popolazione
statistica. Il test χ2 permette di respingere l'ipotesi nulla con una probabilità di errore P ≤ 0.01
Ê.
9 Confronto tra due o più popolazioni attraverso tests non parametrici
220
Nota sull’Analisi .....(2a ed.)
9.1 test di Kruskal e Wallis
N P A R 1 W A Y
P R O C E D U R E
Wilcoxon Scores (Rank Sums) for Variable ALTEZZA
Classified by Variable FORESTA
FORESTA
1
2
3
N
13
14
10
Sum of
Scores
Expected
Under H0
Std Dev
Under H0
Mean
Score
316.500000
247.0 31.4119677
280.500000
266.0 31.9113943
106.000000
190.0 29.2213130
Average Scores were used for Ties
24.3461538
20.0357143
10.6000000
Kruskal-Wallis Test (Chi-Square Approximation)
CHISQ= 9.3337
DF= 2
Prob > CHISQ=
0.0094 Ê
9 Confronto tra due o più popolazioni attraverso tests non parametrici
221
Nota sull’Analisi .....(2a ed.)
9.2 Test di Friedman
Si riprende i dati già esaminati in 4.3 e si sottopone al test la variabile di risposta originale.
PROGRAMMA SAS
Il calcolo dei ranghi dei trattamenti nell'ambito di ciascun blocco è ottenuto con la PROC
RANK e la sua istruzione BY blocco, con l'istruzione VAR indicante la variabile di risposta. La
procedura sostituisce i valori originali della variabile "ninfes" con quelli dei ranghi. La PROC
SORT che precede dispone come al solito le osservazioni nell'ordine richiesto per l'esecuzione
della successiva PROC statistica implicante una istruzione BY.
L'esecuzione del test di Friedman può essere richiesta nell'ambito della PROC FREQ
richiedendo come opzione nell'istruzione TABLES, che riporta i due criteri di classificazione e
la variabile di risposta nell'ordine descritto, la statistica di Cochran-Mantel-Haenszel.
*
* 9.2 TEST DI FRIEDMAN
*;
DATA esempio;
INPUT tratt blocco ninfes @@;
CARDS;
1 1 40
1 2 48
1 3 16
1 4
2 1 8
2 2 7
2 3 18
2 4
3 1 5
3 2 11
3 3 25
3 4
4 1 13
4 2 9
4 3 36
4 4
5 1 6
5 2 16
5 3 10
5 4
6 1 3
6 2 6
6 3 20
6 4
7 1 26
7 2 20
7 3 6
7 4
8 1 6
8 2 20
8 3 7
8 4
9 1 2
9 2 3
9 3 12
9 4
;
PROC SORT;
BY blocco;
PROC RANK;
BY blocco;
VAR ninfes;
PROC FREQ;
TITLE '9.2 test di Friedman';
TABLES blocco*tratt*ninfes / NOPRINT
RUN;
18
26
7
37
0
18
21
10
0
CMH;
OUTPUT SAS
Il secondo test dell’output Ê equivale al test di Friedman ogni volta che, come in questo caso,
non si verifichino valori uguali della variabile di risposta per i trattamenti in ciascun blocco.
L'occorrenza di un numero limitato di tali uguaglianze altera comunque poco i risultati del test.
Come si nota, la minore potenza del test rispetto all'analisi della varianza eseguita in 4.3 sulla
variabile dipendente trasformata non consente in questo caso di respingere l'ipotesi nulla di
uguaglianza degli effetti dei trattamenti.
9 Confronto tra due o più popolazioni attraverso tests non parametrici
222
Nota sull’Analisi .....(2a ed.)
9.2
test di Friedman
SUMMARY STATISTICS FOR TRATT BY NINFES
CONTROLLING FOR BLOCCO
Cochran-Mantel-Haenszel Statistics (Based on Table Scores)
Statistic
Alternative Hypothesis
DF
Value
Prob
-------------------------------------------------------------1
Nonzero Correlation
1
5.886
0.015
2
Row Mean Scores Differ
8
12.538
0.129 Ê
3
General Association
96
105.298
0.243
Total Sample Size = 36
9 Confronto tra due o più popolazioni attraverso tests non parametrici
223